1.5 Опорные устройства и их реакции
Опорные устройства классифицируются по числу связей, накладываемых на перемещения опорных точек (узлов) конструкции. Связь обычно представляют в виде стержня, соединяющего конструкцию с опорной поверхностью. Если нет специального указания, опорные связи и поверхности считаются абсолютно жесткими. При нагружении конструкции со стороны опорных связей начинают действовать силы, называемые опорными реакциями. Опорные реакции находят из уравнений равновесия конструкции, у которого опорные связи мысленно удалены и заменены силами, направленными вдоль снятых связей. Для плоского бруса основными видами опор являются шарнирно-подвижная, шарнирно-неподвижная и защемленная неподвижная (рис. 1.5).
Шарнирно-подвижная, или, иначе катковая опора исключает перемещение опорного узла в направлении перпендикулярном опорной поверхности, но не препятствует вращению конструкции вокруг опорной точки и поступательному перемещению параллельно опорной поверхности. Такой опоре соответствует одна опорная реакция, направленная перпендикулярно опорной поверхности (рис. 1.5а).
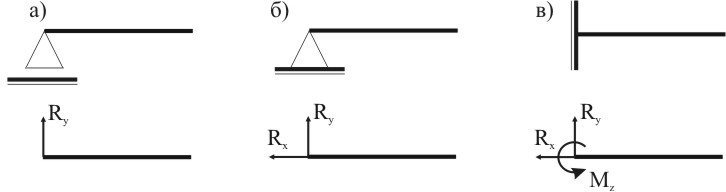
Рисунок 1.5
Шарнирно-неподвижная, или, короче, шарнирная опора исключает всякое поступательное движение опорного узла, но не препятствует вращению конструкции вокруг опорной точки. Реакцию такой опоры, направление которой заранее неизвестно, принято раскладывать на две составляющие Rx и Ry, направленные по касательной и нормами к опорной поверхности (рис. 1.5б).
Защемленная неподвижная опора, или, иначе, “заделка” исключает поступательные и вращательные движения конструкции. В соответствии с тремя связями, накладываемыми на конструкции, реакциями заделки являются силы Rx и Ry и опорный момент Mz (рис. 1.5в).
1.6. Основные допущения о свойствах материалов и допущения, связанные с характером деформаций
1. Гипотеза сплошности и однородности материала. Предполагают, что материал полностью заполняет весь объем конструкции, без каких либо пустот, и свойства материала не зависят от величины выделенного из конструкции объема. Гипотеза позволяет использовать методы анализа бесконечно малых величин (дифференциальное и интегральное исчисление).
2. Гипотеза изотропности. Материал конструкции изотропен, т.е. физико-механические свойства материала во всех направлениях одинаковы. Материал, не обладающий указанным свойством, называют анизотропным. Анизотропно - дерево, бумага, фанера, стальной прокат.
3. Гипотеза идеальной упругости. До определенных пределов нагружения материал конструкции является идеально упругим. Это справедливо при нормальных деформациях. При больших деформациях все материалы перестают обладать этим свойством, а потому данная гипотеза становится неприемлемой.
4. Гипотеза малости деформаций. Перемещения, возникающие в упругой конструкции под воздействием внешних нагрузок, малы по сравнению с его размерами. Эта гипотеза позволяет при составлении уравнений равновесия не учитывать изменения в расположении сил при деформировании конструкции (рис.1.6). Момент от силы P относительно заделки считается равным Pl, а не Pl1 , так как различие между l и l1 незначительно.
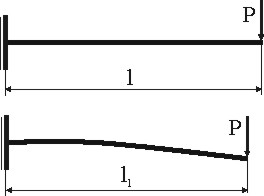
Рисунок 1.6
5. Гипотеза линейности перемещений. Перемещения точек упругой конструкции прямо пропорциональны действующим нагрузкам. Суть допущения рассмотрим на примере (рис. 1.7).
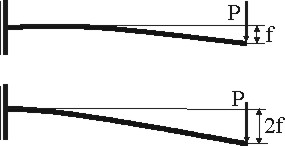
Рисунок 1.7
Если балка при действии силы P прогнется на величину f, то вдвое большая сила 2P вызовет прогиб в два раза больший 2f. Конструкции, для которых справедлива приведенная гипотеза, называют линейно деформируемыми.
6. Принцип независимости действия сил. Результат действия на конструкцию системы сил не зависит от порядка приложения внешних сил и равен сумме результатов действия каждой силы в отдельности.
Рассмотрим пример.
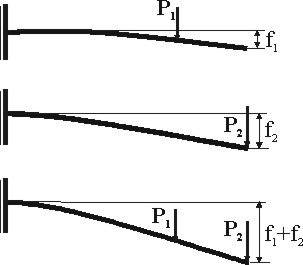
Рисунок 1.8
Если на балку (рис. 1.8) действует две силы P1 и P2, то точка А получит перемещение f. Если к балке приложить силу P1, точка А получит перемещение f1, при действии силы P2‑перемещение f2 .Перемещение f от одновременного действия двух сил P1 и P2 равно сумме перемещений f1 и f2, т.е. f=f1 + f2 . Этот принцип называют принципом суперпозиции, и он справедлив лишь для линейно деформируемых конструкций.
Следствие 1. Результат действия на тело нескольких сил равен сумме результатов отдельного действия каждой силы.
Следствие 2. Результат действия на тело нескольких сил не зависит от последовательности приложения этих сил.
7. Гипотеза плоских сечений (гипотеза Бернули). Сечения плоские и перпендикулярные к оси элемента конструкции до деформации, остаются плоскими и перпендикулярными к оси после деформации.
8. Принцип Сен-Венана. Особенности приложения внешних сил к конструкции проявляются, как правило, на расстояниях, не превышающих характерных размеров поперечного сечения. Деформации и напряжения в конструкции на большом расстоянии от места приложения сил по сравнению с характерными размерами поперечного сечения конструкции, на которую действуют силы, не зависят от распределения сил. От распределения сил зависят лишь местные деформации и напряжения в близко расположенных точках. Это значит, что при изучении распределения напряжений в конструкции достаточно принимать во внимание только равнодействующую внешних нагрузок, не интересуясь особенностями приложения нагрузки.
На рисунке 1.9 представлена иллюстрация принципа Сен-Венана на простейшем примере.
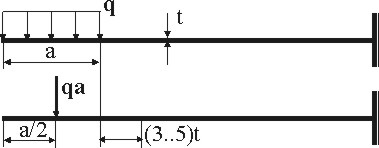
Рисунок 1.9
В соответствии с принципом Сен-Венана замена распределенной нагрузки статически эквивалентной сосредоточенной силой не окажет существенного влияния на условия нагружения части бруса, удаленной на расстояние не менее (3,5) t от правой границы действия распределенной нагрузки, где t‑ наибольший размер поперечного сечения бруса.