Раздел 8 Коэффициент интенсивности напряжений

Предельным случаем концентратора напряжений является трещина, которая математически представляет собой разрез «нулевой» ширины. Рассмотрим сквозную трещину длиной 2a в бесконечной пластине, которая находится под действием растягивающего напряжения  (рис. 3.108).

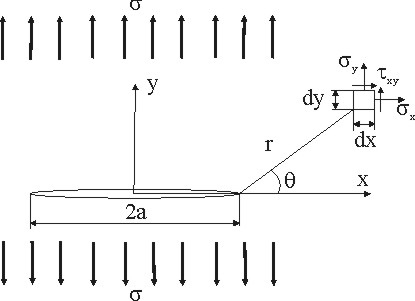
Рисунок 3.108

На гранях бесконечно малого элемента dxdy, находящегося на расстоянии r от вершины и составляющего с плоскостью трещины угол , возникают нормальные напряжения _x и _y касательные напряжения τ_xy. Методами теории упругости получено, что в случае плоского напряженного состояния напряжения в окрестности вершины трещины равны:

,

,

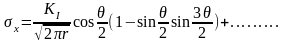_z= (_x+_y),

,

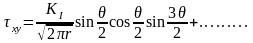Следует отметить, что все формулы имеют схожую структуру:

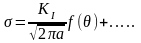
Приведенные соотношения содержат величину называемую коэффициентом интенсивности напряжений для трещины нормального разрыва. Этот коэффициент играет исключительную роль в механике хрупкого разрушения. Вблизи вершины трещины поле напряжений полностью зависит только от коэффициента интенсивности напряжений, который определяется внешними нагрузками и геометрическими размерами. Распределение же напряжений по угловой и радиальной координатам всегда одинаково.

Для вычисления коэффициентов интенсивности напряжений для элементов конструкции сложной конфигурации с трещинами, приходится решать задачи механики деформируемого тела для областей с разрезами (трещинами), решение которых связано с известными математическими трудностями вследствие наличия особых (сингулярных) точек. Большинство этих задач эффективно может быть решено только с применением ЭВМ.

Коэффициенты интенсивности обычно представляют в виде:

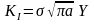
В механике разрушения безразмерный множитель Y носит название «К-тарировки». Он зависит от отношений длины трещины a к характерному размеру, например, для пластины к её ширине b, т.е. от числа =a/b.

Рассмотрим, как изменяется безразмерный множитель Y для наиболее часто используемых в практике схем нагружения.

Для пластины шириной b, растянутой постоянным напряжением , при эксцентрично расположенной трещине безразмерный множитель Y можно определить по графику, приведенному на рисунке 3.109. На рисунке приведены зависимости множителя Y от отношения длины трещины к ширине пластины a/b для различных соотношений d/b. Зависимости приведены как для вершины трещины у края пластины (точка A) так и для удаленной от края вершины (точка B).

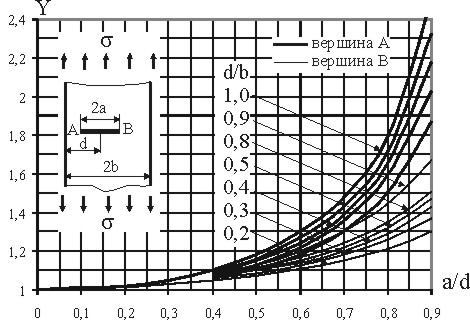
Рисунок 3.109

Из рассмотрения графика можно заметить, что множитель Y, а, следовательно, коэффициент интенсивности напряжений у вершины, которая ближе краю панели, выше, чем у противоположной вершины. По мере приближения вершины трещины к краю панели коэффициент интенсивности напряжений возрастает.

Повышенный уровень концентрации, вызванный отверстием в панели, часто приводит к образованию усталостной трещины. Трещину в панели от отверстия можно схематизировать односторонним или двусторонним разрезами от контура отверстия радиуса r в пластине бесконечных размеров подверженной двустороннему растяжению напряжением  и в перпендикулярном направлении напряжением α. Напряжение  действует в направлении перпендикулярном разрезу. Длина разреза, включая диаметр отверстия, равна 2a. Зависимости множителя Y от отношения полудлины трещины к радиусу отверстия a/r для односторонней и двухсторонней трещин приведены на рисунке 3.110.

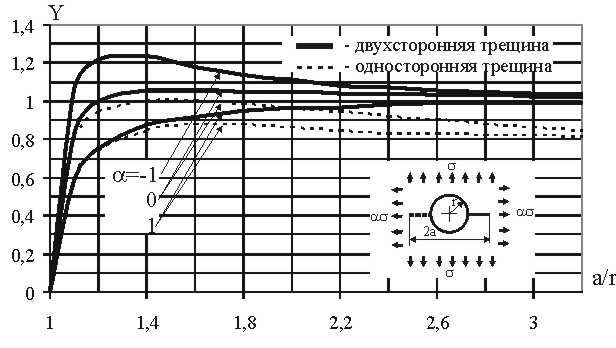
Рисунок 3.110

Из рисунка видно, что наибольшей величины множитель Y достигает для двухсторонней трещины длиной a от отверстия в том случае, когда перпендикулярно трещине действуют растягивающие напряжения , а вдоль трещины сжимающие напряжения той же величины.

Представляет практический интерес случай, когда трещина, развивающаяся в панели, приближается к отверстию. Этот случай схематизируют бесконечной пластиной с отверстием радиуса r и прорезью длиной 2a, середина которой отстоит от края отверстия на расстоянии b. Зависимости безразмерного коэффициента Y от отношения a/b для различных отношений расстояния от середины прорези до центра отверстия к радиусу отверстия c/r приведены на рисунке 3.111. Зависимости приведены для вершины трещины, которая расположена со стороны отверстия.

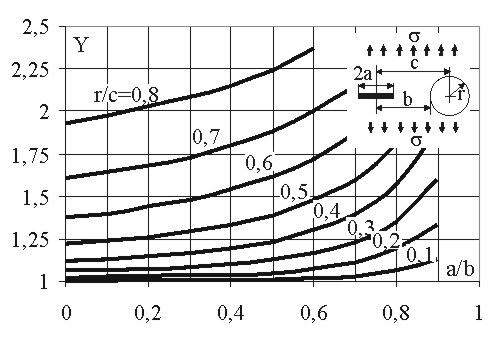
Рисунок 3.111

Можно заметить, что коэффициент интенсивности существенно возрастает по мере приближения вершины трещины к отверстию.

Панель крыла или фюзеляжа самолета представляет собой тонкостенную конструкцию, которая состоит из листа обшивки подкрепленной силовыми элементами. Трещину в такой панели можно схематизировать разрезом в листе, к которому точечно прикреплены жесткости, расположенные параллельно действующим напряжениям. Рассмотрим лист толщиной δ, к которому прикреплена серия параллельных жесткостей, расположенных на расстоянии b друг от друга и закрепленных к листу жестко в точках с шагом h. Разрез длиной 2a, имитирующий трещину, расположим под одной из жесткостей симметрично относительно её оси. На удалении от разреза к листу и подкрепляющим элементам приложим осевое растяжение напряжением  вдоль элементов жесткости. Для этого случая зависимости безразмерного коэффициента Y приведены на рисунке 3.112. Графики коэффициента Y приведены в зависимости от отношения a/b для различных значений параметра s, который является отношением жесткостей подкрепляющего элемента и листа, и вычисляют по формуле:

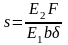, где

E₁, E₂- модули упругости листа и жесткости;

F- площадь поперечного сечения жесткости.

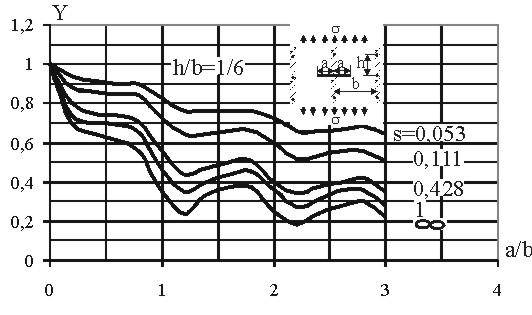
Рисунок 3.112

Из рассмотрения графиков можно отметить, что наличие жесткостей приводит к снижению коэффициента интенсивности по сравнению с тем случаем, когда жесткости отсутсвуют.