§ 7. Действия с непрерывными процентами
Непрерывное наращение процентов, то есть наращение за бесконечно малые отрезки времени, в практических финансово-кредитных операциях применяется крайне редко. Они используются, в основном, при анализе сложных финансовых проблем, например при обосновании и выборе инвестиционных проектов, при количественном финансово-экономическом анализе сложных хозяйственных процессов.
При непрерывном наращении процентов число периодов наращения или дисконтирования стремится к бесконечности, а временной интервал между периодами - к нулю.
Рассмотрим процесс наращения по сложным дискретным процентам:
и вычислим предел
при
:
так как
– второй замечательный предел.
Ставку непрерывных процентов называют
силой роста и обычно обозначают
через
,
чтобы отличать от дискретной ставки:
(21)
Если из (21) определить , то есть
то
будет дисконтным множителем.
Так как непрерывные и дискретные ставки функционально связаны между собой, то можно написать
то есть
,
Следовательно,
и
– (22)
связь между дискретными (сложными) и непрерывными процентами.
№ 30. Сумма, на которую начисляются
непрерывные проценты по ставке
,
равна 20000 руб. Найти наращенную за пять
лет сумму.
Решение.
32
тыс. 977,44 руб.
Проверим это решение по формуле (22):
,
или 10,51709%.
Тогда действительно:
32
тыс. 977,44 руб.
Если сила роста
не является постоянной величиной, а
изменяется во времени:
,
то наращенная сумма и современная
стоимость определяются как
(23)
Г Л А В А III
К О Н В Е Р С И Я П Л А Т Е Ж Е Й. Э К В И В А Л Е Н Т Н О С Т Ь П Р О Ц Е Н Т Н Ы Х С Т А В О К
§ 1. Финансовая эквивалентность обязательств
На практике нередко возникают случаи, когда необходимо заменить одно финансовое обязательство другим, например с более отдаленным сроком платежа; досрочно погасить задолженность; объединить несколько платежей в один (консолидировать платежи) и так далее.
В таких случаях неизбежно возникает вопрос о принципе, на котором должно базироваться изменение контракта. Таким общепринятым принципом является финансовая эквивалентность обязательств, которая предполагает неизменность финансовых отношений сторон до и после изменения условий контракта.
Эквивалентными считаются такие платежи, которые, будучи "приведены" к одному моменту времени, оказываются равными. Такое приведение осуществляется либо путем дисконтирования к более ранней дате; либо путем наращения суммы платежа, если речь идет о более поздней дате. По существу, принцип эквивалентности следует из формул наращения и дисконтирования, связывающих величины P и S, а именно, две суммы S1 и S2, выплачиваемые в разные моменты времени, считаются эквивалентными, если равны их современные (или наращенные) величины, рассчитанные по одной и той же процентной ставке на один и тот же момент времени.
№ 31. Являются ли эквивалентными два обязательства, если условия первого: выплатить 400 тыс. руб. через 4 месяца; второго: выплатить 450 тыс. руб. через 8 месяцев при условии начисления 20% годовых.
Решение. Применим формулу дисконтирования
Тогда
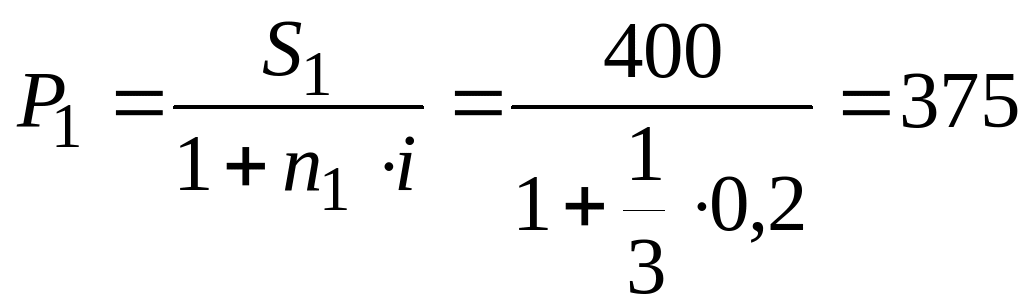тыс. руб.,
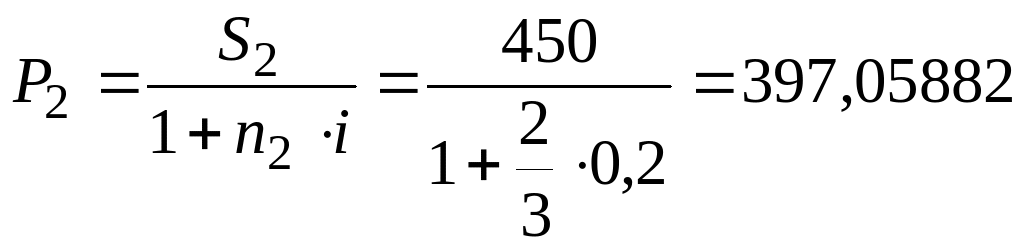тыс. руб.
Видно, что эти обязательства не являются
эквивалентными, так как
Очевидно, что результат сравнения S1
и S2 зависит от уровня
процентной ставки i
и существует (при данных
и
)
так называемый критический (или
барьерный) размер ставки
,
при которой обязательства будут
эквивалентными. Эту ставку можно
определить из равенства
или
Следовательно,
(1)
№ 32. Определить размер критической ставки в условиях № 31.
Решение.
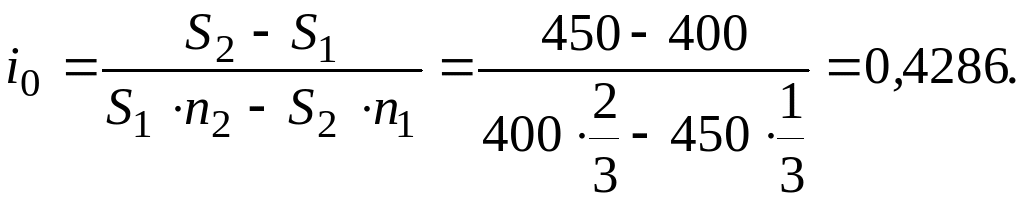
Таким образом, если
<
42,86%, то P2 > P1,
а если i > 42,86%, то
P2 < P1.
Если же дисконтирование будет производиться не по простой, а по сложной процентной ставке, то критическую ставку найдем из равенства:
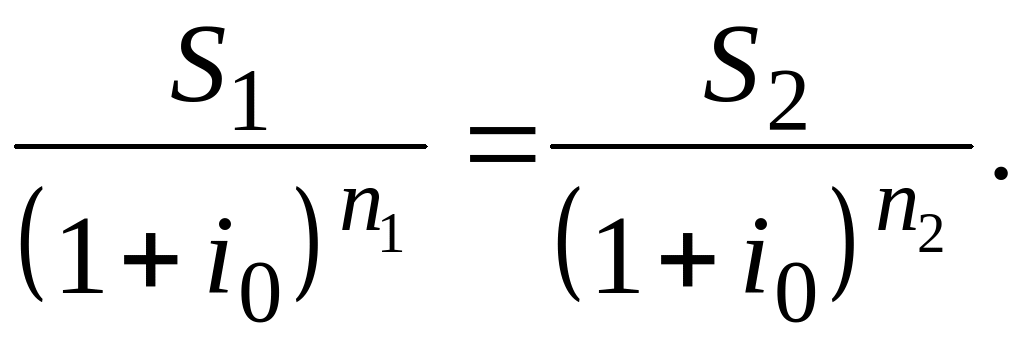
То есть
(2)
№ 33. Найти критическую ставку сложных процентов при сравнении двух платежей: 20 тыс. руб. с выплатой через два года и 30 тыс. руб. – через четыре года.
Решение.
или 22,47%.
Легко убедиться, что при i < i0 стоимость второго варианта больше первого, а при i > i0 – наоборот.