4.1.1. Управління смо на основі моделювання

Задача щодо оцінки і управління системою обслуговування вважається поставленою, якщо визначені такі її параметри: потік замов, що прибувають, структура системи і правила обслуговування замови (клієнта).

Потік заявок, що надходять, розглядається як випадковий процес і імовірнісний опис такого потоку повинен бути відомим до вирішення задачі теорії масового обслуговування (ТМО).

Математичний опис будь-якої системи починається із опису потоку замов, що надходять. Сутність теорії масового обслуговування витікає із того, що потік замов є простішим (Пауссоновським), тобто одночасно йому притаманні властивості стаціонарності, ординарності і відсутність послідовності. І в практичному використані найбільш розробленими в сенсі формального управління є такі СМО, де потік вимог є найпростішим. Тобто, частота надходження замов підпорядковується закону Пуассона, коли ймовірність надходження за час t дорівнює R вимогам.

Властивості найпростішого потоку: ординарність, стаціонарність і відсутність результату.

Ординарність – коли неможливе надходження одночасно 2 і більш заявок (вимог). Тобто ординарність віддзеркалює умови практичної неможливості надходження двох або більше заявок одночасно.

Стаціонарність означає незмінність ймовірнісного режиму потоку у часі. Імовірність надходження n заявок за проміжок часу (τ,τ+t), як ми пом'ятаємо, не залежить від розмірності τ, а залежить від величини проміжка. Тобто, ймовірність надходження вимог в перебігу заданого проміжку часу Δt залежить від його величини і не залежить від початку його відліку. Це потік, для якого математичне очікування числа заявок, що надходять в систему в одиницю часу (λ) не змінюється.

Хай ця імовірність – Р_n(t). Отримаємо , оскільки складаються ймовірності цілісної групи явищ.

Відсутність післядії означає, що кількість заявок, що надходять у систему після часу t не залежить від кількості, що надійшли в систему до цього часу .

Відсутність послідовності – число вимог до моменту t не визначає того скільки замовлень надійде в систему за час t+∆t.

Час обслуговування є випадковою величиною і описується за експоненційним законом розподілу: . Тобто імовірність того, що час обслуговування не перевершує деякої величини t (μ – параметр експоненційного закону часу обслуговування, тобто величина зворотня до середньому часу обслуговування - ).

Таким чином стаціонарний, ординарний потік можна характеризувати без наслідків вже відомою нам системою функції . Параметром найпростішого потоку є λ - інтенсивність потоку замов. Якщо середній час між надходженням двох замов означити – μ, то середня кількість замов, що надходить за одиницю часу буде – λ = 1/ μ.

При характеристиках черг вже зазначалось, що є СМО для яких характерні черги із вибуттям і без вибуття клієнтів.

Для прикладу розглянемо ситуацію для останнього випадку як найбільш поширеного. Хай на вході k – канальної СМО надходить простіший потік замов з інтенсивністю λ. Будемо вважати, що час обслуговування однієї замови є випадкова величина, що підкоряється закону розподілення - , де: υ – частість обслуговування; 1/ υ- середній час обслуговування однієї замови. Якщо приймемо, що в системі одночасно не може бути більше ніж m замов (m - найбільша кількість замов, що одночасно присутні в системі), то у якості критерію, що характеризує якісні властивості функціонування СМО можна вважати відношення середньої довжини черги до m. Таке відношення є коефіцієнтом простоювання обслуговуючого об’єкту. Якщо це описати на формальній мові моделювання, то для визначеного типу СМО слушні такі ймовірнісні характеристики [8]:

1. Ймовірність того, що зайнято k каналів обслуговування при умові, що кількість замов, які знаходяться в системі не перевищує кількості каналів

, 1<k<n, де: m – максимальна кількість замов, що присутні в системі одночасно; k – кількість каналів обслуговування; P₀ – ймовірність того, що канали вільні:

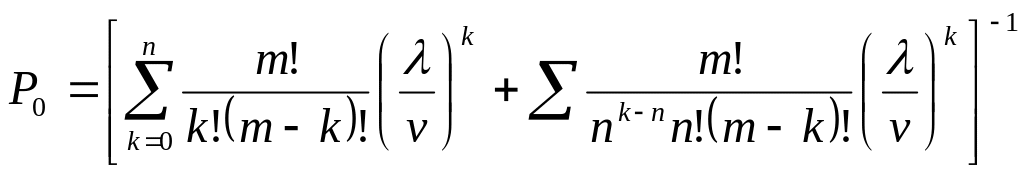
2. Ймовірність того, що в системі знаходиться k замов для випадку, коли їх кількість більша за кількість каналів - .

3. Середня кількість заявок, що очікують початку обслуговування (середня довжина черги):

4. Коефіцієнт простювання замов, що обслуговується: .

Алгоритм розрахунку розімкненої СМО. Імовірністний підхід

Якщо джерело надхоження потоку заявок має безкінцеву кількість вимог, то такі системи звуться розімкненими (магазин, каси вокзалів, каси портів і т.д.). Тобто для таких систем потік вимог, що надходять до системи вважається необмеженим. Розрахунок характеристик роботи таких систем здійснюється на підставі розрахунку імовірностей станів СМО (формули Ерланга). Оскільки розімкнені системи є типовими в операйійних системах (особливо в сфері сервісу) є сенс звернути на них додаткову увагу. Перш за все виділимо основні показники ефективності розімкнених СМО:

- імовірність того, що канали вільні або зайняті;

- математичне очікування довжини черги;

- коефіцієнт зайнятості і простоювання каналів обслуговування.

Нижче наведені моделі слід розглядати як доповнення до вище наведених ймовірнісних моделей стаціонарних систем.

Введемо параметр . Якщо - черга не може зростати безмежно, тобто число каналів, що обслуговують замовлення повинно бути більше середньої кількості каналів, необхідних для того що б за одиницю часу обслужити всі замовленння, що надходять. Якщо λ - середнє число замовлень, що надходять за одиницю часу; - середній час, що витрачається на обслуговування одним каналом одного замовлення, то в такому випадку - середнє число каналів, які необхідно мати, щоб обслужити у одиницю часу всі замовленння, що надійшли в цей час.

1. Імовірність того, що всі канали які здатні обслуговувати вільні:

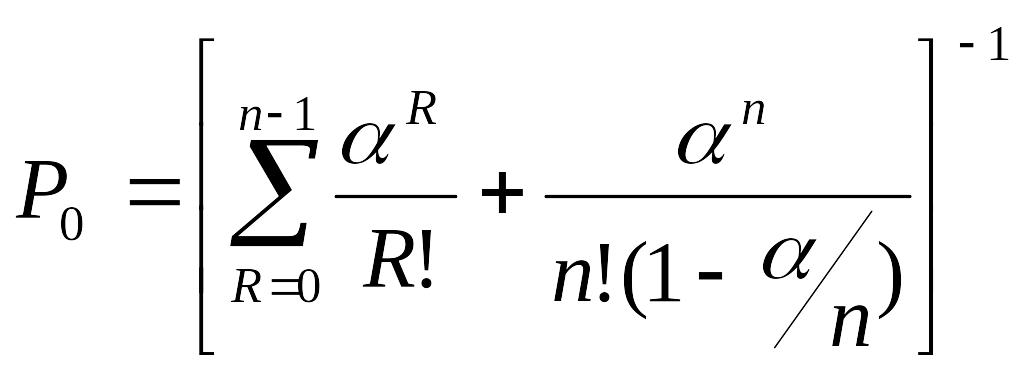
2. Імовірність того, що зайнято точно R каналів, за умови, що загальне число вимог, що знаходяться на обслуговуванні, не перевищує числа обслуговуючих апаратів: при 1≤ R≤ n.

3. Імовірність того, що в системі знаходитися R вимог, у випадку, коли їх кількість більша за число каналів, які обслуговують: при R ≥ n.

4. Імовірність того, то всі обслуговуючі канали зайняті: 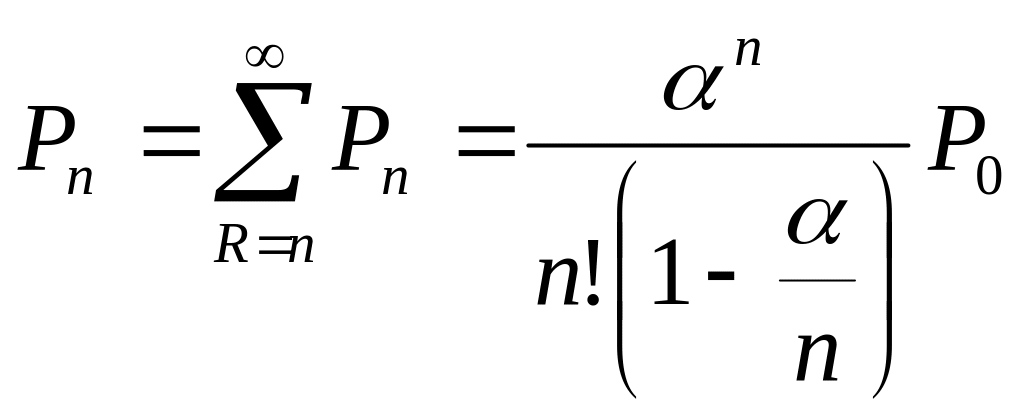при .

5. Середній час очікування вимоги початку обслуговування у системі: при ;

6. Середня довжина черги: 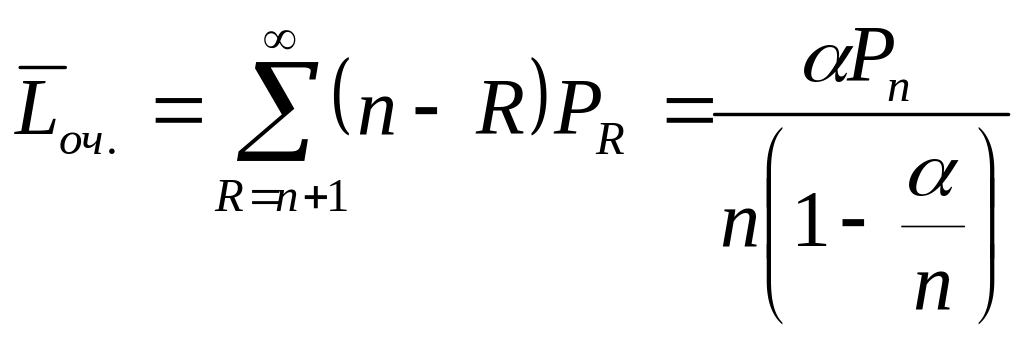при , або .

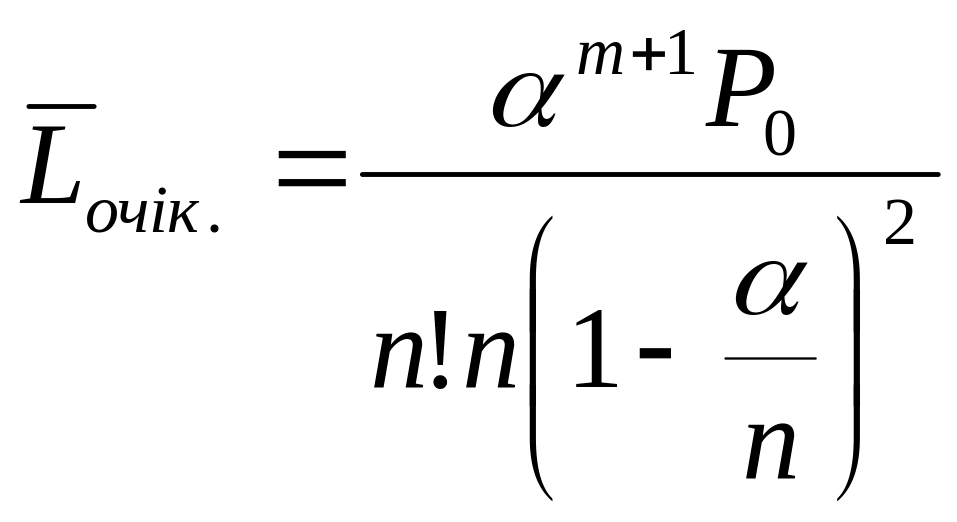7. Середнє число каналів, що вільні від обслуговування: .

8. Коефіцієнт простоювання каналів: .

9. Середня кількість каналів, що зайняті обслуговуванням:

10. Коефіцієнт завантаження каналів:

Означення в моделях:

R - зайнято каналів;

N – загальня кількість каналів ;

n – кількість клієнтів (замовлень);

α – інтенсивність надходження в систему замовлень;

μ – інтенсивність обслуговування;

L – довжина черги.

Приклад 4.1

Хай фірма що ремонтує електрообладнання має n = 5 майстрів. В середньому за день надходить λ=10 приладів. Потік випадковий (Пуассон). Час на ремонт також випадковий (характеристики поломок різні, кваліфікація майстрів різна). В середньому кожний з майстрів за день встигає відремонтувати μ = 2,5 прилад. Які характеристики фірми?

1. Визначимо параметр системи α; α = λ∙1/μ = 10∙1/2,5 = 4. Оскільки α ≤ n черга не може зростати безмежно. Фірма справляється з графіком ремонту.

2. Імовірність того, що всі майстри вільні від роботи:

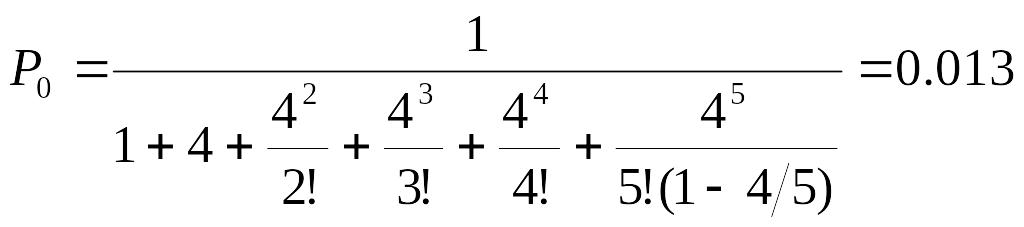
3.Імовірність того, що всі майстри зайняті: . Завантаження майстрів складає 55% часу.

4. Середній час обслуговування кожним каналом одного приладу (робочий день 7 годин): годин

5. Середній час очікування кожним несправним приладом початку ремонту: годин.

6. Середня довжина черги визначає місце для зберігання приладу:

7. Середнє число майстрів, що вільні від роботи:

Тобто, ремонтом в перебігу робочого дня зайнято 4 майстра із 5.

Імітаційна модель функціонування СМО

Найчастіше потік вимог і час обслуговування на практиці є випадковими величинами, тому характеристики функціонування СМО і рішення щодо операційного управління мають імовірнісний характер.

Процедури описування таких ситуацій не можна вважати простими, але для практичного уявлення є сенс розглянути спрощенний варіант появи черги на єдиній станції обслуговування. За мету будемо вважати визначення імовірності появи черги визначеної довжини і середньої довжина черги [7]. Вхідні і вихідні потоки замовлень – випадкові.

Приклад 4.2

Хай n – кількість замовлень в черзі до моменту t; P_n(t) – імовірність створення черги із n замовлень до моменту t; λ – середня швидкість появи замовлень, імовірність появи замовлень за одиницю часу; λ∆t – імовірність появи в черзі нової заявки у проміжку часу від t до t+∆t; μ – середня швидкість обслуговування; μ∆t – імовірність завершення обслуговування заяви від t до t+∆t; ñ – середня довжина черги.

Імовірність надходження або обслуговування більш ніж одного замовлення за ∆t вважається переважно малою, величина (∆t)² вважається дуже малою. За λ і μ треба визначити імовірність того, що до моменту t+∆t у черзі буде знаходитись рівно n заяв (n>0). Ця ситуація може бути надана як сума чотирьох складних незалежних подій, які виключні одне до одного.

1. До моменту t в черзі є n заяв, за ∆t немає надходжень замовлень і немає завершення обслуговування (імовірність цієї складної події Р_n(t) = (1- λ∆t)·(1- μ∆t)).

2. До моменту t в черзі є n+1 заяв, за ∆t немає надходжень замовлень, за ∆t закінчено обслуговування однієї заяви (імовірність цієї складної події Р_n+1(t)=(1-λ∆t)μ∆t)).

3. До моменту t в черзі є n-1 заяв, ще одне замовлення надійшло, на момент ∆t жодного замовлення не обслуговано (імовірність такої події Р_n-1(t) = λ∆t(1-μ∆t)).

4. До моменту t в черзі є n заяв, у продовж ∆t одна заява надійшла і одну заяву задовольнили (імовірність такої події Р_n(t) = (λ∆t)·(μ∆t)).

Нескладні перетворення (із врахуванням малості (∆t)² ) дають:

1. Р_n(t) × (1- λ∆t)×(1- μ∆t) = Р_n(t)×(1- λ∆t- μ∆t));

2. Р_n+1(t)×(1-λ∆t)×μ∆t)) = Р_n+1(t) ×μ∆t;

3. Р_n-1(t)×λ∆t(1-μ∆t) = Р_n-1(t)×λ∆t;

4. Р_n(t)×λ∆t×μ∆t = 0.

Для події, що нас цікавить результуюча імовірність дорівнює, у даному випадку, як сума описаних чотирьох імовірностей: Р_n(t+∆t) = Р_n(t) · (1- λ∆t- μ∆t+ Р_n+1(t)·μ∆t + Р_n-1(t)·λ∆t), або {Р_n(t+∆t) – P_n(t)} ∕ ∆t = λP_n-1(t) + μP_n+1(t) – (λ+μ)P_n(t). Крокуючи до межі при ∆t→ 0 отримаємо диференційне рівняння: dP_n(t)/dt = λP_n-1(t) + μP_n+1(t) – (λ+ μ)P_n(t) для n > 0. Потрібно також враховувати і випадок відсутності черги, тобто випадок n = 0. Таке може бути якщо :

• або черги немає і замовлення не з’явилось (імовірність такої події Р₀(t)(1 - λ∆t));

• або черга складалася із єдиного замовлення, яке було виконано і нових заявок не надходило (імовірність цієї події Р₁(t)μ∆t(1 - λ∆t)).

Оскільки ці дві складні події незалежні, то імовірність відсутності черги у момент t + ∆t дорівнює сумі наведених нерівностей: Р₀(t+∆t) = Р₀(t)(1 - λ∆t) + Р₁(t)μ∆t(1 - λ∆t) = Р₀(t) - Р₀(t) λ∆t) + Р₁(t)μ∆t або Р₀(1 + ∆t) – Р₀(t)/∆t = - λР₀(t) + μР₁(t), що веде при ∆t→ 0 до рівняння: dP₀(t)/dt = -λP₀(t) + μP₁(t).

Отримані рівняння вважаються досить складними, але якщо розглядати випадок dP_n/dt = 0, то отримаємо рівняння: 0 = λР_n-1+μP_n+1 – (λ+μ)P_n(n>0), 0 = -λP₀ + μP₁(n=0). Рішення цих рівнянь Р₀, Р_1,..., Р_n … можна знайти при природній вимозі λ∕μ < 1(інакше система не зможе обслужити потік заяв) _, виходячи з того, що .

Хай для n = 1 маємо Р₀, в такому випадку Р₁ = (λ/μ)Р₀. Для n =1 і знайденого Р₁ отримуємо Р₂ = (λ/μ)²Р₀ для n = 2 отримаємо Р₃ = (λ/μ)³Р₀ , тобто зрозуміло, що P_n = (λ/μ)ⁿР₀ . В такому разі , оскільки λ/μ < 1, то для безкінцево убиваючої геометричної прогресії маємо і Р₀ = 1 – (λ/μ). Тому отримаємо, що Р_n = (λ/μ)ⁿ(1-λ/μ)).

Такий спосіб (послідовне інтегрування і диференціювання) дозволяє знайти і середню довжину черги , λ/μ < 1. Залежність від (λ/μ) можна бачити із наступної таблиці:

λ∕μ	1/2	3/4	7/8	15/16	31/32	....
ñ	1	3	7	15	31	....

Знання того, яка довжина черги, які витрати на розширення можливості обслуговувати потік замовлень, які втрати через черги, дозволяє обрати переважний варіант обслуговуючої організації.

Використовуючи наведені моделі і вирішуючи їх за допомогою ЕОМ (розрахунки по кожному варіанту витрат, доходів, втрачену корисність), можна знайти переважний варіант планування і експлуатації систем обслуговування.

Прикладний аспект розрахунку характеристик СМО

Оскільки прикладний операційний менеджмент має справу із реальними одно і багатоканальними системами, наведемо спрощенний формалізований підхід до визначення характеристик СМО у декілька зміненій інтерпретації [2].

Якщо ввести символьні означення основних параметрів і процесів СМО:

А – середня частота надходження заявок (інтенсивність);

С – середня швидкість обслуговування на один сервісний канал;

N – кількість сервісних каналів;

Т – інтенсивність навантаження (трафік): Т=А/СN. Сервісні потужності повинні перевищувати попит – Т<1, то для одноканальної системи матимемо такі формалізми [2 ]:

1. Середня кількість покупців (замовлень) в черзі:

2. Середня кількість покупців (замов) в системі:

3. Середній час чекання у черзі:

4. Частка часу коли потужності простоюють: Q=1-T

5. Ймовірність того, що в системі n замов:

Для багатоканальній системи:

1. Ймовірність того, що в системі не буде покупців (замов): ;

2. Середня кількість замов в черзі: ;

3. Середня кількість замов в системі: ;

4. Середній час очікування в черзі:

5. Ймовірність, що всі замови будуть задоволені: .

У разі n=N будуть виконані всі замовлення, що знаходяться у черзі.

Оскільки є практичний сенс розглядати проекти станцій обслуговування, де 1/μ<1/λ , а в такому випадку через деякий час система переходить у стаціонарний режим функціонування, то якщо 1/μ означимо як ρ (навантаження системи), можна визначити, що стаціонарний режим настане при умові ρ< λ.

Тобто в залежності від значень λ, µ і ρ будемо мати стаціонарний - ( ), або не стаціонарний - ( ; ) режим роботи системи.

В такому разі можна визначити важливі параметри функціонування системи [4]:

Е₁=1- ρ - коефіцієнт простоювання системи;

Е₂ = ρ/(1- ρ) – середня кількість клієнтів в системі;

Е₃ = ρ²/(1- ρ) – середня довжина черги;

Е₄ = 1/(μ-λ) – середній час знаходження клієнта у системі;

Е₅ = ρ /(μ-λ) – середній час коли клієнт перебуває в черзі.

Приклад 4.3

Фірма замовила проект автоматичної заправочної станції (АЗС) з такими вхідними параметрами: інтервал між прибуттям автомобілів 4 хвилини, середній час обслуговування: 5; 3,5; 2; 1 та 0,5 хвилин. Розрахувати параметри АЗС щодо черги та зробити вибір варіанту багатоканальної системи.

Рішення:

Спираючись на вище наведені формули визначимо характеристики СМО : завантаження; простоювання; наявність клієнтів в системі; довжина черги; час знаходження в черзі; час знаходження в систем. На цій основі створимо матрицю на 5 каналів обслуговування , розрахуємо основні характеристики кожного каналу обслуговування і визначимо кращий варіант (табл. 4.1).

Таблиця 4.1. Характеристики багатоканальної СМО

	1	2	3	4	5
	4	4	4	4	4
	0,25	0,25	0,25	0,25	0,25
	5	3,5	2	1	0,5
	0,2	0,28	0,5	1	2
	1,25	0,87	0,5	0,25	0,125
	-0,25	0,125	0,5	0,75	0,875
	-5	7	1	0,33	0,143
	-6,25	6,125	0,5	0,08	0,018
	-20	27,48	4	1,33	0,57
	-25	24,3	2	0,33	0,07

Зробимо аналіз наведених в таблиці результатів:

a). 1-й варіант не підходить, оскільки черга ∞;

b). 2-й варіант гарний за показниками завантаження – ρ = 0,87 та малим часом простоювання Е₁= 0,125, проте збільшена черга і середній час простою Е₄ = 27 хвилин;

c). 3-й варіант: обладнання простоює 0,5 (ρ); кількість авто в системі = 1(Е₂), а середні втрати часу = 4 (Е₄) при середньому часі обслуговування = 2 хвилини;

d). У варіантах 4 та 5 черги немає, проте обладнання простоює тривалий час.

Слід звернути увагу на 3 – й варіант з урахуванням тенденції зростання кількості автомобілів в країні.

Остаточний вибір залишається за фірмою-замовником.