4. Системы линейных уравнений

4.1. Определения.

Пусть P – некоторое поле.

Системой m линейных уравнений с п неизвестными называется система уравнений вида:

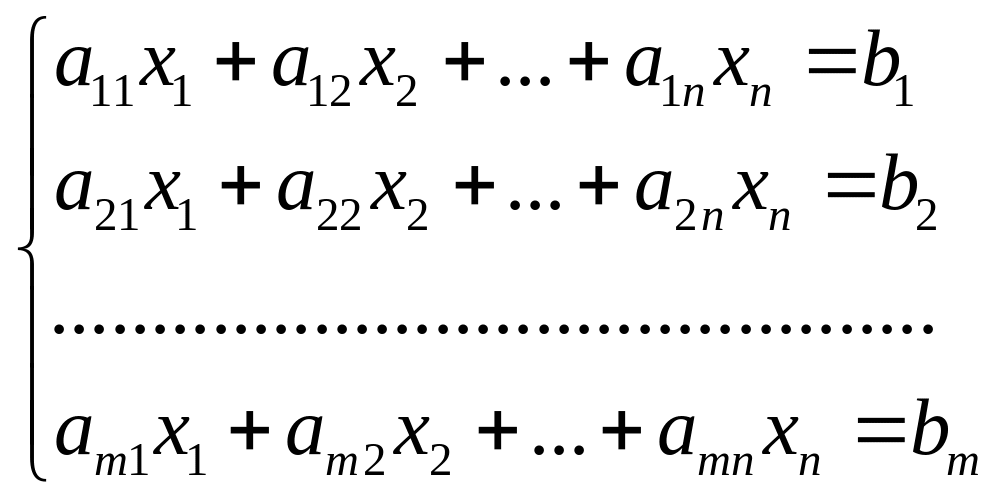, (4.1)

где все a_ij , b_i  P.

Для простоты такую систему мы будем записывать таблицей вида:

Такая таблица называется расширенной матрицей системы линейных уравнений. Матрица

A =

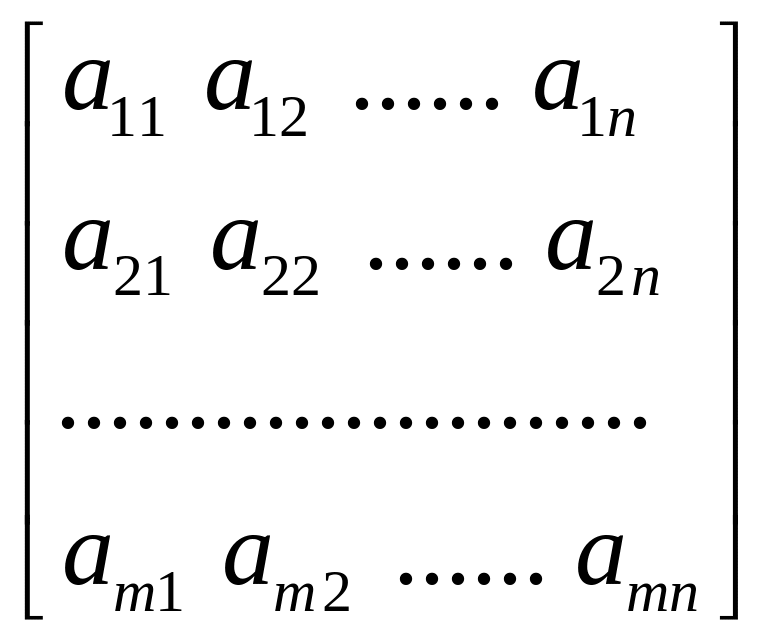
называется основной матрицей системы. Сокращенно систему линейных уравнений будем называть СЛУ. Очевидно, по расширенной матрице СЛУ восстанавливается однозначно.

Решением системы линейных уравнений называется такой набор (с₁,…,с_n) элементов из P, что при подстановке в систему х₁ = с₁, … , х_п = с_n получаются верные равенства:

a₁₁ с₁ + … + a_1n с_n = b₁, a₂₁ с₁ + … + a_2n с_n = b₂, …

Если у системы имеются решения, то она называется совместной. Если у системы нет решений, то она называется несовместной. Если у системы имеется единственное решение (с₁,…,с_n), то она называется определенной. Если у системы имеется более одного решения, то она называется неопределенной.

Определим для строчек с элементами из поля Р операции так: (a₁,…, a_n)+ (b₁,…,b_n) = (a₁ + b₁, …, a_n + b_n) – сложение строчек, и с(a₁,…,a_n)= (сa₁,…,сa_n) – умножение строчки на элемент с Р.

Такие операции мы будем проделывать со строчками расширенной матрицы СЛУ. Очевидно, сумме строчек расширенной матрицы соответствует сумма соответствующих уравнений системы, а умножению строчки на элемент с Р соответствует умножение соответствующего уравнения на с.

Будем говорить, что система S является следствием системы S, если любое решение системы S является решением системы S. Обозначать этот факт будем так: S  S. Будем говорить, что системы S и S равносильны, если S  S и S  S. Записывать это будем так: S  S. Другими словами, S  S тогда и только тогда, когда множества решений систем S и S совпадают.

Утверждение. Отношение равносильности  на множестве систем линейных уравнений с п неизвестными является отношением эквивалентности.

Доказательство очевидно.

Следовательно, множество систем линейных уравнений разбивается на классы эквивалентных. Для решения произвольной СЛУ было бы удобно найти в классе эквивалентных ей систем наиболее простую систему и найти все решения этой наиболее простой системы. Это множество решений будет совпадать с множеством решений первоначальной СЛУ. Далее мы и будем искать наиболее простые системы среди систем, эквивалентных данной.

4.2. Элементарные преобразования.

Будем делать над системами линейных уравнений элементарные преобразования трёх типов.

Будем говорить, что СЛУ S получается из системы S элементарным преобразованием I-го типа (S S ), если i-е уравнение системы S получается прибавлением к i-му уравнению системы S j-го уравнения системы S, умноженного на коэффициент с  Р (j i). А все остальные уравнения системы S совпадают с соответствующими уравнениями системы S. Элементарному преобразованию I-го типа системы линейных уравнений соответствует ЭП-I соответствующей расширенной матрицы, у которой при ЭП-I к i-й строке прибавляется j-я строка с коэффициентом с. Таким образом, все строки расширенной матрицы для СЛУ S, кроме i-й, совпадают с соответствующими строками расширенной матрицы для СЛУ S, а i-я строка имеет вид

(a_i1+ca_j1, a_i2+ca_j2,…, a_in+ca_jn,| b_i+cb_j).

При элементарном преобразовании II-го типа в системе S меняются местами i-е и j-е уравнения, а в соответствующей расширенной матрице меняются местами i-я и j-я строки.

При элементарном преобразовании III-го типа в системе S i-е уравнение умножается на коэффициент с Р, с  0, а в соответствующей расширенной матрице i-я строка умножается на с.

Упражнения.

1. Доказать, что если S S , то S S , причем обратное ЭП - того же типа.

2. Доказать, что если S S , то S  S и, следовательно, S  S .

На множестве СЛУ с п неизвестными введем отношение  . Пусть по определению S  S, если система S может быть получена из S с помощью цепочки ЭП: S … S .

Упражнения.

3. Доказать, что отношение  является отношением эквивалентности.

4. Доказать, что если S  S, то S  S, и, следовательно, отношение эквивалентности  содержится в отношении эквивалентности  .

Теорема. Любую матрицу размером mn

A =

c помощью ЭП можно привести к ступенчатому виду:

= ,

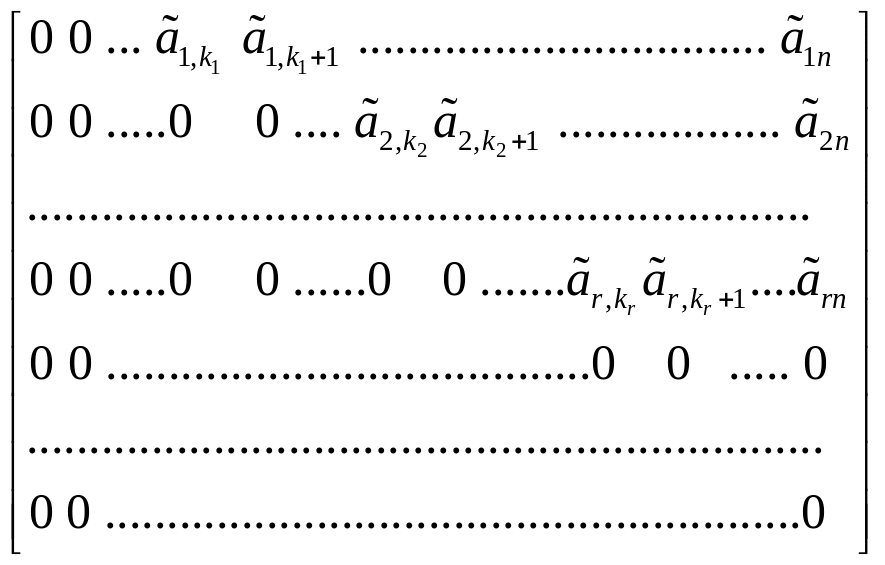где число ненулевых строк равно r, r 0, и все элементы  0, i = 1,…,r.

Доказательство индукцией по m.

При m = 1 утверждение очевидно и ничего доказывать не надо.

Пусть для m – 1 утверждение верно. Докажем его для m. Пусть в 1-м столбце все элементы нулевые, во 2-м столбце все элементы нулевые и т.д. Пусть 1-й столбец, где встретится элемент, неравный нулю, имеет номер k₁ , k₁ 1. Строку, где находится этот ненулевой элемент, поменяем местами с 1-й строкой. Элемент, который окажется на месте с номером (1, k₁), обозначим , элемент, который окажется на месте с номером (1, j), обозначим , а элемент на произвольном

(i, j)-м месте (i  2) будем обозначать . Теперь с помощью ЭП-I сделаем нули под ненулевым элементом . Для этого от каждой строки с номером j, j  2, отнимем 1-ю строку с коэффициентом . После этого получим матрицу вида

.

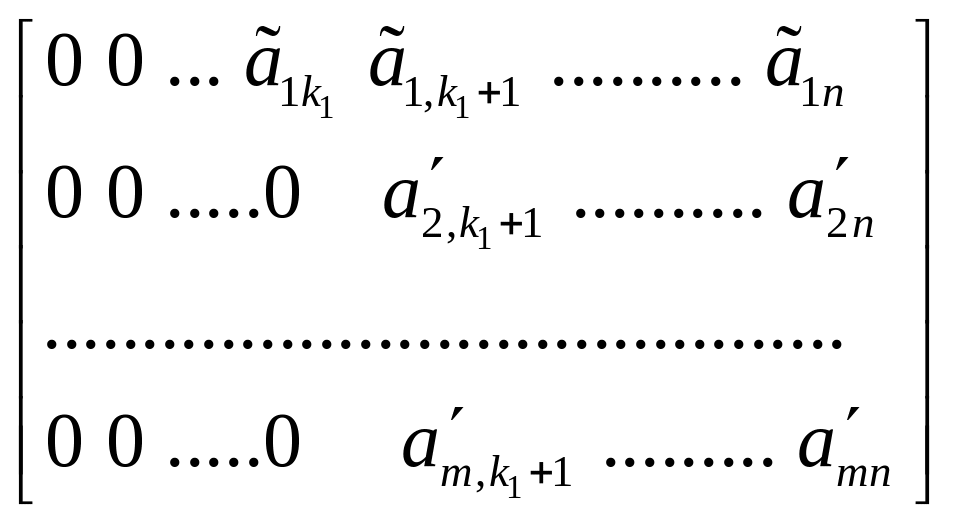Для подматрицы с m-1 строками

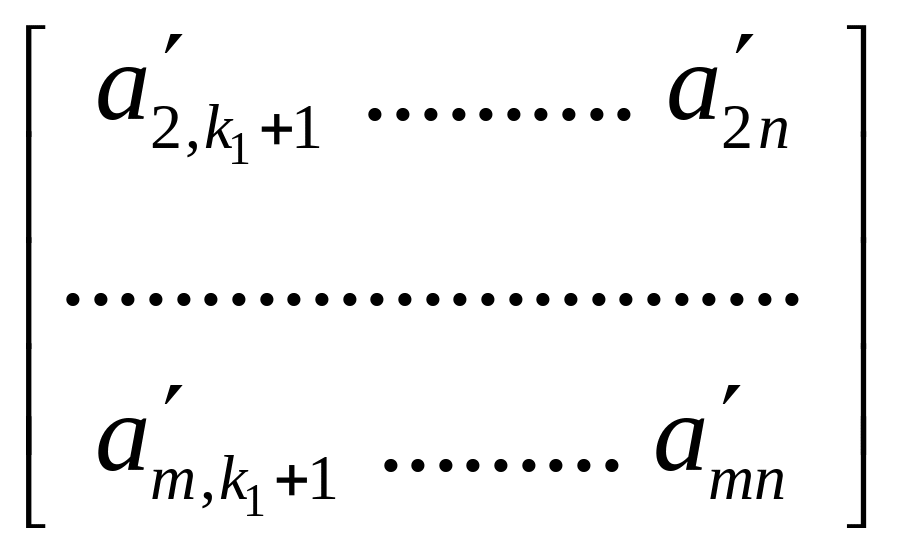
можно считать, что утверждение верно по предположению индукции. Отсюда и следует доказательство теоремы.



Число r ненулевых строк матрицы (число ступенек) называется рангом матрицы A и обозначается rgA. Корректность определения ранга (независимость от способа приведения A к ступенчатому виду) будет доказана позже.

Лекция 6.