6.5. Поля.

Примеры числовых полей хорошо известны – это

Q,+,  , -( ), 0 , 1 , R,+,  , -( ), 0 , 1 , C,+,  , -( ), 0 , 1 .

Также мы доказали, что  простого числа p  Z полем яв­ляется  Z_p ,+,  , -( ), , .

Определение. Если P = P, +, , -( ), 0_K , 1_K  - поле,

F P и F = F,+, , -( ), 0_K , 1_K  - поле, то F называют подполем поля P, а P называют надполем поля F или расширением поля F. Если ясно, какие операции имеются в виду, то говорят, что F – подполе поля P, а P – расширение поля F.

Определение. Если Р₁, Р₂ – поля, то отображение

: Р₁ Р₂ называется изоморфизмом полей, если  - биекция, и  x,y Р₁ (x+y) =  x + y, (xy) =  x  y. Если для полей Р₁ и Р₂ такой изоморфизм существует, то говорят, что поля Р₁ и Р₂ изоморфны и пишут Р₁  Р₂.

Упражнения.

1. Доказать, что id: Р₁ Р₁ является изоморфизмом, то есть Р₁  Р₁.

2. Доказать, что если :Р₁Р₂ – изоморфизм, то  ^-1:Р₁Р₂ – изоморфизм, то есть если Р₁  Р₂, то Р₂  Р₁.

3. Доказать, что если :Р₁ Р₂ , :Р₂ Р₃ – изоморфизмы,

то  ◦:Р₁ Р₃ – изоморфизм, то есть если Р₁  Р₂ и Р₂  Р₃ , то Р₁  Р₃.

4. Доказать, что если :Р₁ Р₂ – изоморфизм, то

(0 )=(0 ), (1 )=(1 ),(-х)= - х хР₁,

(х ^-1)= ( х)^-1 х Р₁, х  0 .

Пусть P - поле. Будем обозначать элементы вида

ab^-1 = b^-1a дробями . Тогда =  ab^-1 = cd ^-1

ad = bc, + = ab^-1+cd ^-1 =( ab^-1+cd ^-1)bd( bd) ^-1 =

= (ad + bc)( bd) ^-1= ,  = ab^-1cd ^-1 =ac(bd) ^-1= .

Любое поле P содержит элементы 0_Р, 1_Р, 1_Р + 1_Р = 2(1_Р), 1_Р + 1_Р +1_Р =3(1_Р),…, m(1_Р) m  N. Возможны два случая:

1) все элементы вида m(1_Р), m  N, различны.

2) среди этих элементов  одинаковые, то есть в N  m  n : m(1_Р)= n(1_Р) (такой случай имеет место всегда для конечного поля Р). Пусть m  n. Тогда (m – n)(1_Р)= 0_Р , то есть существует такое t  N, что t(1_Р)= 0_Р .

Определение. Характеристикой поля Р называется наименьшее натуральное число t такое, что t(1_Р)= 0_Р . Если такого числа не существует (как в случае 1), то говорят, что характеристика поля равна 0 или ∞ . Характеристика поля обозначается через char P.

Очевидно, char Q = char R = char C = 0, char Z_p = p.

Теорема. Если р = char P  0, то р – простое число.

Доказательство. Пусть р – не простое, p = kl, где k, l  1.

Тогда 0_Р = p(1_Р)= (kl)(1_Р) = k(1_Р) l(1_Р), и k(1_Р)  0_Р, l(1_Р)  0_Р. Но в поле нет делителей нуля (см. 6.3), то есть мы получили противоречие. Значит, р – простое число.



Определение. Поле Р называется простым, если у него нет подполей, отличных от Р.

Теорема. Поле Q – простое.

Доказательство. Пусть Q  Р – подполе. Тогда Р  0, 1, 1+1=2, 2+1=3,…, n (n  N), - n (n  N),  (n  N), m (n  N, m  Z), то есть Р  Q  Р = Q. Других подполей в Q нет.



Теорема. Поле Z_p – простое.

Доказательство. Пусть Z_p  Р – подполе. Тогда Р  , , + = , + = , … , , то есть Р  Z_p  Р = Z_p . Других подполей в Z_p нет.



Теорема. Пусть Р – поле, и char P = 0. Тогда

1. P содержит наименьшее (по включению) подполе Р₀ ,

2. подполе Р₀ – простое,

3. Р₀  Q.

Доказательство. Очевидно, пересечение всех подполей в Р является, во-первых, подполем, во-вторых, оно является наименьшим подполем (так как содержится в любом другом) и, в-третьих, оно является простым подполем, так как не содержит собственных (меньших) подполей. Отсюда следуют 1-е и 2-е утверждения теоремы.

Но мы докажем теорему иначе. Пусть поле P содержит под­поле Р₁. Тогда Р₁  0_Р, 1_Р, 1_Р+1_Р=2(1_Р), 2(1_Р)+1_Р =3(1_Р),…, n(1_Р) (n  N), (- n)(1_Р) (n  N), (n(1_Р))^{- 1} (n  N), m(1_Р)(n(1_Р))^{- 1} (n  N, m  Z). Пусть

Р₀={m(1_Р)(n(1_Р))^{- 1}| n N, m Z}= { | m Z, n N}. Тог­да Р₀ - подполе, так как

I. + =  Р₀ (*)

и =  Р₀  ,  Р₀ , (**)

II.2. при m = 0, n = 1 получаем, что 0_P  Р₀ ,

3. - =  Р₀ , 6. при m = 1, n = 1 получаем, что 1_P Р₀ , 7. при m  0 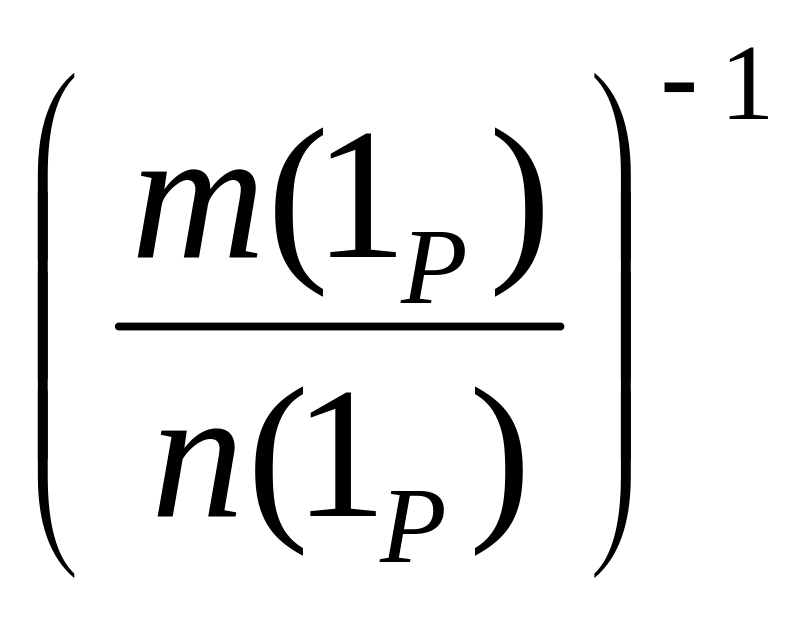=  Р₀ - при m  0 здесь используется правило знаков из 6.2. Выполнение остальных свойств из определения поля в Р₀ следует из выполнения их в поле Р.

Подполе Р₀ - наименьшее, так как любое другое подполе Р₁ содержит Р₀. Отсюда следует, что Р₀ - простое подполе, так как оно не содержит собственных (меньших) подполей.

Докажем, что поле Р₀ изоморфно полю Q. Определим отображение : Q  Р₀ так: пусть   Q по определению ( )=  Р₀ . Тогда  - инъекция. В самом деле, если ( )=( ), то =  m(1_Р)n(1_Р) =

= m(1_Р)n (1_Р)  (mn)(1_Р) =(mn)(1_Р) (mn - mn)(1_Р))=0_Р 

mn - mn = 0 (так как char P = 0)  = . Сюръективность  очевидна. Таким образом,  - биекция. Сохранение операций при  следует из (*) и (**). Следовательно,  - изоморфизм.



Теорема. Пусть Р – поле, и char P = р. Тогда

1) P содержит наименьшее (по включению) подполе Р₀ ,

2. подполе Р₀ – простое,

3. Р₀  Z_p.

Доказательство аналогично доказательству предыдущей теоремы 3.

Упражнение. Доказать эту теорему.

Лекция 13.