19.3. Структура ортогонального оператора.
Лемма. Пусть : Е Е - ортогональный оператор, Е L -
-инвариантное подпространство. Тогда L - -инвариантное
подпространство.
Доказательство. х L, y L ( x, y) = (x, y) = 0 (L) L . Но L = L (так как |L – ортогональный и невырожденный) (L) L (L) L (на самом деле, (L) = L, так как на L - ортогональный и невырожден-
ный).
Пусть : Еп Еп - ортогональный оператор. По теореме из п. 16.7 в Еп L1 - -инвариантное подпространство размерности 1 или 2. Тогда по лемме L1 - -инвариантное подпространство, и Еп = L1 L1. Так как на L1 - ортогональный оператор, то в L1 L2 - -инвариантное подпространство размерности 1 или 2, и ортогональное дополнение L к L2 в L1 также -инвариантно. Далее,
Еп = L1L2L, и в L L3 - -инвариантное подпространство размерности 1 или 2, и так далее. В конце концов, мы получим разложение Еп = L1L2…Lq , где все Li –
-инвариантны, попарно ортогональны, и можно считать, что dimL1 = dimL2 =…= dimLs = 2, dimLs+1 =…= dimLq = 1.
Если L – евклидово пространство размерности 1, L = <e>, и : L L - ортогональный оператор, то е = е,
( е, е) = (е,е) 2(е,е) = (е,е) 2=1, = 1 = id.
Если же L – евклидово пространство размерности 2,
L = <и1, и2>, где {и1, и2} – ортонормированный базис в L, и
: L L - ортогональный оператор, то | и1| = | и1| = 1 и1= cos и1+ sin и2 ; | и2|= | и2|=1, ( и2, и1)=(и2, и1)= = 0 и2 = (-sin и1 + cos и2).
a)
Если
и2=
-sin
и1+
cos
и2,
то [
]
=
,
и - поворот L на угол против часовой стрелки.
б) Если
и2=
sin
и1 -
cos
и2,
то [
]
=
,
и характеристический многочлен (t)=
t2
– 1. Для
собственных значений t1,2
= 1
два собственных вектора
е1,
е2
. Так как (
е1,
е2)=
(+е1,
- е2)=
(е1,
е2),
то (е1,
е2)
= 0,
е1
е2.
Пусть L
= <e1>,
L
= <e2>.
Тогда L
= L
L
- прямая
сумма одномерных взаимно ортогональных -инвариантных
подпространств таких, что |L = id, |L = - id.
В разложении Еп = L1L2…Lq выберем в каждом Li ортонормированный базис. Объединение и этих базисов является ортонормированным базисом в Еп. В этом базисе матрица ортогонального оператора имеет клеточно-диаго- нальный вид:
[
]
=
,
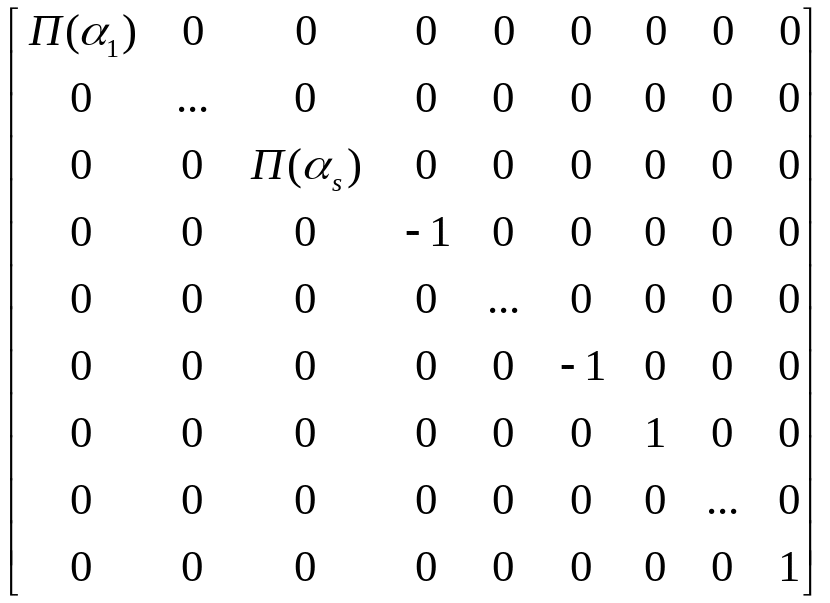где П(i)
=
.
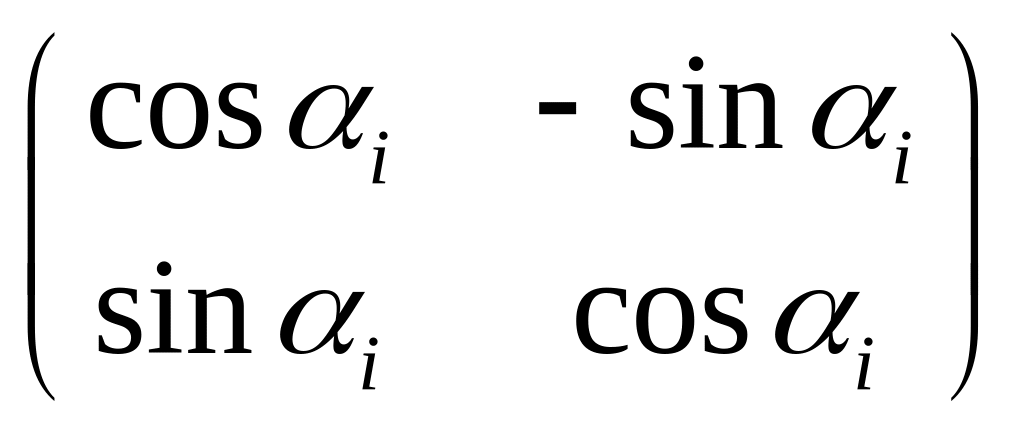Заметим, что
=
П(),
=
П(0).
Таким образом, нами доказана структурная
Теорема. Для любого ортогонального оператора
: Еп Еп ортонормированный базис и евклидова пространства, в котором матрица имеет вид:
[
]
=
.
(19.1)
В матрице -1 и 1 взяты в скобки, что означает, что эти элементы могут присутствовать, а могут и отсутствовать. Верно и обратное утверждение: если [ ] имеет вид (19.1), то -
ортогональный оператор.
На языке матриц теорему можно сформулировать так:
Для любой ортогональной матрицы А ортогональная матрица Т (матрица перехода к новому ортонормированному базису) такая, что матрица Т -1АТ имеет вид (19.1).
Очевидно, любая матрица вида (19.1) – ортогональная.
Лекция 31.