14. Матрица перехода от одного базиса к другому

14.1. Изменение координат вектора при изменении

базиса.

Пусть e={e₁,…,e_n} и e = {e₁,…,e_n} - некоторые базисы в

пространстве L = Lⁿ. Для произвольного вектора x  Lⁿ рас­смотрим разложения x= = и найдем зависи­мость

между координатами х_i и х_i вектора x в этих базисах.

Пусть [ ]=[x], [ ]=[x] и e_j = , j = 1,…,n, t_ij  P - разложение векторов базиса e по базису e. Определим мат­рицу = T=(t_ij)_i,j=1,…,n, столбцами которой являются столцы Т ^j =[ ]. Эта матрица Т называется матрицей перехода от базиса e к базису e. Очевидно, x = = = = 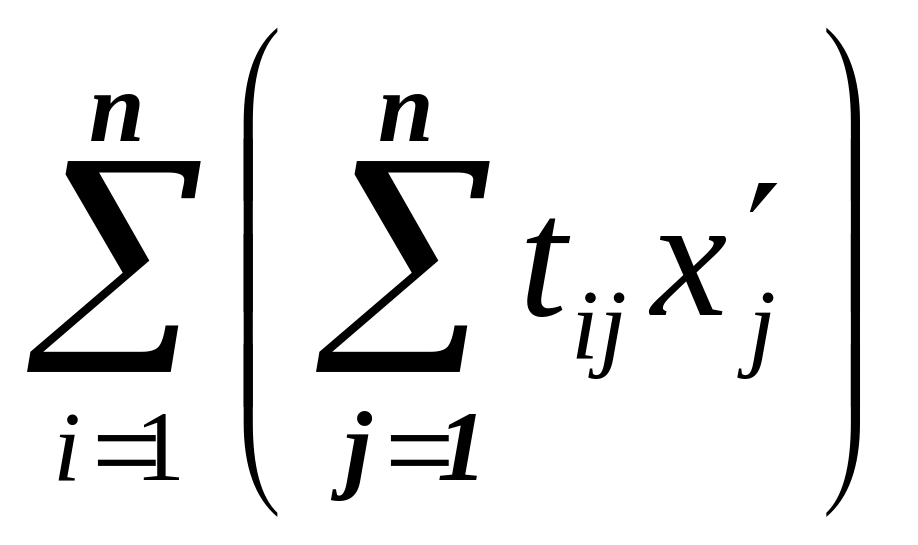е_i  х_i = - это произведение i-ой строки матрицы T= (t_ij ) на столбец [x], и [ ]= [ ] или в сокращенном виде [x] = Т [x].

Следуя (13.1), в матричном виде всё это можно записать так: е = еТ, х = е[x] = е [x] = еТ [x]  [x] = Т [x].

Очевидно, в матрице Т столбцы Т ^j, j=1,…,n, - линейно независимы (как столбцы ко­ординат в базисе е линейно независимых векторов e₁,…,e_n). Поэтому detT  0   T ^-1  [x] = T ^-1[x], то есть T ^-1= .

14.2. Изменение матрицы линейного отображения

при изменении базисов.

Пусть e={e₁,…,e_n} и e = {e₁,…,e_n} – два базиса в про­странстве Lⁿ, u={u₁,…,u_m} и u = {u₁,…,u_m} – два базиса в пространстве L^m, Т₁ = , Т₂ = - матрицы перехода, и  : Lⁿ  L^m - линейное отображение. Найдем зависимость между матрицами [ ] = [] и [ ] = [] линейного отображения  в базисах е, и и е, и соответственно.

Если y =  х, то в базисах е, и имеем [y] = [][x], а в базисах е, и соответственно [y] = [][x]. Но [x] = Т₁ [x],

[y]=Т₂[y], так что Т₂[y]=[]Т₁[x] и [y]=Т₂^-1[]Т₁[x]= [][x]. Отсюда [] = Т₂^-1[]Т₁ или [ ] = ^-1[ ] . В частном случае при Lⁿ = L^m, е = и, е = и для линейного оператора

 : Lⁿ L^п получаем [ ] = [ ] , то есть []= Т^-1[]Т,

где [] = [ ], []= [ ], Т = .

Лемма. Для линейного оператора  : Lⁿ  L^п det[ ] не

зависит от базиса.

Доказательство. det = det[] = det Т^-1det[]det Т=

= det (Т^-1Т)det[] = det Е det[] = det[] = det[ ].

Определение. Определителем det линейного оператора

 : Lⁿ  L^п называется det[ ] - определитель матрицы линейного оператора  в произвольном базисе е .

Из леммы следует, что наше определение корректно.

14.3. Эквивалентные матрицы.

Введем на множестве М_п(Р) квадратных матриц бинар­ное отношение  : будем считать, что для матриц А,В М_п(Р)

выполняется АВ   матрица Т М_п(Р) такая, что |T|  0 и А = Т^-1ВТ.

Утверждение. Отношение  на множестве М_п(Р) явля­ется отношением эквивалентности.

Доказательство.

а)  А М_п(Р) АА, так как при Т= Е имеем А = Е ^–1АЕ, то есть отношение  рефлексивно.

в) Пусть АВ  Т М_п(Р) такая, что А =Т^-1ВТ  В=ТА Т^-1= = (Т^-1)^-1А Т^-1=Т₁^-1 А Т₁, где Т₁ = Т^-1, поэтому В  А, то есть от­ношение  симметрично.

с) Пусть АВ и ВС  Т₁,Т₂ М_п(Р) такие, что А =Т₁^-1ВТ₁ и В =Т₂^-1СТ₂  А= Т₁^-1Т₂^-1СТ₂Т₁= (Т₂Т₁ )^-1С(Т₂Т₁) =Т₃^-1СТ₃, где Т₃ = Т₂Т₁, то есть отношение  транзитивно.

Таким образом, отношение  является отношением экви­валентности.



Далее мы будем использовать следующее

Определение. Матрицы А, В М_п(Р) называются эквивалентными   матрица Т М_п(Р) такая, что |T|  0 и

А = Т^-1ВТ.

Очевидно, множество матриц М_п(Р) разбивается на не­-

пересекающиеся классы эквивалентных матриц. Эти классы образуют фактор-множество М_п(Р). Каждый класс эквива­лентных матриц состоит из матриц некоторого линейного оператора  : Lⁿ  L^п, записанных во всевозможных базисах пространства Lⁿ. Пользуясь этим фактом, можно было дать другое определение отношения  и иначе доказать наше утверждение. Можно было считать, что АВ А и В являются матрицами одного и того же оператора, но записанными в разных (может быть, совпадающих) базисах. Тогда транзитивность отношения  следует из того, что если А и В являются матрицами одного и того же оператора, В и С являются матрицами одного и того же оператора, то, конечно же, А и С являются матрицами одного и того же, того же самого опера­тора. Ещё более очевидна рефлексивность и симметричность отношения .

Основной задачей теории матриц и теории линейных операторов является задача описания фактор-множества М_п(Р), то есть задача выбора в каждом классе единствен­ного наиболее простого представителя, или же выбора наи­более простого вида матрицы линейного оператора в некото­ром «хорошем» базисе - это задача классификации всех матриц (соответственно, всех операторов) с точностью до от­ношения эквивалентности  . Решение этой задачи будет оз­начать, что для любой матрицы мы сможем узнать, какой наиболее простой матрице она эквивалентна, какие пары матриц эквивалентны друг другу, сколько существует раз­личных матриц с точностью до эквивалентности. Для опера­торов это будет означать, что для любого оператора мы смо­жем узнать, к какому наиболее простому виду можно при­вести его матрицу выбором подходящего базиса, сколько существует различных операторов, насколько они похожи, как устроены, каков их геометрический смысл.

Упражнение. Доказать, что если АВ, то detA = detB и rgA = rgB.