3.2. Подстановки.

Пусть Х – конечное множество, Х = {х₁, х₂ ,…, х_n }. Группу подстановок S(X) в этом случае мы будем обозначать S_n. Подстановку  множества Х можно записывать в виде таблицы 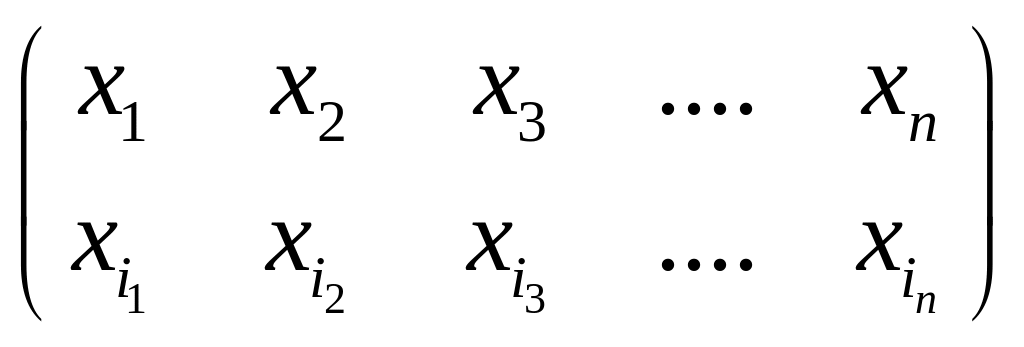 = , где в нижней строке стоят каким-то образом переставленные элементы множества Х. Такая таблица означает, что (х₁)= , (х₂)= , (х₃)= …

Так как  - инъекция, то все элементы нижней строки различные. Так как  - сюръекция, то в нижней строке присутствуют все элементы множества Х. То есть, нижняя строка – это перестановка множества Х. Таким образом, различных подстановок существует ровно столько, сколько имеется различных перестановок множества Х, то есть n!, и, значит, группа S_n подстановок множества из п элементов состоит из n! элементов.

Упражнение. Доказать, что для конечного множества Х

из инъективности  следует её сюръективность, а из сюръективности - инъективность.

Чаще всего мы будем считать, что Х = {1, 2, 3, …, n }. В этом случае подстановки мы будем записывать в виде

 = , где i₁, i₂ ,…, i_n - перестановка чисел 1, 2, 3, …, п.

Для композиции подстановок ₁ ₂ вначале выполняется подстановка ₂, а затем ₁, а для композиции ₁₂ - вначале ₁, а затем ₂ .

Пусть  ^k =  …  - произведение k множителей. Так как Х - конечное множество, то  x Х   S_n { ^kx | k N} – конечное подмножество в Х, то есть  k m такие, что  ^k x =  ^m x. Тогда, если k m, то, очевидно,

 ^k-m x = x. Пусть s – наименьшее натуральное число такое, что  ^sx = x. Тогда подмножество {x,  x,  ²x,  ³x,…, ^s-1x} будем называть циклом, порожденным элементом х, и обозначать O(х). Очевидно, все элементы в O(х) – различны, то есть O(х) состоит из s элементов. Будем считать, что по определению  ⁰ = id, ⁰x= х.

Упражнения.

1. Проверить, что,  ^s+1x = x,  ^s+2x = ²x,  ^-1x =  ^s-1x, …, (О(x))=О(х),  ^k(О(х)) = О(x), О(x) =О(х), О( ^kх) = О(x), О(х) = { ^kx| k =0,1, 2,…, s-1 } = { ^kx| k  Z }.

2. Проверить, что циклы разных элементов либо не пересекаются, либо совпадают.

Таким образом, множество Х разбивается в объединение непересекающихся циклов.

Пусть х = a₁,  x = a₂ ,  ²x = a₃ ,  ³x = a₄ ,…,  ^s-1x = a_s , и соответственно цикл О(х) ={a₁, a₂ ,.., a_s}. Тогда (О(x))= О(х), и  на О(x) является биекцией, которую можно записать в виде таблицы 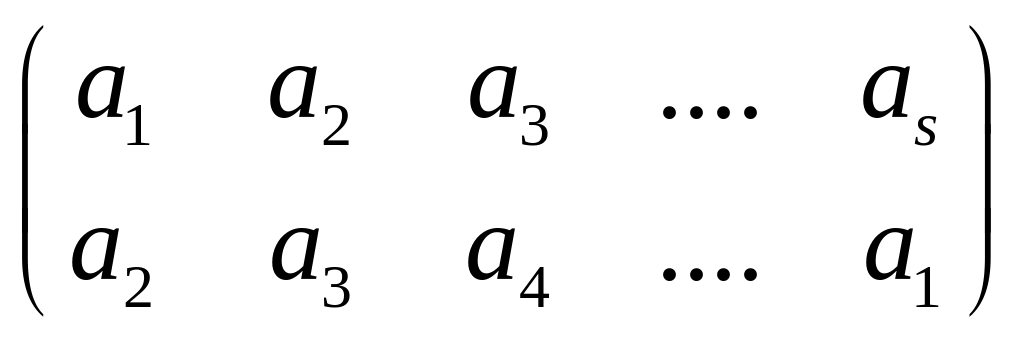или в виде таблицы с одной строкой: (a₁, a₂, a₃,…, a_s ). Запись  в виде такой строки означает, что  a₁= a₂,  a₂= a₃ ,…, a_s-1= a_s ,  a_s= a₁ . Записывая подстановку на каждом цикле в виде одной строки, получим циклическую запись подстановки. Так, например, подстановка

 = в циклической записи имеет вид  =(1, 4, 2, 5)(3)(6, 8, 7).

Определение. Транспозицией будем называть подстановку t_ij такую, что t_ij (i)= j , t_ij (j) = i , t_ij (k) = k при k  i, kj.

Очевидно, t_ij^-1 = t_ij , t_ij² = t_ij .

Утверждение. Любую подстановку   S_n , п  2, можно разложить в композицию транспозиций.

Доказательство по индукции.

1. При п =2 утверждение очевидно, так как S₂ состоит из двух элементов: id и t_ij .

2. Пусть для п – 1 утверждение верно. Рассмотрим   S_n . Пусть (п) = q, и ₁ = t_qn . Тогда ₁ (n) = n, и ₁ – биекция множества {1, 2, 3, …, n -1 } из (п-1)-го элемента. По предположению индукции можно считать, что для ₁ утверждение верно, то есть ₁=₁ ₂ … _r - композиция транспозиций. Но  = t_qn^-1 ₁ = t_qn ₁ = t_qn ₁ ₂ … _r - композиция транспозиций.



Очевидно, разложение подстановки в композицию транспозиций неоднозначно.

На практике очень легко раскладывать подстановку в произведение транспозиций, если она задана в циклической записи. Так, например, легко проверить, что

(1, 3, 7, 2, 4)(5, 6)(8) = t₁₃ t₃₇ t₇₂ t₂₄ t₅₆ .

Будем говорить, что в последовательности чисел i₁, i₂ ,..,i_n два числа i_k и i_l образуют инверсию, если i_k  i_l, но i_k расположено левее i_l . Подстановка  = называется четной, если количество инверсий в её нижней строке

че­тно, и  называется нечетной, если количество инверсий в

её нижней строке нечетно.

Утверждение. Если количество инверсий в нижней строке подстановки  равно m, то  можно разложить в произведение m транспозиций.

Доказательство. Пусть два соседних элемента i_k и i_k+1 в нижней строке подстановки  образуют инверсию. Тогда

₁=  = , и число инверсий в нижней строке у ₁ равно m – 1. Продолжая эту процедуру далее, получим, что существуют транспозиции ₁ ,₂ , …,_m такие, что подстановка _m _m-1 … ₁  не имеет инверсий в нижней строке, то есть _m _m-1 … ₁  = id. Умножая последнее равенство слева на _m , затем на _m-1 и так далее до ₁ , и учитывая, что все _i²= id, получим, что  = ₁ ₂ … _m .



Лекция 4.