2.2. Внутренние усилия

Спроектируем все внутренние силы, действующие в поперечном сечении стержня, на координатные оси и найдем моменты их относительно этих осей.

Крутящий момент – сумма моментов всех внутренних сил, действующих в поперечном сечении стержня, относительно его оси. М_кр > 0, если при взгляде со стороны внешней нормали он совершает вращение по часовой стрелке.

Изгибающие моменты М_у и М_х – сумма моментов всех внутренних сил, действующих в поперечном сечении стержня, относительно его главных центральных осей у и х соответственно. М_у > 0 и М_х > 0, если моменты изгибают стержень так, что его вогнутость располагается со стороны положительной координатной оси х и у соответственно.

Полученные выражения внутренних усилий через внутренние силы называют интегральными зависимостями. Из них нельзя определить внутренние силы, т. е. напряжения σ, τ_zу и τ_zx, так как неизвестен закон их распределения по сечению и значение внутренних усилий.

– называется продольной (осевой) силой.

Что касается внутренних усилий, то их всегда можно определить через внешние силы. В статически определимых конструкциях (системах) для этого достаточно воспользоваться условиями равновесия. Если для определения усилий в сечениях элементов условий равновесия недостаточно, то такие конструкции (системы) называются статически неопределимыми.

Следует отметить, что даже при известных внутренних усилиях определить напряжения из полученных интегральных зависимостей нельзя. Поэтому задача вычисления напряжений всегда является статически неопределимой.

2.3. Выражение внутренних усилий через внешние силы

Рассмотрим равновесие одной из частей стержня, например, левой (обычно рассматривается та часть стержня, на которую действует меньшее количество внешних сил).

На левую часть стержня действуют внешние силы F₁, F₂ и внутренние силы в поперечном сечении 1–1. Так как внутренние усилия являются равнодействующими внутренних сил, то их действие статически эквивалентно действию внутренних сил. Поэтому в сечении 1–1 можно приложить вместо внутренних сил положительные внутренние усилия (рис. 2.3).

Под действием показанных на рисунке сил эта часть стержня находится в равновесии, т. е. для нее должны выполняться шесть уравнений равновесия:

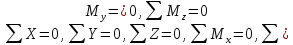
Рис. 2.3. Схема распределения внутренних усилий

в поперечном сечении стержня

Из шести неизвестных усилий только одно проектируется на какую-либо ось или дает момент относительно нее. Поэтому из условий равновесия легко получим:

Из данных формул следует, что:

1) продольная сила N равна алгебраической сумме проекций всех внешних сил, действующих по одну сторону от сечения, на ось стержня. N > 0, если проекция внешней силы направлена от сечения;

2) поперечные силы Q_y и Q_х равны алгебраической сумме проекций всех внешних сил, действующих по одну сторону от сечения, на оси у и х соответственно. Q_у > 0 и Q_х > 0, если при взгляде с положительного направления осей х и у соответственно проекция внешней силы вращает стержень относительно сечения по часовой стрелке;

3) изгибающие моменты равны алгебраической сумме моментов всех внешних сил, действующих по одну сторону от сечения, относительно осей y и х соответственно. 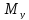> 0 и если внешняя сила или момент так изгибают стержень, что вогнутость его располагается со стороны положительных осей х и y соответственно.

4) крутящий момент М_кр равен алгебраической сумме моментов всех внешних сил, действующих по одну сторону от сечения, относительно оси стержня. М_кр > 0, если при взгляде со стороны внешней нормали к сечению стержня внешняя сила или момент совершают вращение по часовой стрелке. Например, в рассматриваемом случае, от действия силы 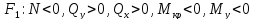и

Таким образом, в общем случае действия внешних сил на стержень в его сечениях возникают четыре вида усилий: продольная сила (N), поперечные силы (Q_y, Q_x), крутящий момент (М_кр) и изгибающие моменты (М_у, М_х).

Каждый вид усилий вызывает характерную для него деформацию. Напряженно-деформированное состояние бруса, вызванное действием:

1) продольной силы (N), называется растяжением или сжатием;

2) поперечной силы (Q) – сдвигом;

3) крутящим моментом (М_кр) – кручением;

4) изгибающим моментом (М_у или М_х) – изгибом.

Все эти виды деформаций называются простыми.

Деформация, вызванная совместным действием двух и более усилий, называется сложной. В таких случаях говорят, что стержень испытывает сложное сопротивление. В расчетной практике наиболее часто встречаются следующие случаи сложного сопротивления.

Поперечный изгиб – деформация, вызванная совместным действием изгибающего момента и поперечной силы.

Пространственный или косой изгиб – деформация, вызванная совместным действием двух изгибающих моментов.

Изгиб с растяжением (сжатием) – деформация, вызванная совместным действием изгибающих моментов и продольной силы.

Изгиб с кручением – деформация, вызванная совместным действием изгибающих и крутящего моментов.