9.4. Дифференциальные зависимости при изгибе. Контроль правильности построения эпюр

Балка, изображенная на рис. 9.10, а, нагружена произвольной распределенной нагрузкой q = f (z).

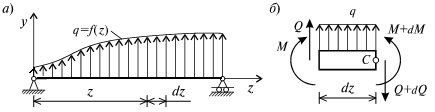
Рис. 9.10. Однопролетная балка, загруженная произвольной

распределенной нагрузкой

Выделим из балки элемент длиной dz и приложим по его краям положительные внутренние усилия (рис. 9.10, б). Считаем, что в пределах малого участка dz нагрузка q распределена равномерно. Составим уравнения равновесия проекций всех сил на вертикальную ось y и суммы моментов всех сил относительно поперечной оси x, проходящей через точку С (рис. 9.10, б), получим:

Q_y + q dz  Q_y  d Q_y = 0;

M_x + Q_y dz + q dz dz/2  M_x  d M_x = 0.

В данных уравнениях выполним упрощения и отбросим величины второго порядка малости, получим:

; ,

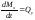откуда

.

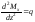Проверки правильности построения эпюр внутренних силовых факторов при поперечном изгибе.

1. Эпюра M_x на участках балки между сосредоточенными силами, между сосредоточенной силой и моментом, между нача­лом или концом действия равномерно распределенной нагрузки и сосредоточенной силой или моментом всегда изменяется по линейному закону (прямая под углом к нулевой линии). Если эпюра М строится на растянутых волокнах, то в пределах действия равномерно распределенной нагрузки она изменяется по закону квадратной пара­болы с выпуклостью в сторону действия нагрузки.

2. Под точкой приложения сосредоточенной силы эпюра M_x имеет перегиб с направлением в сторону действия силы.

3. На эпюре M_x в сечении, где действует сосредоточенный момент m, будет скачок, равный его величине.

4. Над шарнирными опорами однопролетной балки изгибающий момент может быть только в тех случаях, когда в опорных сечениях приложены сосредоточенные моменты или когда на консолях, расположенных за опорами, приложены нагрузки. Во всех других случаях изгибающие моменты в шарнирных опорах равны нулю.

5. В сечениях, где поперечная сила Q_y принимает нулевое значение и меняет знак, изгибающий момент M_x достигает экстремальных значений.

6. Поперечная сила Q_y на участке равна нулю, если во всех сечениях по длине этого участка M_x = const.

7. Эпюра Q_y постоянна на участках балки между сосредоточенными нагрузками и изменяется по линейному закону лишь на участках, где действует равномерно распределенная нагрузка.

8. Эпюра Q_y в точках приложения сосредоточенных вертикальных сил (F, R_A, R_B) имеет скачки, равные по величине приложенным в этих сечениях сосредоточенным силам, причем их направление всегда совпадает с направлением этих сил.

9.5. Касательные напряжения при изгибе. Эпюры напряжений

При поперечном изгибе в сечениях балки кроме изгибающего момента М возникает и поперечная сила Q. Поэтому кроме нормальных напряжений в сечениях балки возникают и касательные напряжения. Определим касательные напряжения, возникающие в балке прямоугольного поперечного сечения.

Возьмем два произвольных сечения по длине балки I–I и II–II, расположенных на расстоянии dz друг от друга (рис. 9.11, а). Согласно эпюрам, в сечении I–I действуют поперечная сила Q_x и изгибающий момент М_х, а в сечении II–II – поперечная сила Q_х и изгибающий момент М_x + dM_x.

Рис. 9.11. Схема балки к расчету касательных напряжений

Нормальные напряжения, вызванные изгибающими моментами в сечениях I–I и II–II, соответственно определяются по формулам:

; .

Проведем горизонтальное сечение тп на расстоянии у от нейтральной оси балки и рассмотрим равновесие выделенного элемента (рис. 9.11, б).

Равнодействующие нормальных напряжений, которые действуют на левую и правую боковые грани параллелепипеда, обозначим N₁ и N₂. Площадь граней обозначим А_отс (часть отсеченной площади поперечного сечения, расположенная между горизонтальным сечением mn и нижним основанием сечения балки).

,

где 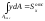, тогда ;

.

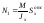Выделенный элемент (рис. 9.12) находится в равновесии и для него справедливо условие равновесия Σх = 0.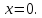

Предположим, что в горизонтальном сечении параллелепипеда действуют касательные напряжения τ, которые равномерно распределены по ширине сечения.

Площадь горизонтального сечения равна bdz.

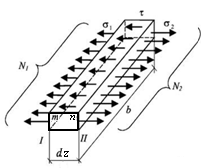
Рис. 9.12. Схема распределения внутренних сил

Из уравнения равновесия получим:

Σх = N₂ – N₁ – τbdz = 0,

откуда

.

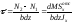Используя зависимость

,

окончательно получим (формула Д. И. Журавского):

,

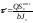где Q – величина поперечной силы в сечении;

S_x^отс – статический момент отсеченной части площади поперечного сечения, расположенной между рассматриваемым волокном и краем сечения балки относительно нейтральной оси;

b – ширина сечения в той точке, где определяются касательные на-пряжения;

J_x – осевой момент площади поперечного сечения относительно нейтральной оси.

Согласно закону парности касательных напряжений они возникают и в поперечных сечениях балки.

Знак касательных напряжений определяется знаком поперечной силы Q.

Рассмотрим, как распределяются касательные напряжения в балках различного поперечного сечения.

1. Прямоугольное сечение.

Для данного сечения

и меняется только величина статического момента S_x^отс. Возьмем произвольную точку С, отстоящую от центральной оси сечения на расстоянии у (рис. 9.13, а). Проведем через эту точку сечение параллельно оси х. Площадь отсеченной части сечения:

.

Рис. 9.13. Эпюра касательных напряжений

для прямоугольного сечения

Статический момент этой площади:

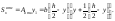
Подставим в формулу Журавского найденное значение S_x^отс.

С учетом того что

,

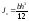получим .

Так как у входит в формулу во второй степени, следовательно, эпюра τ будет параболической. В наиболее удаленных от нейтральной оси точках при у = ± h/2 τ = 0.

В нейтральном слое при у = 0 касательные напряжения будут иметь максимальное значение, т. е.

.

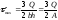Эпюра касательных напряжений для прямоугольного сечения изображена на рис. 9.13, б.

2. Круглое сечение.

Для круглого сечения (рис. 9.14) формула Журавского для вертикальной составляющей касательного напряжения может быть записана в следующем виде:

.

Рис. 9.14. Эпюра касательных напряжений

для круглого сечения

Согласно полученной формуле, эпюра τ будет параболической. В наиболее удаленных от нейтральной оси точках при у = R τ = 0. Наибольшие касательные напряжения будут в нейтральном слое при у = 0. Эпюра касательных напряжений представлена на рис. 9.14, б.

3. Двутавровое сечение.

При построении эпюры касательных напряжений для двутаврового сечения необходимо учитывать, что изменяются не только статический момент площади, но и ширина сечения. Поэтому эпюра касательных напряжений строится по характерным точкам (рис. 9.15).

В точке 1, S_x^отс = 0, поэтому τ = 0. В месте примыкания полки к стенке (точки 2 и 2^') будем считать, что эти точки расположены бесконечно близко одна от другой, причем точка 2 принадлежит полке, а точка 2^' – стенке.

В точке 2 ширина сечения равна b, а статический момент определяется как статический момент полки с размерами b × t. Для точки 2^' статический момент такой же, как для точки 2, но ширина сечения равна d (рис. 9.15, а), и касательные напряжения резко возрастают. Наибольшие касательные напряжения возникают на нейтральной оси и определяются по формуле

.

Рис. 9.15. Эпюра касательных напряжений

для двутаврового сечения

Касательные напряжения в остальных точках определяются из условия симметрии сечения. Эпюра распределения касательных напряжений изображена на рис. 9.15, б.

На рис. 9.16 показан вид эпюр для некоторых других сечений.

Рис. 9.16. Эпюры касательных напряжений для различных сечений

Анализируя эпюры касательных напряжений, можно сделать следующие выводы.

1. Вид эпюры τ зависит от формы поперечного сечения.

2. Касательные напряжения по сечению распределяются неравномерно и обычно достигают максимального значения на нейтральной оси сечения.