13.2. Элементарная теория удара. Динамический коэффициент. Продольный и поперечный удар

Под ударом понимается взаимодействие движущихся навстречу друг другу тел в результате их соприкосновения, связанное с резким изменением скоростей точек этих тел за весьма малый промежуток времени.

Ударная нагрузка является динамической. Время удара измеряется в тысячных, а иногда и миллионных долях секунды, а сила удара достигает большой величины, например, действие кузнечного молота на кусок металла, удар падающего груза при забивке свай и др.

За очень малый промежуток времени скорость ударяющегося тела становится равной нулю. В этот момент напряжения и деформации в системе достигают наибольших значений. Целью расчета на удар и является определение наибольших деформаций и напряжений.

Система, подвергающаяся удару, может испытывать различные деформации, такие как сжатие, растяжение, изгиб, кручение, изгиб с кручением и др. Поэтому различают продольный, поперечный и скручивающий удары (рис. 13.5).

Рис. 13.5. Схемы ударных нагрузок

На рис. 13.5, а и 13.5, б показаны продольные удары – сжимающий и растягивающий, на рис 13.5, в показан поперечный изгибающий удар.

Скручивающий удар имеет место при падении груза G с высоты h или при резком снижении угловой скорости вала с маховиком, например, при внезапной его остановке (рис. 13.5, г, д).

Точное решение задачи о напряжениях и деформациях при ударе затруднительно, потому что неизвестен закон изменения скорости при соударении тел и, следовательно, действующих при ударе нагрузок, неизвестны силы сопротивления при ударе, чрезвычайно сложен закон распространения скорости деформации в системе, воспринимающей удар.

В практике применяют упрощенные методы расчета, основанные на следующих основных допущениях:

1) деформации стержня от ударяющего груза распространяются по всей длине стержня, они подчиняются закону Гука и подобны деформациям, возникающим от статического приложения того же груза. Поэтому связь между динамическими силами и перемещениями остается такой же, как и при статической нагрузке;

2) опорные устройства, как правило, полагают абсолютно жесткими;

3) ударяющее тело является абсолютно жестким и при ударе не отскакивает от системы.

Изучение напряжений и деформаций при ударе основано на использовании закона сохранения энергии. При этом предполагается, что кинетическая энергия падающего груза А численно равна потенциальной энергии деформации упругой системы U:

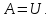
Рассмотрим сначала расчет на удар в случаях, когда масса упругого тела, подвергающегося удару, мала и ею можно пренебречь. Продольный удар груза G падает с высоты h и ударяется о стержень, вызывая его сжатие на величину , которая больше деформации стержня ∆_ст при статическом действии груза G (рис. 13.6).

Кинетическая энергия падающего груза равна:

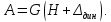
Потенциальная энергия численно равна площади треугольника диаграммы F _дин– ∆_дин (рис. 13.7).

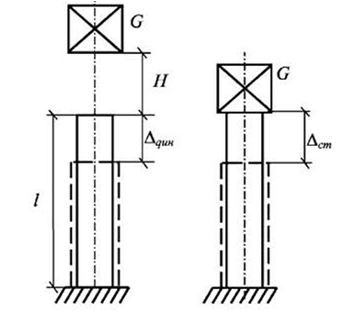
Рис.13.6. Схема удара сжатием

Рис. 13.7. Схема для определения потенциальной

энергии деформации при ударе

С учетом зависимости А = U имеем:

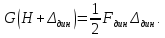
Выразим нагрузки через деформации:

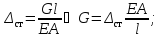
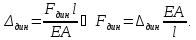
Далее имеем:

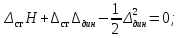
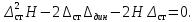
Получим квадратное уравнение для определения

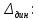
В формуле перед корнем следует взять знак «плюс», так как , тогда получим:

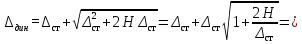
Динамический коэффициент будет равен:

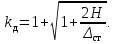
Зная коэффициент, можно определить и напряжения:

Динамический коэффициент зависит от величины:

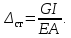
Следовательно, напряжения при ударе зависят не только от площади поперечного сечения стержня A (как при статическом приложении нагрузки), но и от длины стержня и жесткости материала Е. Чем больше длина l, тем напряжения при ударе будут меньшими. С увеличением модуля упругости напряжения увеличиваются.

С целью уменьшения динамических напряжений в технике используются различные амортизаторы, увеличивающие податливость стержня (резиновые прокладки, пружины) (рис. 13.8).

Рис. 13.8.  Схема удара сжатием

с амортизатором – пружиной

В этом случае

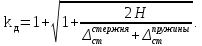
Рассмотрим частные случаи.

1. При мгновенном приложении нагрузки, когда H = 0:

При этом напряжение и перемещение в два раза больше, чем при статическом приложении нагрузки.

2. Если высота падения груза Н велика, т. е.

то единицей в подкоренном выражении для определения динамического коэффициента можно пренебречь, тогда:

3. При очень больших величинах

можно пренебречь единицей и перед корнем. Тогда

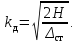
Если известна скорость падения груза, а не высота падения, то динамический коэффициент может быть выражен через скорость. При свободном падении

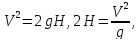
тогда

·

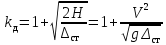Определение динамического коэффициента при продольном ударе стержней с переменным поперечным сечением.

Сравним прочность двух стержней, подвергающихся продольному удару. Один стержень имеет постоянную площадь сечения А, а другой на участке длиной l имеет площадь сечения A, а в пределах остальной длины стержня – nА, где п > 1 (рис. 13.9).

При статическом воздействии груза F оба бруса равнопрочны, так как наибольшие напряжения (при расчете без учета концентрации напряжений) в каждом из них

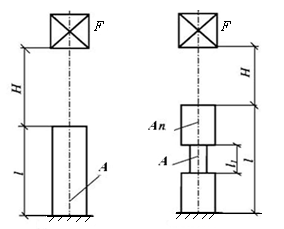
Рис. 13.9. Схема продольного удара

При ударном действии нагрузки динамический коэффициент для первого бруса равен:

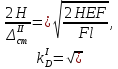
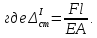
Для второго бруса

Если длина l₁ очень мала, что имеет место, например, при наличии поперечных выточек, то приближенно можно принять:

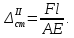
Динамический коэффициент для второго стержня:

т. е. в раз больше, чем для первого стержня. Таким образом, второй брус при ударном действии нагрузки менее прочен, чем первый. Поэтому оказывается более выгодным уменьшать площадь сечения по всей длине стержня.

В качестве примера можно привести болт, передающий от одной части конструкции на другую растягивающий удар. Участок болта с нарезкой, имеющий меньший диаметр, будет работать как выточка. Обрыв болта весьма вероятен. Для улучшения конструкции необходимо сделать его площадь всюду (или почти всюду) равной площади по внутреннему диаметру нарезки. Этого можно достигать путем обтачиванием болта или высверливанием в нем канала (рис. 13.10).

Рис. 13.10. Болт, работающий на растягивающий удар

Поперечный изгибающий удар.

Рассмотрим балку, свободно лежащую на двух шарнирных опорах. Балка изгибается под действием груза F, падающего с высоты H (рис. 13.11).

Рис. 13.11. Схема поперечного изгибающего удара

Динамический коэффициент в этом случае определяется по формуле

где f_ст – прогиб балки в месте падения груза при статическом ее нагружении.

Если а = b = l/2, то

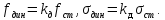
Так же, как и при продольном ударе, внезапное приложение нагрузки на балку вызывает напряжение

Условие прочности при изгибающем ударе имеет такой же вид, как и при продольном, т. е.

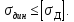
Учет массы тела, испытывающего удар.

Если груз падает на стержень, обладающий значительной массой, то решение значительно усложняется. Можно применить приближенное решение, оно сводится к замене реальной массы стержня приведенной массой, сосредоточенной в месте удара. Учет массы тела может оказать существенное влияние на динамические напряжения.

Если груз G падает на стержень, вес которого Q значителен, то динамический коэффициент определяется по формуле

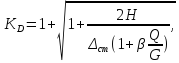
где Н – высота падения;

β – коэффициент приведения массы стержня. Он зависит от способов закрепления концов стержня и вида удара (продольный, поперечный и т. д.). Для определения коэффициента β рассматривают кинетическую энергию стержня при его движении вследствие удара;

Q – вес ударяемого стержня;

G – вес падающего груза.

Рассмотрим частные случаи.

1. Продольный удар. Стержень постоянного сечения A защемлен одним концом. Объемный вес материала γ. Будем считать, что в момент удара верхний конец ударяемого стержня получает скорость V. Скорость нижележащих сечений стержня изменяется по линейному закону, достигая нулевого значения в нижнем сечении стержня (рис. 13.12).

Скорость движения произвольного сечения, расположенного на расстоянии х от нижнего сечения, будет равна:

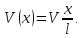
Рис. 13.12. Схема продольного удара

Так как частицы стержня движутся, то стержень обладает кинетической энергией. Кинетическая энергия элементарной частицы стержня длиной dx будет равна:

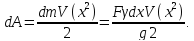
Кинетическая энергия всего стержня с учетом данной формулы равна:

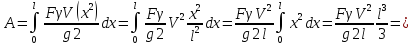
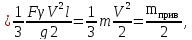
где т_прив – приведенная масса стержня.

2. Поперечный удар. В этом случае балка постоянного поперечного сечения защемлена одним концом и испытывает удар груза на свободном конце (рис. 13.13)

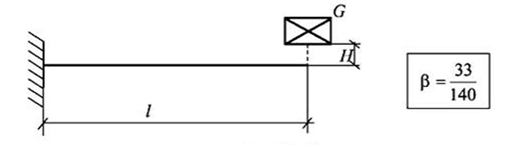
Рис. 13.13. Схема консольной балки при ударе

Для балки, закрепленной шарнирно, удар приходится посередине пролета (рис. 13.14).

Рис. 13.14. Схема поперечного удара для однопролетной балки

Учет массы ударяемого стержня может значительно уменьшить динамический коэффициент.