МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА
И ПРОДОВОЛЬСТВИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
ГЛАВНОЕ УПРАВЛЕНИЕ ОБРАЗОВАНИЯ, НАУКИ И КАДРОВ
Учреждение образования
«БЕЛОРУССКАЯ ГОСУДАРСТВЕННАЯ
СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ»
Е. В. Афанасенко, М. В. Нестеров
Механика материалов
Рекомендовано учебно-методическим объединением
по образованию в области сельского хозяйства в качестве
пособия для студентов учреждений высшего образования
специальности 1-74 05 01 Мелиорация и водное хозяйство
Горки
БГСХА
2012
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА
И ПРОДОВОЛЬСТВИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
ГЛАВНОЕ УПРАВЛЕНИЕ ОБРАЗОВАНИЯ, НАУКИ И КАДРОВ
Учреждение образования
«БЕЛОРУССКАЯ ГОСУДАРСТВЕННАЯ
СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ»
Е. В. Афанасенко, М. В. Нестеров
Механика материалов
Рекомендовано учебно-методическим объединением
по образованию в области сельского хозяйства в качестве
пособия для студентов учреждений высшего образования
специальности 1-74 05 01 Мелиорация и водное хозяйство
Горки
БГСХА
2012
УДК 539.3/.6(075.8)
ББК 30.121я7
А94
Рекомендовано Научно-методическим советом БГСХА
20.06.2012 Г. (протокол № 10)
и методической комиссией
мелиоративно-строительного факультета
11.06.2012 Г. (протокол № 10)
Авторы:
кандидат технических наук, доцент Е. В. Афанасенко;
кандидат технических наук, доцент М. В. Нестеров
Рецензенты:
кандидат технических наук, научный сотрудник
РНДУП «Институт мелиорации» НАН Беларуси А. С. Анженков;
кандидат технических наук, доцент, заведующий кафедрой сопротивления металлов и теории упругости
УО «БНТУ» С. И. Зинкевич
|
А94 |
Афанасенко, Е. В. Механика материалов : пособие / Е. В. Афанасенко, М. В. Нестеров. – Горки : БГСХА, 2012. – 342 с. ISBN 978-985467-410-0.
Рассмотрены теоретические вопросы по основным разделам курса «Механика материалов», приведены примеры расчетов деталей машин, элементов конструкций и сооружений на прочность, жесткость и устойчивость. Для студентов учреждений высшего образования специальности 1-74 05 01 Мелиорация и водное хозяйство. |
УДК 539.3/.6(075.8)
ББК 30.121я7
ISBN 978-985467-410-0 © УО «Белорусская государственная
сельскохозяйственная академия», 2012
Введение
Механика материалов наука о прочности, жесткости и устойчивости элементов машин и сооружений. Методами механики материалов выполняются расчеты, позволяющие определять надежные и наиболее рациональные размеры поперечных сечений элементов инженерных конструкций, а также их целесообразную форму.
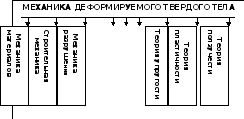
Механика материалов рассматривается как раздел механики деформируемых твердых тел.
В отличие от теоретической механики механика материалов рассматривает задачи, в которых наиболее существенными являются свойства твердых деформируемых тел, законами движения тела как жесткого целого пренебрегают.
Методы механики материалов базируются на упрощенных гипотезах, которые позволяют решать разнообразные инженерные задачи и получать достаточно точные результаты расчетов.
1. Основные определения, методы и принципы механики материалов
1.1. Задачи, цель и предмет механики материалов
Главной задачей курса является формирование знаний и навыков у студентов для применения математического аппарата при решении прикладных задач механики материалов, анализа полученных численных результатов и выбора наиболее оптимальных конструктивных решений.
Цели дисциплины: теоретическая и практическая подготовка для проведения расчетов на прочность, жесткость и устойчивость; развитие инженерного мышления студентов.
В процессе производственной деятельности человек создает и использует множество разнообразных конструкций. К их числу относятся различные машины и механизмы, приборы, строительные сооружения, транспортные средства и т. п. В процессе эксплуатации на конструкции действуют внешние силы и нагрузки и при этом должна быть обеспечена надежность конструкций. Любая конструкция или ее элементы считаются надежными, если обеспечена их прочность, жесткость и устойчивость.
Прочностью называется способность конструкции и ее элементов выдерживать определенную нагрузку не разрушаясь. Под жесткостью понимается способность конструкции и ее элементов при действии нагрузок заданной величины изменять свою форму и размеры в допускаемых пределах, не нарушающих ее нормальную работу. Устойчивость – это способность конструкции сохранять первоначальную форму упругого равновесия. Упругая конструкция находится в устойчивом состоянии, если, будучи выведенной из этого состояния какими-либо воздействиями, возвращается в него после устранения этих воздействий.
Изменение первоначальной формы упругого равновесия называется потерей устойчивости.
Механика материалов – наука, разрабатывающая инженерные методы расчета на прочность, жесткость и устойчивость, на основании которых устанавливаются рациональные формы и размеры элементов машин и сооружений, обеспечивающие их надежность и экономичность.
Следует заметить, что принципы и методы этих расчетов разрабатываются также в ряде других наук, таких как механика твердого деформируемого тела, теория упругости, строительная механика, теория пластичности, теория ползучести, механика разрушения и др.
Механика материалов – наука экспериментально-теоретическая, которая отличается от других наук тем, что использует упрощающие гипотезы и простой математический аппарат в расчетах. Решения задач, полученных методами механики материалов, как правило, выражаются в виде простых формул, удобных для практического использования.
Результаты, полученные в механике материалов, широко используются во всех областях техники, где существенными являются надежность и экономичность конструкций. Вместе с тем следует иметь в виду, что эти результаты являются приближенными и имеют ограниченную область применения. Более точные решения, имеющие более широкую область применения, могут быть найдены методами механики твердого деформируемого тела.
Необоснованный расчетами выбор размеров конструкции приводит к увеличению ее веса, нерациональному использованию материалов и повышению стоимости конструкции или резко снижает ее надежность.