9.13. Пример расчета

Задача 1. Для балки, изображенной на рис. 9.35, а, построить эпю-ры поперечных сил и изгибающих моментов.

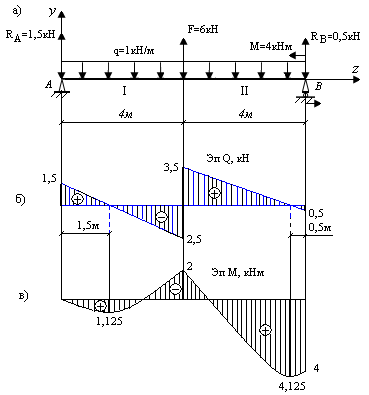
Рис. 9.35. Схема построения эпюр Q и M

для однопролетной балки

Решение.

1. Определим опорные реакции:

;

.

2. Выполним проверку:

,

реакции определены верно.

3. Разбиваем балку на участки (рис. 9.35, а).

4. Составим общие уравнения Q и М для каждого участка балки. Обходим балку слева направо:

1-й участок: 0 ≤ z₁ ≤ 4 м;

;

.

Определим экстремальное значение момента на 1-м участке:

Q₁ = R_A – qz₁ = 1,5 – 1z₁ = 0, z₁ = 1,5 м;

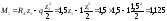кНм.

Обходим балку справа налево:

2-й участок: 0 ≤ z₂ ≤ 4 м;

;

.

Определим экстремальное значение момента на 2-м участке:

Q₂ = –R_В + qz₂ = –0,5 + 1z₂ = 0, z₂ = 0,5 м;

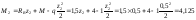кНм.

5. По полученным значениям ординат строим окончательные эпюры Q и M (рис. 9.35, б, в).

Задача 2. Для балки, изображенной на рис. 9.36, а, построить эпюры поперечных сил и изгибающих моментов.

Решение.

1. Определим опорные реакции:

;

.

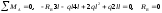2. Выполним проверку:

,

реакции определены верно.

3. Разбиваем балку на участки (рис. 9.36, а ).

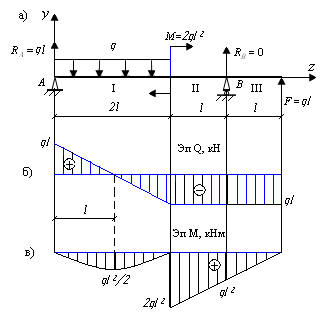
Рис. 9.36. Схема построения эпюр Q и M

для однопролетной балки

4. Составим общие уравнения Q и M для каждого участка балки. Обходим балку слева направо:

1-й участок: 0 ≤ z₁ ≤ 2l;

;

.

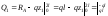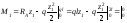Определим экстремальное значение момента на 1-м участке:

Q₁ = R_A – qz₁ = ql – qz₁ = 0, z₁ = l м;

.

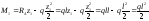2-й участок: 0 ≤ z₂ ≤ l;

;

.

Обходим балку справа налево:

3-й участок: 0 ≤ z₃ ≤ l;

Q₁ = –F = –const;

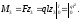
5. По полученным значениям ординат строим окончательные эпюры Q и M (рис. 9.36, б, в).

Задача 3. Для балки, изображенной на рис. 9.37, а, построить эпюры поперечных сил и изгибающих моментов.

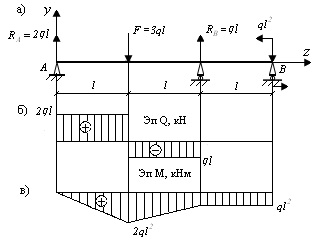
Рис. 9.37. Схема построения эпюр Q и M

для однопролетной балки

Решение.

По аналогии с решениями предыдущих задач определяем орди-наты эпюр Q и M. Окончательные эпюры Q и M изображены на рис. 9.37, б, в.

Задача 4. Проверить прочность балки таврового сечения при [σ]_р = 30 МПа и [σ]_сж = 60 МПа (рис. 9.38, а).

Решение.

1. Определим координаты центра тяжести таврового сечения относительно оси, проходящей по нижнему основанию сечения (рис. 9.38, б):

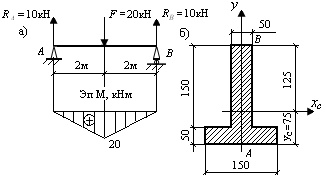
Рис. 9.38. Схема однопролетной балки для расчета на прочность

2. Определим осевой момент инерции таврового сечения относительно оси x_c:

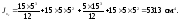
3. Определим моменты сопротивления таврового сечения в сечениях, наиболее удаленных от оси x_c:

- растянутая зона

;

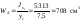- сжатая зона

.

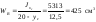4. Определим максимальный изгибающий момент в поперечных сечениях балки:

.

5. Определим нормальные напряжения в сечениях А и B:

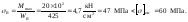
Условие прочности соблюдается.

Задача 5. Для заданной схемы нагружения балки (рис. 9.39, а) подобрать прямоугольное сечение, [σ] = 200 МПа.

Рис. 9.39. Схема однопролетной балки для определения

размеров сечения

Решение.

1. Определим опорные реакции:

, R_A = 40 кН;

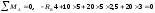, R_В = 90 кН.

2. Строим эпюру изгибающих моментов, которая изображена на рис. 9.39, б. По эпюре определяем значение M_max = 40 кНм.

3. Из условия прочности находим момент сопротивления прямоугольного сечения:

,

откуда ,

далее ;

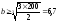см,

окончательно b = 6,7 см, h = 2b = 13,4 см.

Задача 6. Для балки, изображенной на рис. 9.40, а, подобрать сечение, состоящее из двух швеллеров, [σ] = 160 МПа.

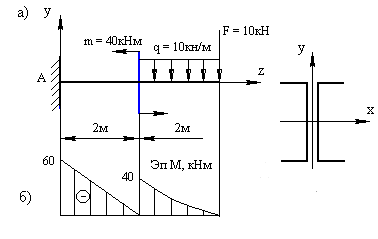
Рис. 9.40. Схема консольной балки

для подбора поперечного сечения

Решение.

1. Строим эпюру изгибающих моментов, двигаясь по балке от конца консоли к заделке (рис. 9.40, б). М_max = 60 кНм.

2. Из условия прочности определим момент сопротивления составного сечения балки:

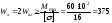см³,

откуда W_ш = 188 см³.

По ГОСТ 8240–72 подбираем швеллер № 22 с моментом сопротивления W_х = 192 см³.

Задача 7. Двутавровая балка № 36 загружена, как указано на рис. 9.41, а. Определить допускаемую грузоподъемность балки, если [σ] = 160 МПа.

Рис. 9.41. Схема двутавровой балки для расчета

допускаемой грузоподъемности

Решение.

1. По ГОСТ 8239–72 для двутавра № 36 W_х = 743 см³.

2. Из условия прочности

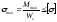
определим

,

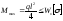тогда 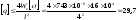кН/м,

[F] = [q]l = 29,7  4 = 118,9 кН.

Задача 8. Интегрированием дифференциального уравнения изогнутой оси балки, изображенной на рис. 9.42, определить прогиб и угол поворота конца консоли.

Рис. 9.42. Схема консольной балки для определения

перемещений

Решение.

1. Определим опорные реакции в заделке:

;

.

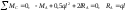2. Разобьем балку на участки (рис. 9.42) и составим уравнения упругой линии для каждого из них:

1-й участок:

,

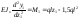проинтегрируем дважды это уравнение, получим:

;

.

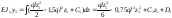2-й участок:

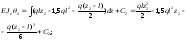
Рассмотрим начальные условия:

при z₁ = l = z₂; θ₁ = θ₂; С₁ = С₂ = С;

при z₁ = l = z₂; у₁ = у₂; D₁ = D₂ = D;

при z₁ = 0; θ₁ = 0; С = 0;

при z₁ = 0; у₁ = 0; D = 0.

Тогда последние два уравнения принимают вид:

;

,

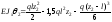тогда при z₂ = 2l; ;

.
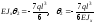
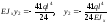