9.8. Главные напряжения при изгибе

Для исследования напряженного состояния в произвольной точке балки, испытывающей поперечный изгиб, выделим вокруг исследуемой точки элементарную призму. Пусть вертикальная площадка призмы является частью поперечного сечения балки, а ее наклонная площадка составляет произвольный угол  с осью z. Принимаем, что выделенный элемент имеет следующие размеры по координатным осям: dz по оси z; dy по оси у; по оси x  размер, равный ширине балки (рис. 9. 21).

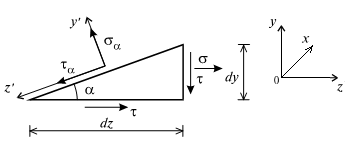
Рис. 9.21. Схема элементарной призмы

Так как вертикальная площадка выделенного элемента принадлежит поперечному сечению балки, испытывающему поперечный изгиб, то нормальные напряжения  на этой площадке определяются по формуле 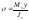, а касательные напряжения τ – по формуле Журавского. Касательные напряжения на горизонтальной площадке призмы с учетом закона парности касательных напряжений также равны τ. С учетом принятых допущений при изгибе (продольные волокна балки не деформируют друг друга), нормальные напряжения на этой площадке равны нулю.

Обозначим величины нормальных и касательных напряжений на наклонной площадке через σ_а и τ_а соответственно. Пусть площадь наклонной площадки равна dА. Тогда площади вертикальной и горизонтальной площадок будут равны dА sin α и dА cos α соответственно.

Составляя уравнения равновесия для элементарной вырезанной призмы (рис. 9.21), получим:

Σу′ = 0; Σz′ = 0,

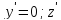откуда будем иметь:

σ_adA – τ cos α dA sin α – τ sin α dA cos – σ sin α dA sin α = 0;

τ_adA – τ sin α dA sin α – τ cos α dA cos α – σ cos α dA sin α = 0.

После несложных преобразований получим окончательные выражения напряжений на на­клонной площадке:

σ_a = σ sin² α + τ sin 2α;

.

Определим значение  = ₀, при котором напряжение _ принимает экстремальное значение. Возьмем производную функции _ по  и приравняем ее нулю:

.

Пусть  = ₀, тогда

.

Окончательно будем иметь:

.

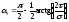Согласно последнему выражению, экстремальные напряжения возникают на двух взаимно перпендикулярных площадках, называемых главными, а сами напряжения на этих площадках называются главными напряжениями.

Сопоставим формулы τ_а и , получим

,

откуда следует, что касательные напряжения на главных площадках всегда равны нулю.

С учетом известных тригонометрических тождеств

;

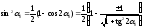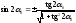
и формулы определим главные напряжения:

.

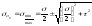9.9. Деформации при изгибе. Угол поворота и прогиб сечения. Дифференциальное уравнение изогнутой оси балки

При поперечном изгибе ось балки принимает вид кривой, расположенной в плоскости действия внешних нагрузок. При этом точки оси получают поперечные перемещения у, а поперечные сечения совершают повороты относительно своих нейтральных осей на угол θ, равный углам наклона касательной и изогнутой оси балки (рис. 9.22).

Прогибы и углы поворотов поперечных сечений в балках являются функциями координаты z. Их определение необходимо для расчета балки на жесткость.

Рассмотрим изгиб балки в одной из главных плоскостей, например, в плоскости yz. Как показывает практика, элементы сооружений испытывают незначительные деформации (y_max/l = 10^2…10^3, где y_max  максимальный прогиб; l  пролет балки).

Рис. 9.22. Схема кривой оси балки при поперечном изгибе

В данном случае неизвестными функциями, определяющими положение точек поперечных сечений балки, являются y (z) и θ (z) =  (z). Из геометрических построений (рис. 9.22) видно, что угол наклона касательной к оси z и угол поворота поперечного сечения при произвольном значении z равны между собой. В силу малости углов поворота сечений имеем:

θ (z) ≈ tg θ (z) = y′ (z).

Из курса высшей математики известно, что кривизна плоской кривой y (z) выражается формулой

.

Если в последнем выражении отбросить величину второго порядка малости, то с учетом формулы

после несложных математических преобразований получим дифференциальное уравнение изогнутой оси балки:

,

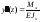где J_x – момент инерции поперечного сечения балки относительно ее

нейтральной оси;

Е  модуль упругости материала;

EJ_x   жесткость балки.

Данное уравнение в общем случае справедливо для чистого изгиба балки, т. е. когда изгибающий момент M_x имеет постоянное значение, а поперечная сила Q_y равна нулю. Это уравнение используется и в случае поперечного изгиба, при котором искривлениями поперечных сечений за счет их сдвигов пренебрегаем (гипотеза плоских сечений).

Введем еще одно упрощение, связанное с углом поворота поперечного сечения. Если изогнутая ось балки является пологой кривой, то углы поворота сечений можно принимать равными первой производной от прогибов. Отсюда следует, что прогиб балки принимает экстремальные значе­ния в тех сечениях, где угол поворота равен нулю.

В общем случае для того чтобы найти функции прогибов y (z) и углов поворота   (z), необходимо решить последнее уравнение с учетом граничных условий между смежными участками.

Для балки, имеющей несколько участков, определение формы упругой линии является достаточно сложной задачей, так как уравнение изогнутой оси балки, записанное для каждого участка, после интегрирования содержит две произвольные постоянные.

На границах соседних участков прогибы и углы поворота сечений являются непрерывными функциями. Это позволяет определить необходимое число граничных условий для вычисления произвольных постоянных интегрирования.