7.6. Круг напряжений Мора

Зависимость напряжений от угла наклона площадки, на которой они действуют, имеет простую геометрическую интерпретацию в виде диаграммы, которая называется кругом напряжений Мора. Обозначим:

Тогда напряжения на наклонных площадках можно представить в виде:

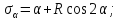
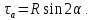
Эти уравнения представляют окружность в параметрической форме. Они эквивалентны уравнению:

Используя круги Мора, можно решать два типа задач.

Первый тип. Пусть известны напряж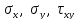ения на произволь-ных площадках. Требуется найти главные напряжения 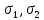и положение главных площадок.

Решение. По оси (рис. 7.6) отложим отрезок , равный по величине

Рис. 7.6. Схема круга Мора для нахождения главных напряжений

и положения главных площадок

Из точки в направлении оси отложим отрезок соответствующий . Аналогично построим точки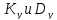, равные напряжениям. Соединив точки , получим точку С пересечения отрезка с осью . Вокруг точки С опишем окружность диаметром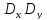. Это и будет окружность напряжений Мора.

Точки А и В пересечения окружности с осью σ соответствуют главным напряжениям. Для определения направления главных площадок из точки проведем прямую параллельно оси до пересечения с окружностью в точке М, которая называется полюсом. Прямые, проведенные из полюса в точки А и В, соответствуют направлению главных напряжений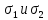соответственно.

Второй тип. Пусть известны главные напряжения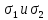. Требуется определить напряжения на площадках, направленных под углом 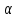к главным.

Решение. Вдоль оси 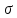(рис. 7.7, б) отложим отрезки ОА и ОВ, соответствующие главным напряжениям 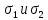. На отрезке АВ, как на диаметре, построим окружность напряжений Мора. Из центра окружности (точка С) отложим центральный угол 2α с осью σ и проведем прямую до пересечения с окружностью в точках D_α и D_β.

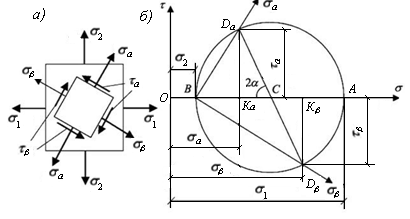
Рис. 7.7. Схема круга Мора для нахождения напряжений

на второстепенных площадках

Координаты этих точек соответствуют напряжениям на площадках, повернутых на угол 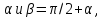и на площадке, на которой действует главное напряжение . Положения этих площадок получим, проведя из точки В прямые до пересечения с окружностью в точках .

7.7. Объемное напряженное состояние

В общем случае напряженного состояния на гранях элементарного параллелепипеда, выделенного в окрестности точки нагруженного тела, действует девять компонентов тензора напряжений. В силу закона парности касательных напряжений независимыми являются только шесть из них.

Вычислим напряжения на произвольной площадке ABC с вектором нормали ν в окрестности произвольной точки О (см. рис. 7.7). Обозначим направляющие косинусы вектора нормали ν к площадке ABC величинами:

Проекции полного напряжения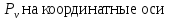, действующего на площадке АВС, обозначим 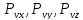. Для их определения составим уравнения равновесия четырехгранника, выделенного координатными плоскостями и плоскостью АВС в окрестности произвольной точки нагруженного тела (рис. 7.8):

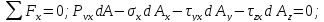
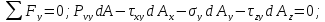
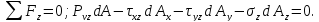
Площади граней элементов связаны между собой зависимостями:

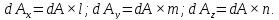
Учитывая это, получим:

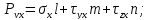
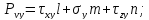
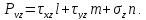
Нормальные напряжения найдем, составив сумму проекций на направление нормали:

Полное напряжение на площадке:

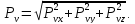
Касательное напряжение на площадке:

.

Определение главных напряжений.

Пусть площадка АВС (рис. 7.8) – главная, а нормаль к ней 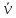совпадает с главной осью. Касательные напряжения на этой грани отсутствуют, а нормальное напряжение совпадает с полным. Проекции этого напряжения на координатные оси равны:

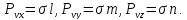
Учитывая выражение для , получим:

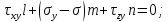
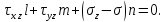
Эти равенства можно рассматривать, как однородную систему линейных алгебраических уравнений относительно l, m и n.

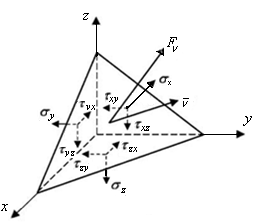
Рис. 7.8. Схема площадки для определения

главных напряжений

Так как направляющие косинусы связаны соотношениями l + m + n = 1, нулевое решение этой системы невозможно. Нулевое решение системы возможно только в том случае, когда определитель, составленный из ее коэффициентов при неизвестных, обращается в нуль, т. е.

.

Раскрыв этот определитель, получим кубическое уравнение относительно главного напряжения :

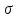где

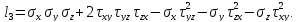
В силу симметрии определителя относительно главной диагонали, соответствующее ему кубическое уравнение имеет три действительных корня, три главных напряжения: .

Главные напряжения в точке нагруженного тела не зависят от выбора системы координат. Поэтому

и называют их соответственно первым, вторым и третьим инвариантами тензора напряжений. Их можно представить в виде:

;

;

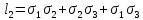В случае объемного напряженного состояния напряжения также можно представить графически. Если рассмотреть наклонные площадки, параллельные одному из главных напряжений, то для них справедливы формулы для плоского напряженного состояния. Из рис. 7.9 видно, что напряжение σ₃ не влияет на величину напряжений σ_α и τ_α, действующих на площадке, параллельной σ₃. Тогда напряжения на таких площадках можно представить графически, построив круг Мора на главных напряжениях σ₁ и σ₂. Аналогично можно представить графически напряжения на наклонных площадках, параллельных σ₁ и σ₂, как показано на рис. 7.10. Однако точки, расположенные на этих трех кругах, не исчерпывают всех наклонных площадок в точке нагруженного тела.

Рис. 7.9. Схема наклонной площадки при объемном

напряженном состоянии

Можно показать, что площадкам общего положения соответствуют точки на плоскости, лежащие в заштрихованной области между тремя кругами Мора. Точки, являющиеся вершинами этих кругов, соответствуют площадкам, наклоненным под углом 45^о к соответствующим главным площадкам.

Рис. 7.10. Круги Мора для определения

касательных напряжений

Касательные напряжения на этих площадках равны радиусам кругов Мора и определяются формулами:

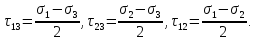
Максимальное касательное напряжение