5.6. Вычисление главных моментов инерции и определение положения главных центральных осей. Радиусы инерции

Подставив значение a_о в формулу J_x1 (J_у1), после преобразований получим формулу для определения главных моментов инерции:

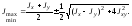
Главные оси, проходящие через центр тяжести сечения, называются главными центральными осями. Одна из главных осей инерции (ось максимум) обозначается U, а другая (ось минимум) – V (рис. 5.3).

Например, положение главной центральной оси U, относительно которой момент инерции максимален, т. е. I_U = I_max, можно определить двумя способами:

1) при J_xy < 0 главная ось U проходит через 1-й и 3-й, а при J_xy > 0 – через 2-й и 4-й квадранты;

2) если J_x > J_y, то главная ось U находится под углом α_о к оси x. При J_x < J_y ось U находится под углом α_о к оси y.

Радиусы инерции сечения относительно координатных осей x, y обозначаются i_x, i_y  соответственно и определяются по формулам:

; ,

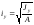где А – площадь поперечного сечения бруса.

5.7. Моменты инерции простых сечений

Определим осевые моменты инерции прямоугольника относительно осей x и y, проходящих через его центр тяжести. Выделим в плоскости прямоугольника элементарную площадку dА шириной b и высотой dy₁ (рис. 5.4).

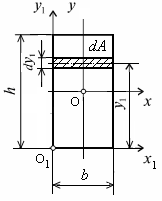
Рис. 5.4. Схема прямоугольника

для определения главных

осевых моментов инерции

Определим осевой момент инерции J_x1 относительно оси х₁, проходящей через основание прямоугольника:

,

аналогично

.

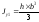Найдем осевой момент инерции J_x относительно оси х, проходящей через центр тяжести прямоугольника. Используем формулы для оп-

ределения осевого момента инерции при параллельном переносе осей:

аналогично

,

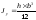где 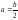– расстояние между осями у₁ и у;

– расстояние между осями х₁ и х;

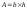– площадь прямоугольника.

Определим осевые моменты инерции треугольника. В плоскости треугольника (рис. 5.5) выделим элементарную площадку, параллельную оси х, площадью dA = b(y_i)  dy_i.

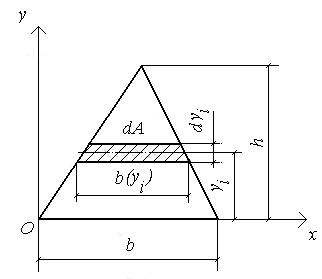
Рис. 5.5. Схема треугольника

для определения главных

осевых моментов инерции

Из подобия треугольников имеем:

.

Из этого соотношения находим 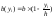, тогда , подставим dA в формулу для определения J_x, получим

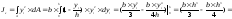
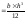, аналогично 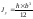– осевые моменты инерции треугольника относительно осей х и у соответственно.

Определим осевой момент инерции треугольника относительно центральной оси, параллельной основанию (рис. 5.6).

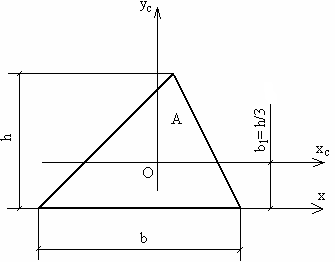
Рис. 5.6. Схема треугольника

для определения момента инерции

относительно центральной оси х_с

Воспользуемся формулой , откуда . Учитывая, что 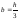, 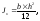окончательно получим

Определим полярный и осевые моменты инерции круга. В плоскости круга (рис. 5.7) выделим элементарную площадку в виде тонкого кольца с внутренним диаметром  и толщиной d. Тогда площадь кольца dА = 2d и полярный момент инерции круга

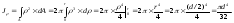Согласно зависимости имеем – осевой момент инерции круга.

Рис. 5.7. Схема круга для определения

полярного и осевых моментов инерции

5.8. Окружность инерции Мора

Практические задачи на вычисление моментов инерции относительно повернутых осей удобно решать графическим способом при помощи окружности инерции Мора.

Зависимости, полученные при повороте осей,

возведем в квадрат:

и сложим, получим

.

Обозначим 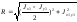, , 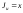, тогда полученное в результате сложения уравнение имеет вид – уравнение окружности, центр которой лежит на оси и смещен вправо от начала координат на величину а.

Таким образом, моменты инерции относительно повернутых осей определяются координатами точек некоторой окружности, которая называется окружностью инерции Мора.

Пусть требуется определить моменты инерции для некоторого произвольного сечения (рис. 5.8) относительно повернутых осей u и v, если известны моменты инерции относительно осей х₁ и у₁.

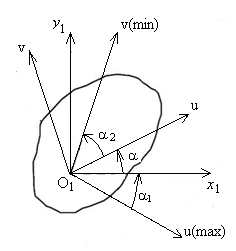
Рис. 5.8. Схема для определения

моментов инерции сечения

относительно повернутых осей u и v

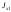
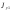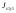
Предположим, что  ,  0. Откладывая осевые моменты инерции по оси абсцисс, а центробежные – по оси ординат, выполним следующие графические построения (рис. 5.9):

1) отложим в масштабе отрезки ОD = J_x1, DA = J_x1y1; ОЕ = J_y1, ЕВ = – J_x1y1, получим точки А и В;

2) на отрезке АВ, как на диаметре, построим окружность, которая является окружностью инерции Мора. Докажем это утверждение. Так как АО₁D = BО₁E, то

О₁D = O₁E = 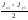; О₁А = О₁В = =

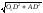= R,

OO₁ = OE + EO₁ = 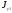+ = = 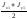a.

Рис. 5.9. Окружность инерции Мора

Согласно рис. 5.9, центр построенной окружности сдвинут вправо относительно начала координат на расстояние а и ее радиус равен радиусу окружности инерции Мора;

3) проведем из точки А горизонтальную прямую до пересечения с окружностью в точке С, которая называется полюсом окружности инерции Мора.

Полюс обладает следующим свойством. Если из полюса провести отрезок параллельно некоторой оси U, то он пересечет окружность инерции Мора в точке К, координаты которой равны моментам инерции: J_u = ОL, J_uv= КL.

Осевой момент инерции J_y определяется абсциссой точки М пересечения луча CM  CК с окружностью инерции Мора, т. е. J_v= ON, J_ху= –MN.

Окружность инерции Мора можно использовать для определения главных моментов инерции и положения главных осей. Главные моменты инерции на окружности изображаются точками 1 и 2, у которых ординаты равны нулю. Тогда имеем:

, .

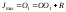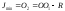Так как , , то окончательные формулы для определения главных моментов инерции имеют вид

.

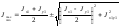Главные оси инерции определяются углами ₁, ₂ или ₀ (рис. 5.9):

;

;

,

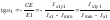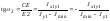где ₁, ₂ – углы, образованные осями U_max и V_min с осью X₁(J_ос) соответственно.