12.9. Задачи для самостоятельного решения

ЗАДАЧА №6

Определить наибольшую допускаемую величину сжимающей силы F на деревянную стойку круглого поперечного сечения диаметром d=200 мм при допускаемом напряжении [σ]=10 МПа. Длина стойки 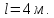Оба конца ее шарнирно оперты (рис.12.16).

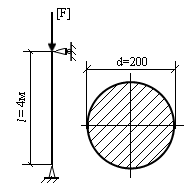
Рис. 12.16. Схема деревянной стойки

ОТВЕТ: [F] = 150кН

12.10. Контрольные вопросы

1. В чем заключается явление потери устойчивости сжатого стержня?

2. Какая сила называется критической силой?

3. Какое дифференциальное уравнение из теории изгиба лежит в основе вывода формулы Л. Эйлера?

4. Что называется гибкостью стержня? Приведите формулу.

5. Приведите формулу Л. Эйлера для определения критической силы?

6. Как учитывается различное закрепление концов стержня при определении критической силы?

7. Каков предел применимости формулы Л. Эйлера?

8. Как определяется предельная гибкость для формулы Л. Эйлера?

9. Как определяется критическая сила при напряжениях, превышающих предел пропорциональности материала?

10. Какой вид имеет график изменения критической силы в зависимости от гибкости (или длины) для стальных стержней?

11. Приведите формулу Ф. Ясинского для определения критической силы и укажите пределы её применимости.

12. Как определяется коэффициент запаса устойчивости сжато-

го стержня?

13. Напишите условие устойчивости сжатого стержня через критическую силу и коэффициент запаса устойчивости.

14. Напишите условие устойчивости сжатого стержня с помощью коэффициента продольного изгиба .

15. От чего зависит коэффициент продольного изгиба , и в каких пределах он изменяется?

16. Какие три типа задач можно решать исходя из условия устойчивости сжатого стержня?

17. Покажите порядок подбора сжатого стержня из условия устойчивости с помощью коэффициента .

13. Динамические нагружения

13.1. Виды динамических нагрузок. Учет сил инерции. Критическая скорость вращения вала

В предыдущих главах рассматривались случаи действия на тело статических нагрузок, которые прикладывались постепенно, без ускорений.

Рассмотрим действие динамической нагрузки, которая сравнительно быстро изменяет свою величину или положение (например, движущаяся машина, поезд).

Действие динамических нагрузок характеризуется наличием сил инерции, равных произведению массы тела на его ускорение и направленных в сторону, противоположную ускорению (I = ma). Силы инерции вызывают дополнительные напряжения и деформации, которые необходимо учитывать.

Общий метод расчета на динамическую нагрузку основан на принципе Даламбера. Согласно этому принципу всякое движущееся тело может рассматриваться в равновесии, если к действующим на него внешним силам добавить силу инерции. То есть если силы инерции известны, то внутренние усилия определяются обычным путем – методом сечений.

Рассмотрим задачу о расчете троса, поднимающего груз G с ускорением а (рис. 13.1).

Площадь поперечного сечения троса – А, объемный вес материала троса – γ.

Если груз находится в покое или поднимается равномерно, т. е. без ускорения (рис. 13.1, а), то на расстоянии z от груза продольная сила будет равна:

где 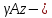вес участка троса длиной z.

Если груз поднимается с ускорением (рис. 13.1, б), возникает сила инерции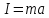, направленная вниз, значение которой определяется по формуле

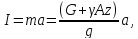
где g = 9,81 м/с² – ускорение свободного падения.

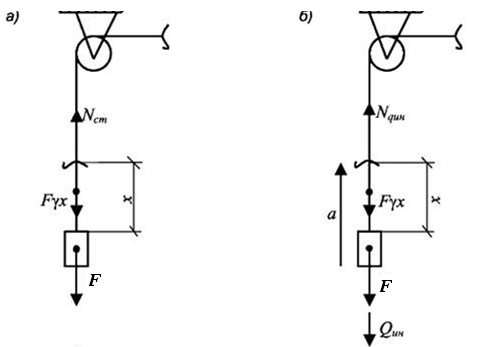
Рис. 13.1. Схема поднимаемого с ускорением груза

Тогда получим:

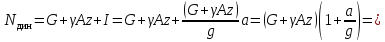
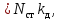
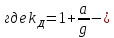динамический коэфициент.

Определим динамическое напряжение:

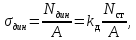
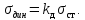
Если груз опускается с ускорением а, то величина ускорения будет входить в формулу усилия и напряжения со знаком «минус». При свободном падении груза при 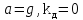, т. е. трос будет следовать за грузом без натяжения,.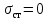

Расчетная модель вала.

1. С точки зрения формы: прямой брус, работающий на кручение или на сложное сопротивление – кручение с изгибом, постоянного и переменного поперечного сечения по длине.

2. С точки зрения материала: материал вала рассматривается как однородный и изотропный по длине. Деформации, возникающие в поперечном сечении вала, малы по сравнению с размерами самого вала.

3. С точки зрения нагружения: вал рассчитывается на статическую нагрузку, которая медленно возрастает от нуля до конечного значения, а затем не изменяется со временем. В зависимости от установленного числа шкивов, числа зубчатых пар и т. д. вал рассчитывается с одной или несколькими сосредоточенными массами.

4. С точки зрения разрушения: вал рассчитывается на длительное статическое разрушение, которому предшествуют только упругие деформации.

Кроме того, при расчете вала необходимо учитывать:

- место расположения подшипников. В зависимости от их расположения валы делятся на однопролетные и консольные (рис. 13.2);

- соотношение между собственной скоростью вращения вала и критической. В зависимости от этого валы разделяются на тихоходные (жесткие), при этом 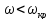, и быстроходные (гибкие) – .

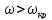Рис. 13.2. Схемы валов в зависимости от опорных закреплений

Из практики эксплуатации машин известно, что вал при некоторых определенных числах оборотов, попадая в резонанс, становится динамически неустойчивым. При этом в поперечном сечении вала возникают недопустимые поперечные колебания вала.

Число оборотов вала, при котором вал переходит в резонанс, называется критическим (рис. 13.3).

Колебания и вибрация обусловлены эксцентриситетом между центрами тяжести сечения вала и насадками (шкив, шестерня и т. д.) на вал в данном сечении.

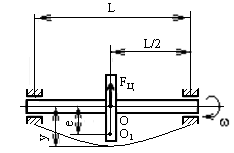
Рис. 13.3. Схема вала для определения

критических оборотов

О₁ – центр тяжести шкива;

О – центр тяжести вала;

е – эксцентриситет между центрами тяжести вала и шкива (несовпадение центров тяжести масс вала и шкива);

у – прогиб вала.

Прогиб вала определяется по формуле

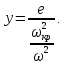
Из данного выражения следует:

1) если собственная скорость вращения вала меньше критической скорости, то прогиб вала не выходит за пределы допускаемого;

2) при стремлении собственной скорости вращения вала к критической амплитуда колебаний уменьшается, но прогиб вала увеличивается до бесконечности, что может привести к разрушению;

3) в том случае, если собственная скорость вращения больше критической, то прогиб вала уменьшается. При этом центр массы шкива приближается к оси опор подшипников и несбалансированный шкив самоцентрируется, т. е. превышение собственной скорости над критической скоростью вращения соответствует работоспособности вала.

Таким образом, вывод вала из состояния резонанса можно обеспечить за счет динамической или статической балансировки или за счет обеспечения неравенства собственной скорости вращения и критической. Поэтому при расчете вала на виброустойчивость используются следующие соотношения:

для жестких валов:

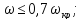
для гибких валов:

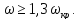
Расчет критической скорости вращения вала проводят с учетом следующих условий:

а) критическая скорость вала без учета массы вала (учитывается только масса сосредоточенных на валу масс):

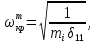
где 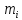– масса устанавливаемого на вал элемента;

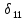– коэффициент влияния или коэффициент приведения, который зависит от расположения на валу масс и расположения подшипников (рис. 13.4);

б) критическая скорость с учетом собственной массы вала:

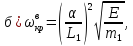
где J_x – осевой момент инерции сечения вала относительно оси x;

α – корень решения уравнения изменения критической скорости от массы.

Рис. 13.4. Схемы однопролетного и консольного валов

Критическая скорость с учетом массы самого вала и массы, установленной на валу, определяется по формуле

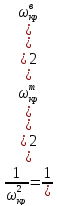
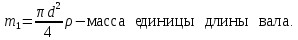
При выборе жесткого или гибкого вала необходимо учитывать отношение рабочей скорости вращения к критической, т. е.

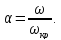
При этом следует помнить, что:

- уменьшение диаметра вала уменьшает деформацию, и, следовательно, уменьшает критическую скорость;

- увеличение длины вала уменьшает критическую скорость вращения;

- смещение массы на валу от центра вдоль оси уменьшает критическую скорость вращения;

- увеличение вылета центра вращающихся масс уменьшает критическую скорость вращения;

- введение упругих опор уменьшает критическую скорость вращения.