7.8. Деформированное состояние

Под действием внешних сил элементы конструкций и машин изменяют свои первоначальные размеры и форму. Эти изменения характеризуются деформациями и перемещениями тела. Перемещения упругих тел могут быть двух видов: а) перемещения как абсолютного твердого тела; б) перемещения отдельных точек тела, обусловленные деформациями материала. В механике материалов рассматриваются конструкции, в которых возникающие в них перемещения вызваны деформациями тела.

Для исследования деформированного состояния рассмотрим элемент ABCD (рис. 7.11), который после деформации тела перешел в состояние А^′B^′C^′D^′. Переход от начального состояния в конечное может быть осуществлен за счет изменения длины сторон (без изменения углов между ними) и за счет изменения углов (без изменения длин).

Пусть до деформации длина элемента АВ была равна dx, а АС – dy, угол между ними равен 90°, и ориентированы они в направлении осей Ох и Оу соответственно (рис. 7.12). Пусть после деформации точки А, В и С заняли положение А^′, В^′, С^′. Перемещения точки А в направлении оси Ох равно u, оси Оу – v, а перемещения точек В и С соответственно:

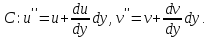
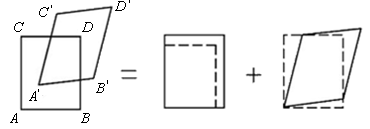
Рис. 7.11. Схема деформации элемента твердого тела

Тогда линейные деформации элементов АВ и АС определяются в виде:

.

Угловые деформации, т. е. изменение углов и 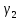(рис. 7.12), равны:

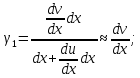
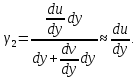
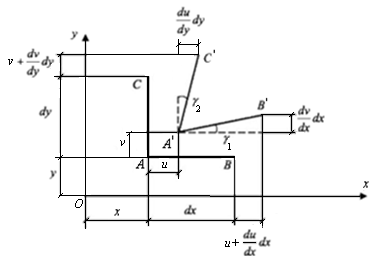
Рис. 7.12. Схема для определения линейных

и угловых деформаций элемента

Угол сдвига между элементами АВ и АС:

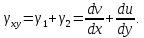
При выводе этих соотношений учитывалось, что перемещения и углы поворота малы, т. е.

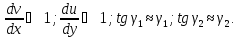
Аналогично линейные деформации в направлении оси z и углы сдвига в плоскостях x и определяются по формулам:

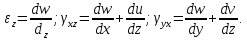
Таким образом, деформированное состояние характеризуется величинами 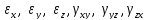, а выражения, связывающие их с компонентами вектора перемещений u, v, w, называются соотношениями Коши.

Часто при исследовании деформаций необходимо определить линейную деформацию в направлении, составляющем угол с осью Ох. Рассмотрим отрезок АВ, который деформируетcя в плоскости хОу и занимает положение 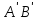(рис. 7.13). Компоненты вектора перемещения точки A в направлении осей Ох и Оу равны u, v и точки В:

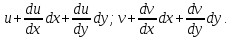
Длина отрезка АВ до деформации равна ds, а после деформации:

Тогда деформация отрезка АВ в направлении, определяемом углом 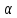, равна:

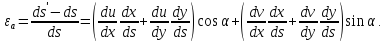
Учитывая, что

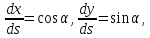
из соотношения Коши получим:

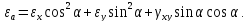
Рис. 7.13. Схема для определения деформации

элемента в направлении угла α

Если заменить на 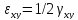, то эта формула будет полностью совпадать с выражением для 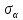. Таким образом, деформация в точке характеризуется тензором деформаций:

Как и тензор напряжений, его можно привести к диагональному виду:

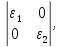
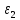где и – главные деформации.

Аналогично объемная деформация в точке определяется тензором деформаций, который можно представить в общем или диагональном виде:

Вычислим относительно объемную деформацию тела. Для этого рассмотрим элементарный параллелепипед. Размеры сторон его до деформации равны dx, dy, dz. После деформации их размеры равны 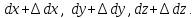Начальный объем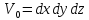, а после деформации:

Раскрыв скобки и учитывая, что деформации малы, т. е. пренебрегая произведениями , найдем относительное изменение объема:

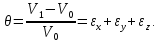
Таким образом, 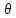является первым инвариантом тензора деформаций.