
- •20.06.2012 Г. (протокол № 10)
- •11.06.2012 Г. (протокол № 10)
- •Введение
- •1. Основные определения, методы и принципы механики материалов
- •1.1. Задачи, цель и предмет механики материалов
- •1.2. Краткая история развития науки о механике материалов
- •1.3. Расчетная схема. Типовые формы элементов
- •1.4. Внешние силы и их классификация
- •1.5. Основные гипотезы и принципы механики материалов
- •1.6. Контрольные вопросы
- •2. Внутренние силы и усилия. Метод сечений
- •2.1. Понятие о внутренних силах и напряжениях
- •2.2. Внутренние усилия
- •2.3. Выражение внутренних усилий через внешние силы
- •2.4. Контрольные вопросы
- •3. Механические характеристики материалов
- •3.1. Испытание материалов на растяжение
- •3.2. Пластическое и хрупкое разрушение материалов
- •3.3. Концентрация напряжений
- •3.4. Расчеты элементов конструкций (сооружений) на прочность по допускаемым напряжениям и нагрузкам. Коэффициент запаса прочности
- •3.5. Контрольные вопросы
- •4. Растяжение и сжатие
- •4.1. Деформации при растяжении и сжатии
- •4.2. Напряжения при растяжении и сжатии
- •4.3. Абсолютная и относительная деформации. Закон Гука. Коэффициент Пуассона
- •4.4. Условия прочности и жесткости
- •4.5. Потенциальная энергия упругой деформации
- •4.6. Пример расчета
- •4.7. Статически неопределимые системы
- •4.7.1. Определение монтажных напряжений, вызванных технологическими неточностями
- •4.7.2. Определение температурных напряжений
- •4.8. Задачи для самостоятельного решения
- •4.9. Контрольные вопросы
- •5. Геометрические характеристики поперечных сечений бруса
- •5.1. Статические моменты площади сечения
- •5.2. Определение центра тяжести сечения
- •5.3. Осевой, центробежный и полярный моменты инерции сечения. Общие свойства
- •5.4. Изменение моментов инерции при параллельном переносе и повороте осей
- •5.5. Главные оси и главные моменты инерции
- •5.6. Вычисление главных моментов инерции и определение положения главных центральных осей. Радиусы инерции
- •5.7. Моменты инерции простых сечений
- •5.8. Окружность инерции Мора
- •5.9. Моменты сопротивления сечений
- •5.10. Пример расчета
- •5.11. Задачи для самостоятельного решения
- •5.12. Контрольные вопросы
- •6. Сдвиг
- •6.1. Основные понятия о деформации сдвига. Абсолютный и относительный сдвиг
- •6.2. Внутренние усилия при деформации сдвига. Напряжения при сдвиге. Закон Гука при сдвиге. Модуль сдвига
- •6.3. Связь между модулями упругости e и g для изотропного тела
- •6.4. Расчет на прочность при сдвиге. Потенциальная энергия деформации при сдвиге
- •6.5. Практические примеры деформации сдвига – расчет заклепочных и болтовых соединений на срез и смятие.
- •6.6. Пример расчета
- •6.7. Контрольные вопросы
- •7.2. Закон парности касательных напряжений
- •7.3. Главные площадки и главные напряжения
- •7.4. Линейное напряженное состояние
- •7.5. Плоское напряженное состояние
- •7.6. Круг напряжений Мора
- •7.7. Объемное напряженное состояние
- •7.8. Деформированное состояние
- •7.9. Обобщенный закон Гука
- •7.10. Потенциальная энергия деформации
- •7.11. Пример расчета
- •7.12. Контрольные вопросы
- •8. Теория прочности
- •8.1. Назначение и сущность теорий прочности. Эквивалентное напряженное состояние и эквивалентное напряжение
- •8.2. Критерий наибольших нормальных напряжений (первая теория прочности)
- •8.3. Критерий наибольших линейных деформаций (вторая теория прочности)
- •8.4. Критерий наибольших касательных напряжений (третья теория прочности)
- •8.5. Критерий удельной потенциальной энергии формоизменения (четвертая теория прочности)
- •8.6. Теория прочности Мора
- •8.7. Пример расчета
- •8.8. Задачи для самостоятельного решения
- •8.9. Контрольные вопросы
- •9. Изгиб
- •9.1. Общие сведения об изгибе балок. Виды изгиба. Чистый изгиб. Поперечный изгиб. Допущения
- •9.2. Внутренние силовые факторы при изгибе. Нормальные напряжения при изгибе. Эпюры напряжений
- •9.3. Построение эпюр изгибающего момента м и поперечной силы q при изгибе
- •9.4. Дифференциальные зависимости при изгибе. Контроль правильности построения эпюр
- •9.5. Касательные напряжения при изгибе. Эпюры напряжений
- •9.6. Условия прочности при изгибе по нормальным и касательным напряжениям
- •9.7. Рациональные формы поперечного сечения балок
- •9.8. Главные напряжения при изгибе
- •9.9. Деформации при изгибе. Угол поворота и прогиб сечения. Дифференциальное уравнение изогнутой оси балки
- •9.10. Способы определения перемещений при изгибе
- •С помощью интеграла Мора
- •Верещагина
- •9.11. Балки переменного сечения. Определение деформаций
- •, Откуда ;
- •, Откуда .
- •9.12. Расчет статически неопределимых балок.
- •Промежуточного шарнира
- •9.13. Пример расчета
- •9.14. Контрольные вопросы
- •10.2. Угол закручивания. Главные напряжения. Потенциальная энергия упругой деформации при кручении
- •10.3. Расчет на прочность и жесткость круглого и кольцевого поперечного сечения. Расчет валов по заданной мощности и частоте вращения
- •10.4. Статически неопределимые задачи на кручение
- •10.5. Расчет цилиндрических винтовых пружин с малым шагом витков
- •10.6. Пример расчета
- •10.7. Задачи для самостоятельного решения
- •10.8. Контрольные вопросы
- •11. Сложное сопротивление
- •11.1. Особенности расчета брусьев при сложном сопротивлении
- •11.2. Косой изгиб, основные понятия. Нормальные напряжения в поперечных сечениях бруса. Нахождение опасного сечения
- •11.3. Положение нейтральной оси и опасных точек
- •11.4. Внецентренное растяжение и сжатие бруса. Нормальные
- •11.5. Нейтральная ось, ее уравнение и свойства
- •11.6. Положение опасных точек. Условие прочности
- •11.7. Понятие о ядре сечения при внецентренном растяжении
- •11.8. Изгиб с кручением пространственного вала
- •11.9. Определение положения опасного сечения и диаметра вала с использованием третьей и четвертой теорий прочности
- •11.10. Пример расчета
- •11.11. Контрольные вопросы
- •12.2. Критическая сила. Формула Эйлера. Влияние закрепления концов стержня на величину критической силы
- •12.3. Пределы применимости формулы Эйлера. Потеря устойчивости при напряжениях, превышающих предел пропорциональности. Формула Ясинского
- •12.4. Расчеты сжатых стержней на устойчивость при помощи коэффициента уменьшения основного допускаемого напряжения на сжатие
- •12.5. Выбор материалов и рациональной формы поперечных сечений сжатых стержней
- •12.7. Пример расчета
- •12.9. Задачи для самостоятельного решения
- •12.10. Контрольные вопросы
- •13. Динамические нагружения
- •13.1. Виды динамических нагрузок. Учет сил инерции. Критическая скорость вращения вала
- •13.2. Элементарная теория удара. Динамический коэффициент. Продольный и поперечный удар
- •13.3. Удар при кручении. Защита приборов и оборудования от ударов. Определение напряжений при ударном воздействии
- •13.4. Пример расчета
- •13.5. Задачи для самостоятельного решения
- •13.6. Контрольные вопросы
- •Приложения
- •Двутавры стальные горячекатаные (по гост 8239–89)
- •Швеллеры стальные горячекатаные (по гост 8240–89)
- •Уголки стальные горячекатаные равнополочные (по гост 8509–86)
- •Уголки стальные горячекатаные неравнополочные (по гост 8510–86)
- •Коэффициент снижения основного допускаемого напряжения φ при продольном изгибе
4.3. Абсолютная и относительная деформации. Закон Гука. Коэффициент Пуассона
Выделим из стержня на участке, где действует постоянная продольная сила N, некоторую его часть длиной l и шириной b (см. рис. 4.3, а). Опыты показывают, что при растяжении резинового стержня его длина увеличивается, а ширина уменьшается. Пусть l1 и b1 – длина и ширина стержня после деформации соответственно.
Изменение длины стержня при растяжении (сжатии) называется абсолютной продольной деформацией и определяется по формуле
∆l = l1 – l2.
Отношение абсолютной продольной деформации к первоначальной длине стержня называется относительной продольной деформацией и определяется по формуле
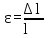 .
.
По аналогии с продольными деформациями имеем:
∆b = b1 – b, ∆h = h1 – h – абсолютные поперечные деформации;
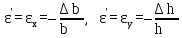 – относительные
поперечные деформации.
– относительные
поперечные деформации.
При растяжении: N 0, ∆l 0, ε 0, ∆b < 0, ε' < 0; при сжатии: N < 0, ∆l < 0, ε < 0, ∆b 0, ε' 0.
Закон Гука – относительная продольная деформация прямо пропорциональна нормальному напряжению, а именно:
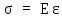 ,
,
где Е – модуль Юнга или модуль упругости первого рода (кН/см2, МПа).
Используя
зависимости
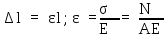 ,
получим
,
получим
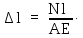
Абсолютная продольная деформация прямо пропорциональна продольной силе в пределах участка длиной l при постоянных N и EА, где EА – жесткость поперечного сечения при растяжении (сжатии).
Коэффициент Пуассона – безразмерная величина, характеризующая упругие свойства и способность материала деформироваться в поперечном направлении при его растяжении или сжатии в продольном направлении.
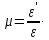
Для реальных материалов коэффициент Пуассона изменяется в очень узких пределах: = 0…0,5.
Значение для некоторых материалов:
-
пробка –
 ;
;
-
резина –
 ;
;
-
сталь –
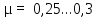 ;
;
-
свинец –
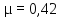 ;
;
-
бетон –
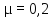 ;
;
- каучук – 0,5.
Значение коэффициента Пуассона определяется опытным путем в результате специальных испытаний материала.
4.4. Условия прочности и жесткости
Условие прочности элементов конструкций и сооружений рассмотрено в главе 3.
В некоторых случаях для обеспечения нормальной работы машин, конструкций и сооружений требуется проектировать размеры деталей и элементов таким образом, чтобы обеспечивалось условие жесткости:
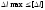 ,
,
где
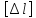 – допускаемое удлинение, задается
техническими условиями.
– допускаемое удлинение, задается
техническими условиями.
Удлинение ступенчатых стержней, а также когда внешние силы приложены в разных точках продольной оси стержня, определяется суммированием удлинений отдельных участков.
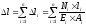 ,
,
где Ni, li, Ei, Аi – нормальная сила, длина, модуль упругости и площадь поперечного сечения і-го участка соответственно.
Условие жесткости позволяет выполнять три вида расчетов:
1)
проверочный:
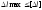 ;
;
2)
проектировочный: 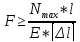
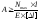 (стержень
постоянного сечения);
(стержень
постоянного сечения);
3) расчет грузоподъемности или несущей способности:
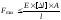 .
.
4.5. Потенциальная энергия упругой деформации
Внешние силы, приложенные к упругому телу и вызывающие изменение его геометрии, совершают работу АF на соответствующих перемещениях. В упругом теле накапливается потенциальная энергия деформации U. При действии динамических нагрузок часть работы внешних сил превращается в кинетическую энергию движения частиц тела К.
Уравнение баланса энергии можно записать в следующем виде:
АF = U + K.
При статическом нагружении упругого тела работа внешних сил полностью преобразуется в потенциальную энергию деформации, следовательно, АF = U. При разгрузке тела производится работа за счет потенциальной энергии деформации, накопленной телом. При этом упругое тело является аккумулятором энергии. Это свойство упругого тела широко используется в заводных пружинах часовых механизмов, в конструкции лука и т. д. Для вывода необходимых расчетных зависимостей потенциальной энергии деформации рассмотрим простейший случай – растяжение стержня.
На рис. 4.5, а изображен стержень, растягиваемый силой F, удлинение которого соответствует l. График изменения величины удлинения стержня l в зависимости от силы F показан на рис. 4.5, б. В соответствии с законом Гука этот график носит линейный характер.
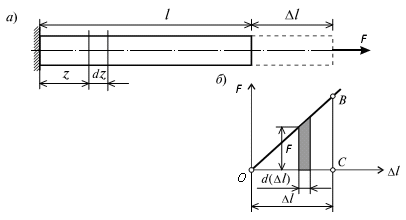
Рис. 4.5. а – схема растягиваемого стержня; б – график зависимости F – ∆l
Пусть некоторому значению силы F соответствует удлинение стержня l. Дадим некоторое приращение силе F соответствующее приращение удлинения составит d (l ). Элементарная работа на этом приращении удлинения составит:
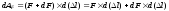 .
.
Вторым слагаемым, в силу его малости, можно пренебречь, и тогда
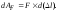
Полная работа равна сумме элементарных работ, тогда при линейной зависимости работа внешней силы F на перемещении l будет равна площади треугольника ОСВ (рис. 4.5, б), т. е.
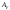
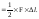
Если напряжения и деформации распределены по объему тела V равномерно, то потенциальную энергию деформации стержня можно записать в следующем виде:
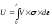 ,
,
где V = А l, F = A, = Е ;
А – площадь поперечного сечения стержня.
Тогда окончательно
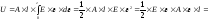
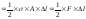 .
.
С
учетом
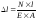 для
однородного стержня с постоянным
поперечным сечением при F = const
получим:
для
однородного стержня с постоянным
поперечным сечением при F = const
получим:
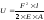 .
.
