0. 1.3. Оценивание параметров периодических сигналов по экспериментальным данным

При малом уровне помех метод наименьших квадратов может эффективно использоваться для разложения периодических функций в ряд Фурье, а также для оценивания коэффициентов ортогональных полиномов и различных ортогональных функций, в частности, полиномов Чебышева, Лежандра и др.

Ряды Фурье широко используются в настоящее время для решения важных практических задач. Например, в электроэнергетических системах наиболее эффективно передавать энергию при номинальных значениях частоты и напряжения. Однако в реальных условиях в энергосистемах возникают искажения синусоидальной формы кривых тока и напряжения. По­этому необходимо отклонения форм кривых тока и напряжения от правильной синусоидальной формы оценивать по гармоническим составляю­щим периодических сигналов.

Предположим, что в процессе обработки периодического сигнала получены значения напряжения через каждые 15° в контрольных точках. Измерения произведены с точностью, определяемой лишь одним знаком после запятой. Полученные данные в интервале изменения угла alf= 0°180° сведены в таблицу 1.2, содержащую 13 экспериментальных точек.

Таблица 1.2.

аlf(i) (град)	0	15	30	45	60	75	90	105	120	135	150	165	180
u(i)(B)	12.7	33.8	52.0	60.9	57.8	45.7	31.1	20.1	15.6	15.1	13.0	4.2	-12.7

B первой строке таблицы приведен угол alf(i) (в градусах), во вто­рой - напряжение u(i) (в вольтах), i = 0, . . . , 12 .

Требуется по данным таблицы 1.2. определить амплитуды и фазы первых трех гармони периодического сигнала

(1.22)

где ₀ - частота первой гармоники.

Таким образом, требуется оценить амплитуды и фазы

U1m , Q1 ,

U2m , Q2 ,

U3m , Q3 .

Разделив период t на 24 равных интервала, мы получим . Так как , то каждому будет соответствовать угол (в градусах).

.

Для нахождения угла в i-ой точке, где i= 024, можно воспользо­ваться простым соотношением

i = 0, …, 12,

на основании которого заполнена первая строка таблицы 1.2.

Из данных второй строки образуем вектор выхода

y₁ = [12.7 33.8 52.0 … 4.2 -12.7]^T

размерности (13Ч1).

Чтобы придать уравнению (1.22) вид модели (1.19), воспользуемся тождественным преобразованием

(1.23)

Введем обозначения

Эти величины в уравнении (1.23) являются постоянными. u(₀ t) является скалярной величиной. Она может быть получена в виде произве­дения двух векторов: вектор-строки [sin₀ t cos ₀ t sin 2₀ t cos 2₀ t sin 3₀ t cos 3₀ t] и вектор-столбца х, образованного из элементов

x = [x(1) x(2) x(3) x(4) x(5) x(6)]^T , т.е

u(₀ t) =[sin₀ t cos ₀ t sin 2₀ t cos 2₀ t sin 3₀ t cos 3₀ t]

Вектор x является искомым вектором, содержащим шесть неизвест­ных коэффициентов. Для их оценивания, согласно (1.10), требуется соста­вить число уравнений т > 6. Мы выбрали т = 13 и привели эти данные в таблице 1.2.

C помощью вектор-строки приведенного выше уравнения сформиру­ем матрицу H размерности (13Ч6), где каждая i-ая строка должна содер­жать значения элементов, соответствующие углу alf(i), приведенному в i- ой ячейке первой строки таблицы. B среде MatLAB эта операция выполня­ется в режиме прямых вычислений

alf=0:15:180;

bet = alf.*(pi/180);

H = [sin(bet)' cos(bet)' sin(2*bet)' cos(2*bet)'

sin(3*bet)' cos(3*bet)']

H =

0 1.0000 0 1.0000 0 1.0000

0.2588 0.9659 0.5000 0.8660 0.7071 0.7071

0.5000 0.8660 0.8660 0.5000 1.0000 0.0000

0.7071 0.7071 1.0000 0.0000 0.7071 -0.7071

0.8660 0.5000 0.8660 -0.5000 0.0000 -1.0000

0.9659 0.2588 0.5000 -0.8660 -0.7071 -0.7071

1.0000 0.0000 0.0000 -1.0000 -1.0000 0.0000

0.9659 -0.2588 -0.5000 -0.8660 -0.7071 0.7071

0.8660 -0.5000 -0.8660 -0.5000 0.0000 1.0000

0.7071 -0.7071 -1.0000 0.0000 0.7071 0.7071

0.5000 -0.8660 -0.8660 0.5000 1.0000 0.0000

0.2588 -0.9659 -0.5000 0.8660 0.7071 -0.7071

0.0000 -1.0000 0.0000 1.0000 0.0000 -1.0000

>>

Можно убедиться, что H имеет полный ранг: rank(Н)=6. Поэтому существует ее обратная матрица . Следовательно, для оценки x можно использовать уравнение (1.15).

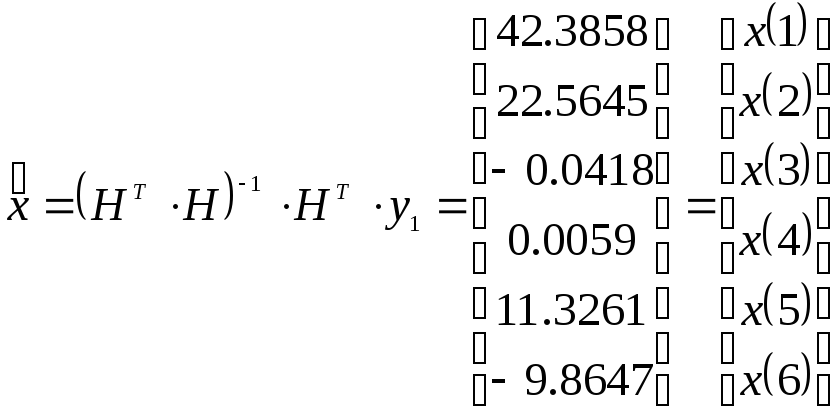
Используя выражения для x(l) и x(2), определим амплитуду первой гармоники U_1m и фазу Q₁

Угол Q₁ (в градусах) найдем с помощью уравнения

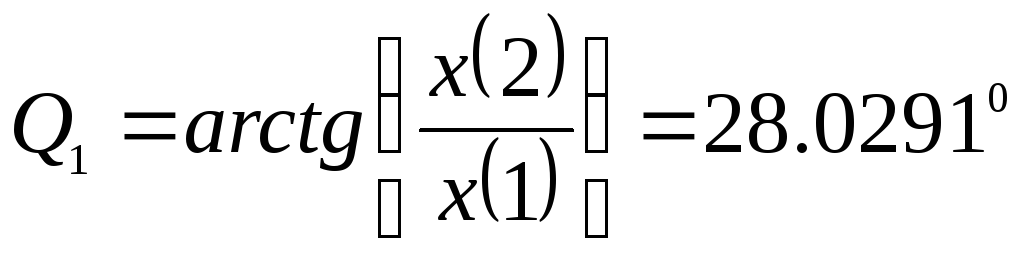
Аналогично определим U_2m, Q₂, U_3m и Q₃

Следовательно, напряжение u(₀ t), в соответствии с (1.22), может быть записано с помощью уравнения

(1.24)

при условии, что ₀ t имеет размерность "градусы".

B полученном уравнении (1.24) амплитуда напряжения первой гар­моники более чем на два порядка превышает амплитуду второй гармоники. Поэтому при выполнении инженерных расчетов второй гармоникой можно пренебречь, а в величинах аргументов первой и третьей гармоник - учесть лишь десятые доли градуса. Тогда получим

(1.25)

Все приведенные выше расчеты в среде MaiLAB могут быть выпол­нены в режиме прямых вычислений, без составления машинных программ. B случае автоматизации вычислительного процесса необходимо иметь в виду, что в составе вектора x* могут быть элементы равные нулю. Если, например, (3)и (4)равны нулю, то при получении U_2m=0 из цикла должна исключаться операция расчета Q₂, поскольку будет представлять собой неопределенность типа 0/0, и последующие вычисления на ПЭВМ прекратятся.

Чтобы оценить погрешность вычислений, вызванную ограничением разрядов чисел, содержащихся во второй строке таблицы 1.2, возвратим­ся к уравнению (1.26) — модели процесса, которая в действительности ис­пользована для получения экспериментальных данных и составления таблицы:

(1.26)

Видно, что вторая гармоника в составе сигнала отсутствовала. Повы­сим точность измерений и представим вектор у следующими данными:

y = [l2.6937 33.7823 52.0270 60.8661 57.8116 45.7234 ...

31.0608 20.1415 15.5952 15.0802 12.9958 4.1658 -12.6937]Т

B этом случае у условно можно считать вектором детерминирован­ных сигналов.

Чтобы убедиться практически в отсутствии шума в элементах у, оце­ним вновь искомые величины с помощью метода наименьших квадратов. B результате получим

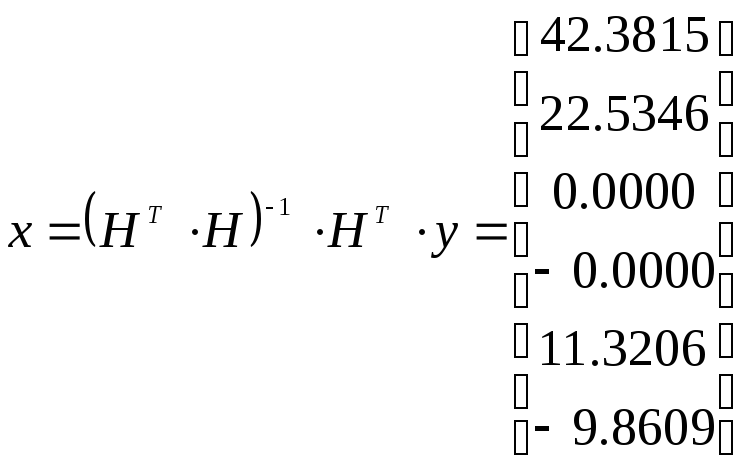(1.27)

Используя элементы вектора-столбца (1.27) для оценки амплитуд и фаз гармоник, будем иметь

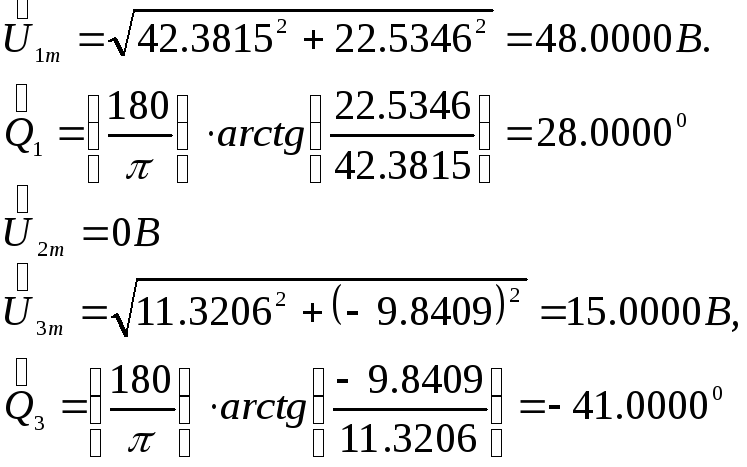
Таким образом, оценочные значения практически совпадают с при­нятыми исходными данными.

Теперь определим вектор шума z, представляющий собой разность между у и у₁:

z = y – y₁ = [-0.0063 -0.0177 0.0270 -0.0339 0.0116 0.0234 ...

-0.0392 0.0415 -0.0048 -0.0198 -0.0042 -0.0342 0.0063]^T

Для оценки z используем критерий (1.13)

Аналогичный результат получим, если воспользуемся эвклидовой нормой согласно правилу (1.18). Вычисления в среде MatLAB выполним с помощью оператора

Заметим, что полученные величины J не характеризуют "качество" моделирования. Адекватность модели и объекта, представленного векто­ром y₁, может быть установлена по вектору z₁, где

z₁ = y₁ – y_м= [-0.0056 0.0166 -0.0271 0.0309 -0.0150 -0.0223 ...

0.0462 -0.0330 0.0660 0.0091 -0.0166 0.0153 -0.0061]^Т

Вектор у_м, в свою очередь, следует восстановить, используя матрицу H и вектор наилучшей оценки

y_м = = [l2.7056 33.7834 52.0271 60.8691 57.8150 45.7223 ...

31.0538 20.1330 15.5934 15.0909 13.0166 4.1847 -12.6939]^T