5.2. Об аналитическом решении дифференциальных уравнений

С появлением эффективных вычислительных и программных средств моделирования переходных процессов в электрических цепях и системах может показаться, что роль классических приемов решения дифференциальных уравнений как в учебном процессе, так и научных исследованиях несколько снижается. Однако это не так. Если имеется возможность получить решение в аналитическом виде, то тем самым определяется модель для целого класса систем. Аналитическая модель является обобщающей. Поведение модели будет зависеть от конкретных параметров, характера воздействия внешних возмущений и др. Однако закономерность поведения моделируемой системы определяется классом модели, то есть аналитическим решением. Вычислительные средства здесь играют лишь вспомогательную роль. Они позволяют ускорить процесс вычислений, свободно варьировать параметры модели, визуально наблюдать протекание процессов на экране дисплея и др. средствах отображения информации, быстро рассчитывать параметры устройств управления, анализировать устойчивость и т.п. Мощные программные оболочки позволяют высвободить пользователя из рутинной среды программирования, но они не заменяют его как специалиста, создающего эффективные модели на базе новых технологий.

В электрических цепях и системах с сосредоточенными параметрами мы можем моделировать динамические процессы с помощью дифференциальных уравнений с постоянными коэффициентами. Получение решения уравнений этого класса изучается в курсах математики. Мы остановимся лишь на изложении некоторых рекомендаций, облегчающих процедуру поиска решения в аналитической форме и ведущих к упрощению математических преобразований.

Рассмотрим сначала дифференциальное уравнение второго порядка:

, (5.0)

где , и – постоянные коэффициенты.

Решение дифференциального уравнения состоит из суммы общего и частного решений. В теории электрических цепей общее решение обычно называется свободной составляющей, а частное – принужденной составляющей основной переменной состояния.

Общее решение (5.3) содержит две произвольные постоянные, которые определяются либо с помощью двух начальных условий (задача Коши), либо расщепленных (краевых) условий, задаваемых в начале и конце переходного процесса: и . В этом случае задача называется краевой.

Вид общего решения дифференциального уравнения определяется корнями характеристического уравнения, которые численно совпадают с собственными значениями матрицы , если (5.3) записать в матричной форме. Характеристическое уравнение имеет вид:

(5.0)

Рассмотрим три возможных случая:

1. Если корни и 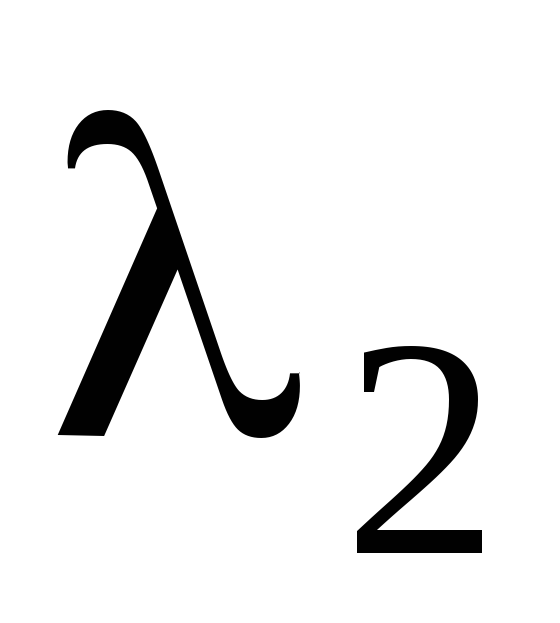в уравнении (5.4) вещественные и различные, то:

, (5.0)

где и – произвольные постоянные, определяемые из начальных условий.

2. Если и 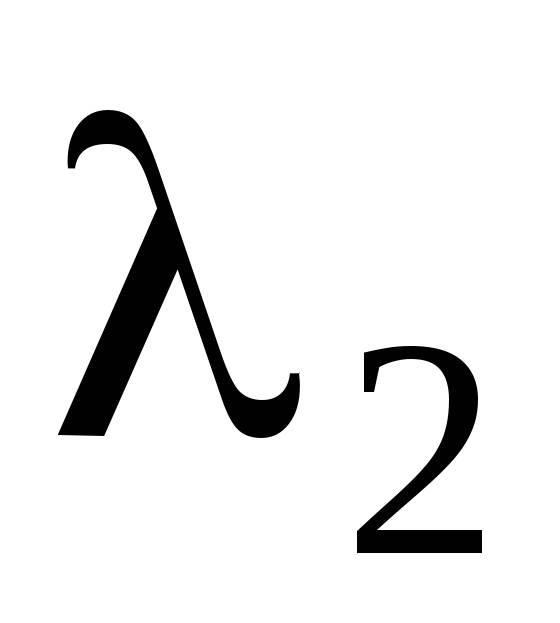– действительные и равные, то есть , то

(5.0)

3. Корни и уравнения (5.4) комплексно-сопряженные: , где и – действительные числа, 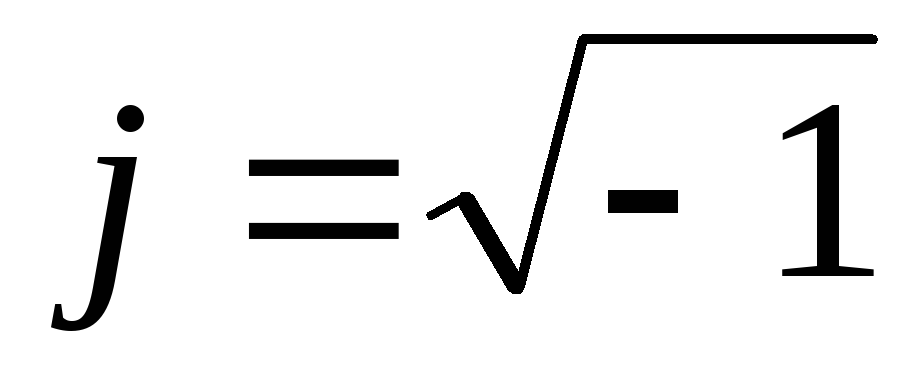– мнимое число. Решение имеет вид:

(5.0)

Обозначим частное решение неоднородного уравнения (5.3) через . Тогда решение (5.3) будет состоять из суммы:

(5.0)

Рассмотрим некоторые рекомендации по определению .

1. Функция 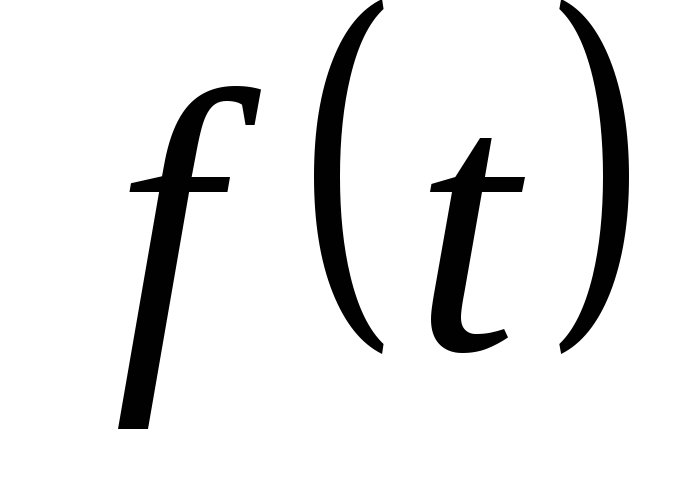в правой части (5.3) представляет собой полином степени :

(5.0)

где все – постоянные, – целое положительное число.

Частное решение следует искать также в форме полинома -ой степени:

(5.0)

Постоянные коэффициенты можно найти следующим образом. В левую часть уравнения (5.3) необходимо подставить выражение (5.10), а также первую и вторую производные (5.10) по времени. В правой части необходимо записать выражение (5.9). После группирования членов, содержащихся при одинаковых степенях (при ) слева от знака равенства, необходимо их приравнять коэффициентам при тех же , находящихся справа от знака равенства. В результате получим алгебраических уравнений, позволяющих вычислить значения .

Пример. Необходимо решить дифференциальное уравнение:

Общее решение этого уравнения:

Предположим, что частное решение уравнения с правой частью есть

Мы специально задались полиномом не второй, а третьей степени. После выполнения операций дифференцирования , подстановки производных в исходное уравнение и упрощения уравнения получим:

Приравнивая коэффициенты, расположенные слева и справа от знака равенства с одинаковыми степенями , будем иметь:

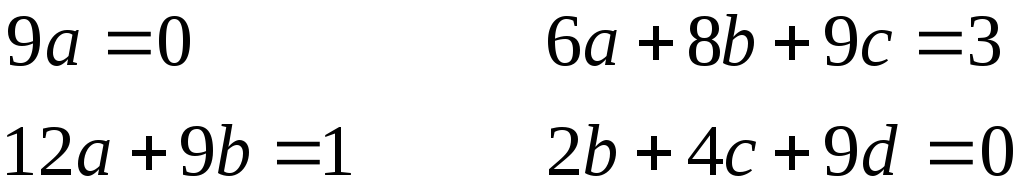
В окончательном виде: , то есть принужденная составляющая (частное решение)

Решение (сумма свободной и принужденной составляющих):

Тот факт, что , свидетельствует об отсутствии необходимости использования полинома третьей степени при выборе частного решения. Очевидно, в этом случае степени полиномов левой и правой частей уравнения должны быть равными.

2. Функция .

Частное решение необходимо выбирать с учетом того, каковы значения корней характеристического уравнения и .

Рассмотрим три возможных варианта выбора решения.

а) , то есть корни различные, и коэффициент не совпадает ни с одним из них.

Частное решение неоднородного уравнения выберем в виде

, (5.0)

где определяется через коэффициенты (5.3) и коэффициент :

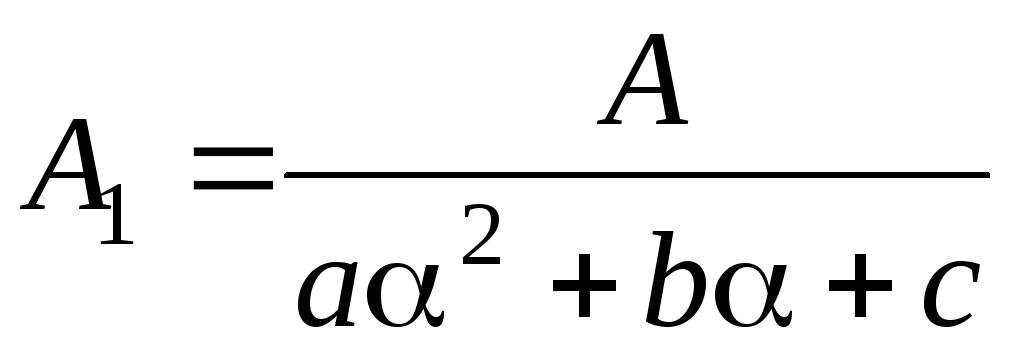
б) Корни действительные и различные, коэффициент равен одному из корней .

Функция равна:

, (5.0)

где .

в) Корни характеристического уравнения кратные, причем , . Тогда:

(5.0)

3. Рассмотрим случай, когда входной сигнал

, (5.0)

где , и – заданные постоянные значения.

а) Корни характеристического уравнения (5.4) действительные, либо комплексно-сопряженные: , причем при комплексно-сопряженных корнях, в свою очередь, либо , либо , . Тогда:

(5.0)

Искомые коэффициенты и определяются однозначно:

.

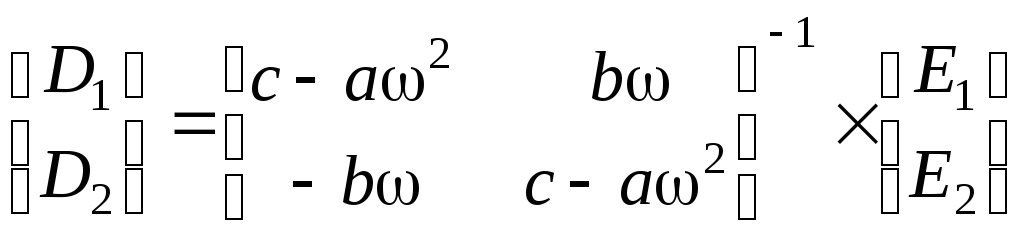б) корни характеристического уравнения (5.4) чисто мнимые: . В этом случае принужденная составляющая выбирается по формуле:

, (5.0)

где и получаются путем решения матричного уравнения

Если правая часть дифференциального уравнения (5.3) представляет собой аддитивную комбинацию рассмотренных выше функций, то каждому из слагаемых должна соответствовать своя часть , которая определяется одним из рассмотренных выше способов.

Пример. Получим решение дифференциального уравнения:

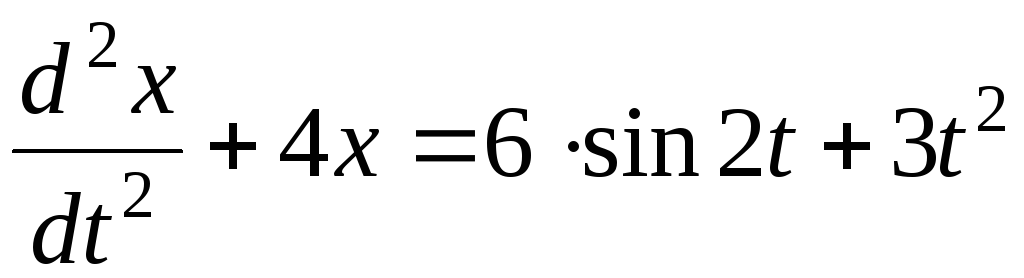
Решение. Характеристическое уравнение , поэтому корни . Следовательно, , . По формуле (5.7) при находим общее решение уравнения:

Можно предположить, что частное решение состоит из суммы двух решений.

Первое решение

,

согласно (5.14) и (5.15), соответствует слагаемому в правой части .

Второе решение вида

,

согласно (5.9) и (5.10), соответствует слагаемому в правой части . Однако при внимательном рассмотрении и мы видим, что здесь выполняется условие , причем содержится также во входном сигнале. Следовательно, для выбора мы должны использовать формулу (5.16)

.

Так как содержит члены, не встречающиеся в общем решении дифференциального уравнения, мы можем остановиться на первоначальном выборе . В окончательном виде частное решение (принужденная составляющая):

.

Подстановка в дифференциальное уравнение после взятия второй производной дает следующий результат:

.

Путем приравнивания коэффициентов с одинаковыми переменными частями слева и справа от знака равенства мы получим:

,

или окончательно:

.

Частное решение:

.

Решение дифференциального уравнения:

.

Постоянные коэффициенты и определяются из начальных условий и .

В заключение приведем алгоритм решения линейных дифференциальных уравнений с постоянными коэффициентами.

Для решения дифференциального уравнения необходимо:

1. Определить корни характеристического уравнения и записать общее решение дифференциального уравнения .

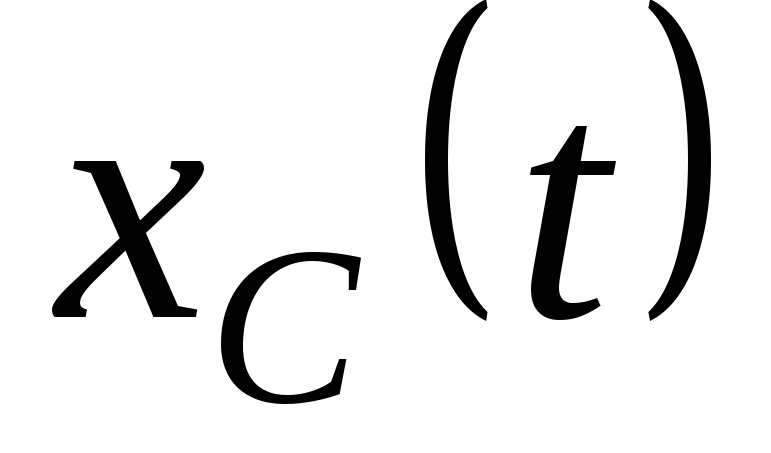2. Предположить, что частное решение соответствует членам, содержащимся в правой части дифференциального уравнения:

1. Для полинома 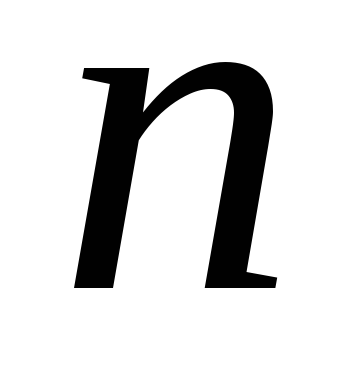-ой степени частным решением должен быть также полином -ой степени.

2. Для функций 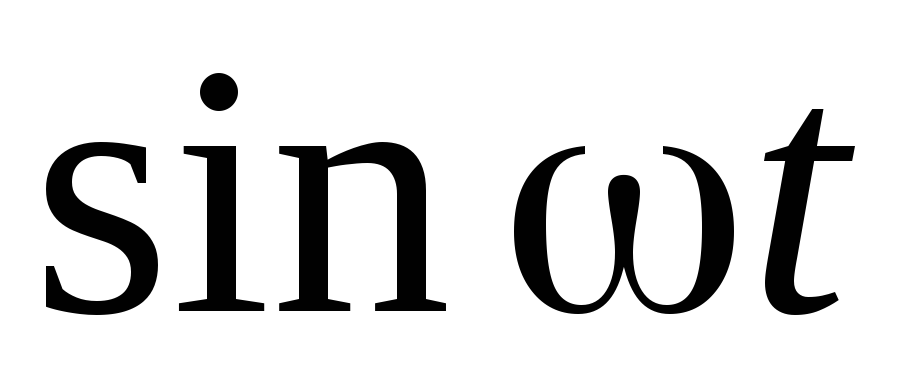, 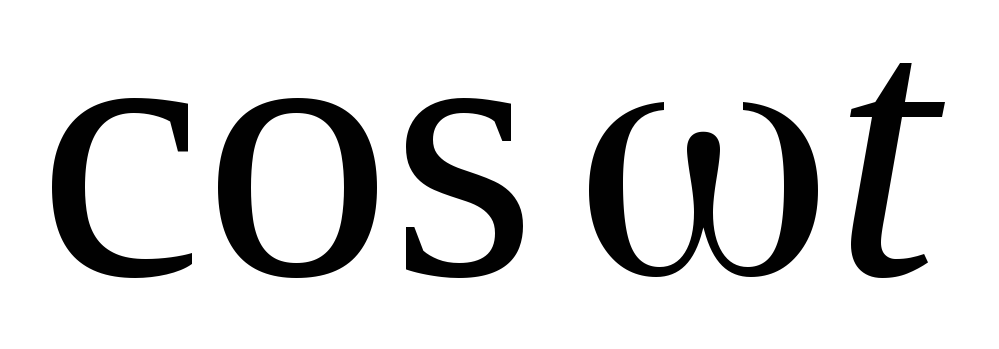или сумм и разностей таких функций в правой части, необходимо полагать, что частное решение .

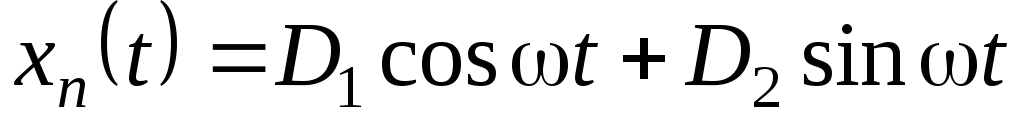3. Для функций вида 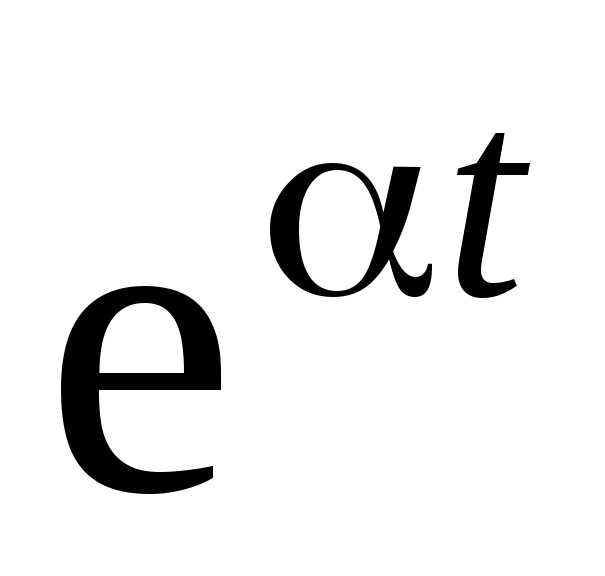следует полагать, что решение .

3. Если любое из предполагаемых решений, приведенных в пунктах 2(a, b или c), содержится также в общем решении дифференциального уравнения, мы должны умножить эти члены на время .

4. Записать предполагаемую форму частного решения и оценить коэффициенты, получив в результате .

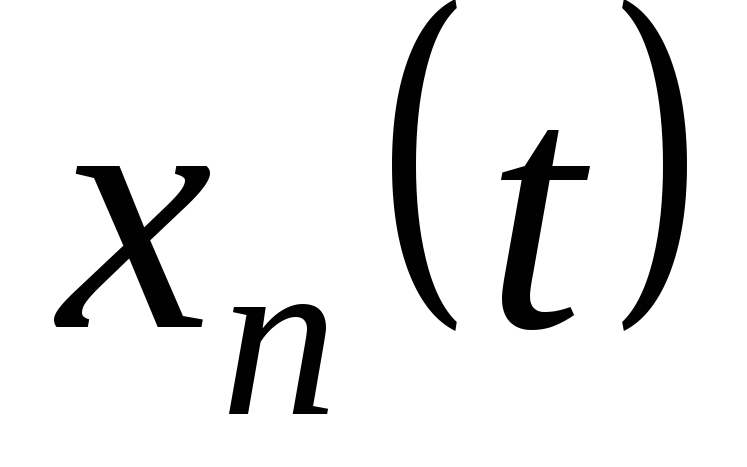5. Требуемое решение записать в виде суммы общего и частного решений: .

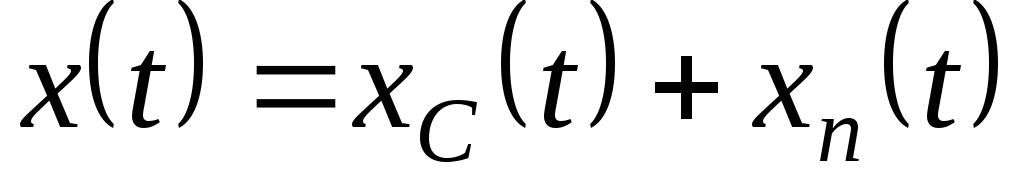6. Из начальных (граничных) условий определить постоянные интегрирования.