7. Модели детерминированного хаоса и их применение

7.1. Дискретные динамические модели первого порядка со сложной динамикой

Прежде всего, мы рассмотрим модели, описываемые разностными уравнениями первого порядка, с которыми приходится встречаться в биологических, экономических, технических и социальных системах. Несмотря на то, что уравнения имеют достаточно простой вид и описывают детерминированные процессы, в динамическом поведении моделей наблюдаются самые разнообразные режимы. Это обстоятельство требует сосредоточения особого внимания на выборе структуры и параметров моделей, адекватных поведению реальных объектов и систем [37].

Изучение динамических свойств дискретных моделей, представляемых разностным нелинейным уравнением первого порядка, обычно сводилось к определению условий устойчивости путем линеаризации при допущении условия, что модель подвергается малым возмущениям, приводящим к малым приращениям координат состояния. Однако дальнейшие исследования показали, что простейшие нелинейные разностные уравнения обладают широчайшим спектром поведения – от устойчивости точек, через каскад устойчивых циклов – к режиму детерминированного хаоса, а затем к стохастическому режиму [51].

Для эффективного использования моделей данного класса следует остановиться кратко на обзоре результатов исследований в этом направлении.

Мы остановимся на рассмотрении особенностей поведения нелинейной модели

, n=0,1,…. (7.1)

где f(.) – нелинейная функция. Предположим, что эта функция не аналитическая, т.е. она не может быть разложена в ряд.

В приложениях к моделям биологических популяций переменная состояния x имеет тенденцию роста на последующем шаге для малых значений на предыдущем, и тенденцию уменьшения – для больших x. В начале координат f(0)=0; функция монотонно возрастает в диапазоне 0<x<A ( f(x) достигает максимума в точке x=A); монотонное уменьшение происходит при значениях x>A. Функция может содержать один, либо несколько параметров, вариация которых оказывает существенное влияние на поведение (7.1). Иначе говоря, наблюдается высокая чувствительность модели к изменению параметров «настройки». Эти параметры, безусловно, имеют биологическую, экономическую, либо социологическую интерпретацию. Наиболее часто встречающиеся модели вида (7.1) содержат квадратичную нелинейность

, t=0,1,….. (7.2)

Это логистическое разностное уравнение. В пределе, когда b=0, с помощью (7.2) описывается чисто экспоненциальный рост популяции (для a>1). Для квадратичная нелинейность определяет функцию, обладающую свойством строгой выпуклости. Крутизна функции зависит от параметра . Вместо (7.2) часто используется ее каноническая форма, которая получается путем подстановки /a; t=n :

(7.3)

В дальнейшем мы будем также использовать запись (7.3), в которой a=4·r:

, (7.4)

поскольку в этом случае диапазон вариации r можно установить неравенство 0<r<1.Практические соображения, связанные с невозможностью получения отрицательных значений популяций на любом шаге, определяют ограничения диапазона изменения переменной состояния 0<x<1. В этой связи следует также отметить, что максимум f(x) соответствует x=0,5 и равен a/4. Уравнение (7.3) поэтому обладает нетривиальными свойствами, если а4. Кроме того, все траектории сходятся в точке х=0, если а1. Для уравнения (7.4) аналогичные свойства обеспечиваются при r1 и r.

В математической теории экологических процессов часто используется уравнение

. (7.5)

Оно также может быть отнесено к классу нелинейных систем (7.1). Модель (7.5) также описывает поведение популяции, соответствующее простому экспоненциальному росту при низких плотностях, и тенденцию к уменьшению численности популяции при высоких плотностях. Поведение модели весьма чувствительно к изменению параметра r. С помощью (7.5) принято описывать процессы роста популяций, вызывающих эпидемические болезни с высокими значениями плотности. Условия адекватности обеспечиваются, прежде всего, за счет экспоненциальной составляющей нелинейной функции.

Конечно, моделями (7.2) и (7.5) список динамических систем, простых в аналитическом описании, но сложных в поведении, ввиду большого разнообразия динамических свойств при неизменных структурах, вовсе не ограничивается [35] . В этой же работе, а также в работах [46], [47] можно найти большое число различных приложений, свидетельствующих (по названию последней работы) о важном научном направлении, связанном с изучением хаотических процессов и фракталей.

Остановимся кратко на анализе динамических свойств процессов, описываемых уравнением (7.1). Прежде всего отметим, что возможно определить равновесные значения (или «фиксированные точки») для переменной состояния Х, если положить в установившемся режиме X_n+1=X_n=X*. В этом случае (7.1) становится алгебраическим нелинейным уравнением

, (7.6)

что соответствует нулевому значению роста популяции. Для решения (7.6) можно использовать графические методы, отображающие X_n в состояние X_n+1 , которые представляются точками пересечения нелинейной функции с прямой, определяющей равенство X_n= X_n+1 (при одинаковых масштабах по осям абсцисс и ординат – это прямая в первом квадранте в декартовой системе координат под углом 45⁰ и проходящая через начало координат). Для простой строго выпуклой функции с одним максимумом, представляемой уравнениями (7.3) и (7.5), существуют две таких точки: тривиальное решение Х=0 и нетривиальное решение Х* (которое для модели (8.3) равно X*=1-).

Следующий вопрос, также связанный с устойчивостью модели в точке X*, состоит в оценке ее поведения, если тангенс угла наклона нелинейной характеристики в точке пересечения с вышеупомянутой прямой будет изменяться.

Наклон можно определить с помощью простого соотношения

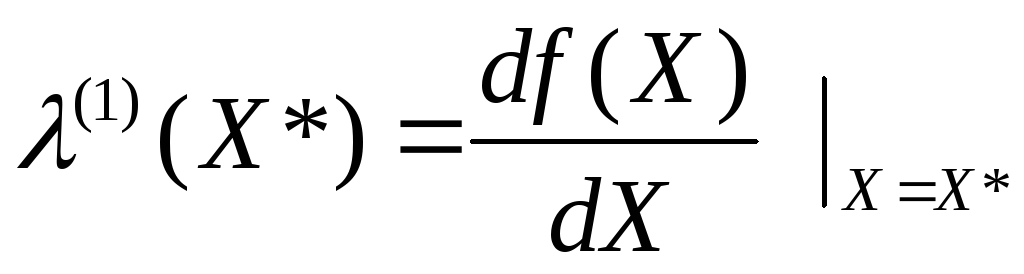(7.7)

Из (7.7) следует, что если наклон поддерживается в диапазоне от 45⁰ до -45⁰ (т.е. значения изменяются на интервале от 1 до -1), точка равновесия X* будет устойчивой. Она будет обладать свойством притяжения, т.е. являться аттрактором для любой из наблюдаемых траекторий. В частности, модель (7.3) с наклоном будет обладать свойством притяжения всех траекторий к точке в начале координат в интервале x1, если и только если 1а3. За пределами этого интервала параметр а определяет совершенно иные свойства модели.

Заметим, что координата состояния на (n+2)-ом интервале, согласно (7.1), равна

(7.8)

Используя вместо (7.8) выражение, соответствующее установившемуся режиму, мы получим алгебраическое уравнение

(7.9)

Пересечение кривой с прямой линией теперь будет происходить в двух точках, т.е. будет порождаться двухпериодический процесс. Если наклон характеристики (7.9), определяемый по уравнению (7.7),

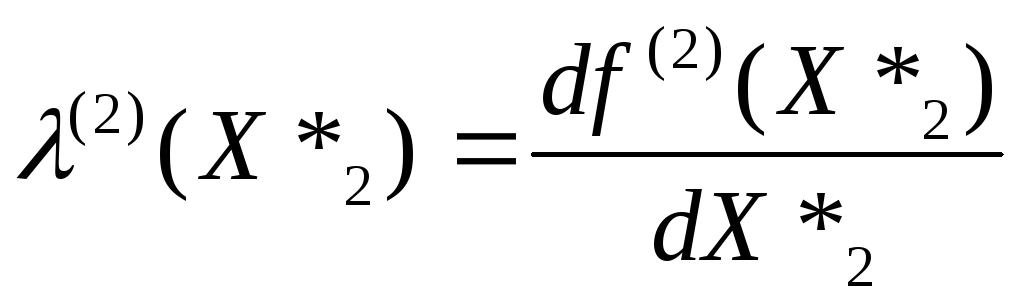(7.10)

находится в интервале л⁽²⁾, что соответствует углу наклона от 0⁰ до 45⁰, будет наблюдаться устойчивый режим при нетривиальном решении (7.9). Если же углы наклона нелинейной характеристики в точке пересечения с прямой будут таковы, что по абсолютному значению |л⁽²⁾|, в системе (7.9) установятся двухпериодические колебания. Базовая точка при этом, соответствующая режиму л⁽¹⁾, является неустойчивой. В частности, двухпериодический цикл можно наблюдать в системе (7.3), если а=3.414. Тогда кривая пересекает прямую (т.е. получается решение (7.9)) в трех точках. Между точками, соответствующими устойчивому двухпериодическому процессу, лежит базисная фиксированная точка, в которой процесс неустойчив.

Дальнейшее увеличение параметра а порождает неустойчивость двухпериодического процесса и устойчивый четырехпереодический цикл, а затем порождает также устойчивые циклы с периодами 8,16,32,64,…,2ⁿ. Иначе говоря, каждый предшествующий процесс с периодом к с увеличением а становится неустойчивым, одновременно бифурцирует, в результате возникает устойчивый цикл периода 2к. Наконец, возникает режим детерминированного хаоса, который далее (при значениях а, близких к 4) будет иметь настолько «узкие» границы («окна») сохранения устойчивого t-периодического процесса, что они могут быть сравнимы с погрешностью «машинного нуля». В этом случае хаотический процесс практически становится стохастическим.

В хаотическом режиме модель обладает рядом интересных свойств. Например, при незначительном изменении начальных условий траектории процессов могут с течением времени сильно расходиться. Следовательно, даже по простой модели с точно определенными коэффициентами невозможно предсказать длительное поведение с малой погрешностью. Этот феномен, исследуя метеорологические процессы, Лоренц назвал «эффектом бабочки». Он утверждал, что если даже атмосферные явления удалось бы описать с помощью детерминированной системы уравнений со всеми известными параметрами, колебания крыльев бабочки порождали бы начальные условия, которые в хаотическом режиме не позволили бы точно предсказать процессы на большом временном интервале. При изменении же коэффициентов и начальных условий процессы становятся практически стохастическими.

Классическим примером хаотических систем в гидромеханике являются турбулентные течения и влияние на них изменения параметра – числа Рейнольдса [4]. Система детерминированных уравнений Навье-Стокса, описывающих движения жидкости, при изменении параметра (числа Рейнольдса) позволяет получить резкие переходы из одного состояния в другое (например, переход от ламинарного течения к турбулентному и наоборот) [7]. Кроме традиционных уравнений Навье-Стокса, в работах Белоцерковского О.М. отмечается возможность использования моделей класса (7.1) для описания динамики турбулентности течений, что обеспечивается богатым спектром динамического поведения моделей и возможностью использования процедур пригонки их параметров к экспериментальным данным.