4. Модели пространства состояний в электрических цепях и системах

Для моделирования электрических цепей и динамических систем естественно использовать переменные состояния как обобщающие характеристики. Метод пространства состояний, базирующийся на приме­нении матричного анализа, позволяет использовать фундаментальные по­ложения высшей алгебры для эффективного решения прикладных задач. Основные преимущества метода пространства состояний реально прояв­ляются уже на начальной стадии расчета - при составлении дифференци­альных уравнений, описывающих переходные процессы в динамических системах с сосредоточенными параметрами [16].

Рассматривая физические процессы, которые могут быть адекватно описаны системами алгебраических или обыкновенных дифференциаль­ных уравнений в матричной форме, мы остановимся на анализе динамики электрических цепей и простых динамических систем.

Наряду с возможностями получения решения уравнений состояния в аналитическом виде, мы рассмотрим технические приемы составления уравнений, их преобразования, а также машинные методы качественного и количественного анализа динамики моделей и систем.

4.1. Понятие состояния

Предположим, что состояние системы может быть описано n-мерным вектором:

(4.1)

содержащим п компонент, являющихся функциями времени t. Про­странством состояний системы является пространство, в котором ба­зисный вектор может быть выбран из множества векторов

Если моделируемая система допускает аналитическое описание про­цессов в терминах пространства состояний с помощью обыкновенных дифференциальных уравнений, то уравнения состояния можно привести к стандартной форме:

(4.2)

(4.3)

где - вектор управления размерности (rl); - вектор выхода размерности (m1), причем т  п. В общем, нелинейные вектор - функции и , имеющие соответствующие размерности, являются однозначными.

Можно полагать, что состояние системы, как понятие, содержит всю информацию о поведении системы в прошлом и позволяет оценить это по­ведение в будущем как реакцию на заданный входной сигнал. Так, если со­стояние системы описывается линейными дифференциальными уравне­ниями с постоянными коэффициентами, то решение может быть определе­но состоянием в начальный момент t₀, т.е. вектором .

Способы записи уравнений состояния различны, для различных фи­зических систем и определяются удобствами анализа систем в конкретных условиях.

Математическая модель состояния стационарной линейной системы представляется матричным дифференциальным уравнением вида [2]:

(4.4)

(4.5)

где А, В, С и D - матрицы соответствующих размерностей, элементы которых являются постоянными коэффициентами.

Интегрирование (4.4) при начальных условиях позволяет полу­чить:

(4.6)

Рассмотрим составление уравнений на примере динамической сис­темы второго порядка.

Из курса физики известно, что если тело массой т движется в среде с сопротивлением и сопротивление, действующее на тело, пропорциональ­но скорости движения (демпфирующая сила), то уравнение движения та­кой неконсервативной системы:

(4.7)

где х - смещение тела, К и С_х - постоянные коэффициенты, F(t) - сила, воздействующая на тело от внешнего источника.

Уравнение (4.7) можно записать в терминах пространства состояний.

Введем вектор и обозначим .

Тогда динамическую систему (4.7) можно представить в виде двух дифференциальных уравнений первого порядка:

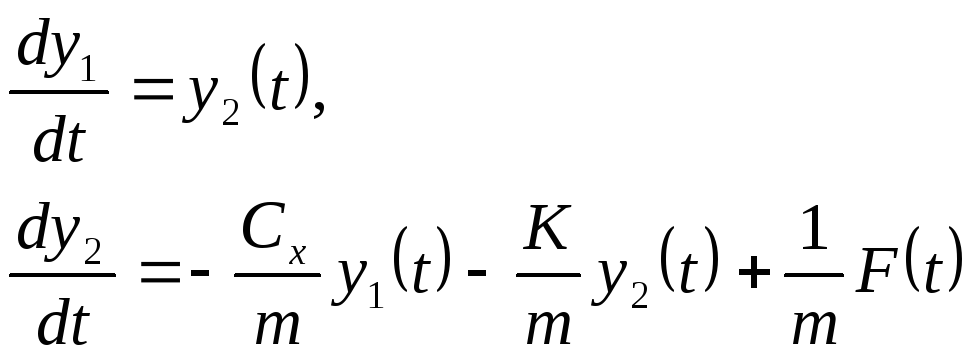
которые нетрудно записать в матричной форме, используя введенный вектор состояния.

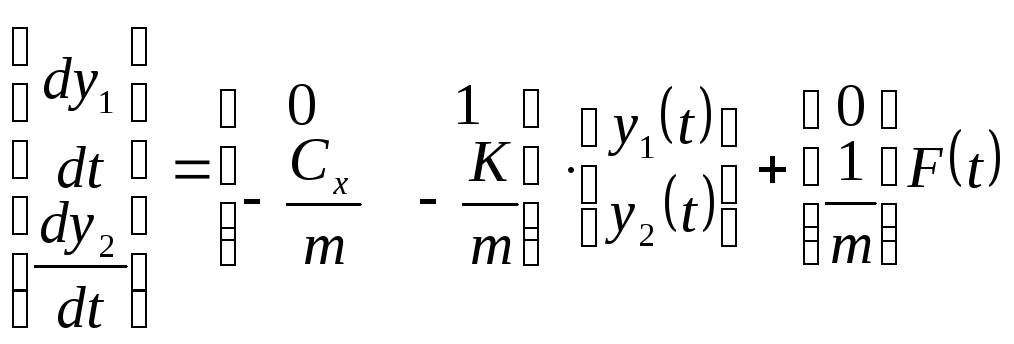(4.8)

Сопоставив уравнение (4.8) с математической моделью состояния (4.4), мы можем убедиться, что (4.8) является стационарной системой.

Метод пространства состояний обеспечивает упорядоченный подход к нахождению состояния системы как функции времени, базирующийся на решении дифференциальных уравнений в матричной форме.

Под перемен­ными состояния обычно понимают величины, определяющие энергетиче­ское состояние системы. Их значения полагают известными к началу про­цесса