1.6. Нормы оценивания параметров в теории инверсных систем

Остановимся кратко на анализе центральных оценивателей и оценивателей дисперсии, используемых в теории инверсных систем.

Одномерный процесс.

Предположим, что задана нормализованная одномерная функция плотности распределения вероятности f(x). Рассмотрим выражение

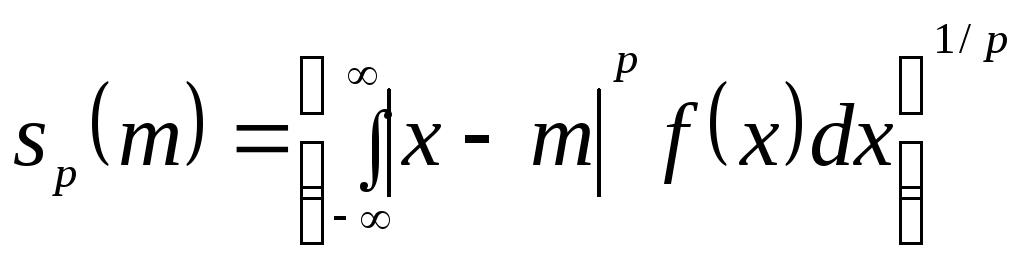(1.47)

Для заданного p выберем значение т, которое доставляет минимум s_p(m). Обозначим его в виде т_р. Очевидно, т_р можно назвать центром f(x) в смысле l_р-нормы (1.47). Значение m₁ есть медиана, m₂ — среднее (или математическое ожидание), m_ - срединный размах (l_ - норма).

Медиана соответствует минимуму l₁ нормы

- минимум 

среднее значение соответствует минимуму l₂ -нормы:

- минимум 

при минимуме l_р - нормы можно оценить т_:

для

Значение функциив стационарных точках минимума опреде­ляет дисперсию в критериальном смысле l_р -нормы и обозначается _p:

(1.48)

Очевидно, ₁ - среднее отклонение, ₂- стандартное отклонение, _ - половина диапазона. При этом учитываются следующие свойства:

среднее отклонение (минимум l₁ - нормы):

стандартное отклонение (минимум l₂-нормы):

полуразмах (минимум l_ -нормы):

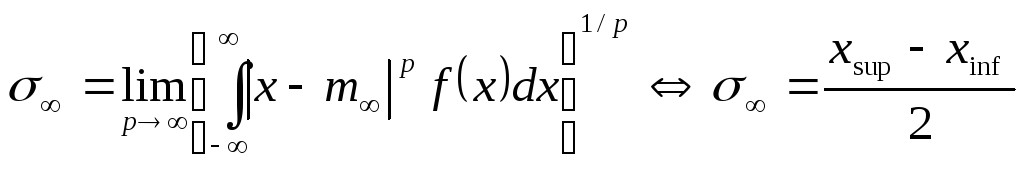
Многомерный процесс.

В этом случае задается функция плотности вероятности f(x), опре­деляемая для вектора переменных x ={xⁱ} ; . Рассматривается опера­тор с₂(m), определяемый с помощью элементов вектора x:

(1.49)

Вектор m₂, минимизирующий диагональные элементы оператора с₂ (m), определяется как среднее (или математическое ожидание) вектора x в смысле l₂ -нормы. Он вычисляется с помощью интеграла

Если m = m₂, то оператор (1.49) представляет собой ковариацию вектора x в смысле l₂-нормы, которую можно обозначить в виде C₂:

(1.50)

Заметим, что диагональные элементы C₂ равны дисперсиям (квадра­там стандартных отклонений), которые ранее обозначались как :

Свойства ковариации (при норме l₂) приведены в классической ра­боте Пугачева B.C.:

a) свойство симметрии -

b) C₂ является неотрицательно определенной - для любого вектора x

c) если C₂ положительно определена, то для любого вектора x величина имеет свойства нормы. Она определяется как весо­вая l₂ -норма вектора x;

d) корреляционные коэффициенты определяемые по формуле , обладают следующим важным свойством - ;

e) плотность вероятности

где N - размерность вектора x, нормализуется со средним значением х₀ и ковариационным оператором с₂ [39].

Среди всех плотностей вероятностей с заданной нормой l₂ оператора ковариации, функция Гаусса соответствует минимуму информации (т.е. функция имеет максимум при минимуме показателя степени экспоненты).

Остановимся теперь на обобщении процесса с нормальным распре­делением. Среди всех нормированных плотностей вероятности по норме l_р оцениватель дисперсии

единственный удовлетворяет условию минимума информации. Эта плот­ность представляется уравнением

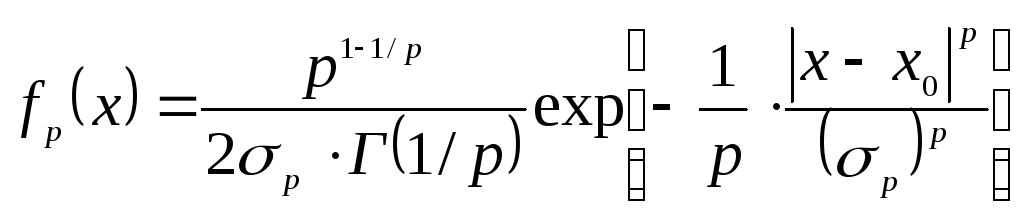(1.51)

где Г() есть гамма-функция [42].

Задаваясь различными значениями p, можно построить обобщенную характеристику, изменяющую форму в зависимости от нормы. B частности, если p = 1

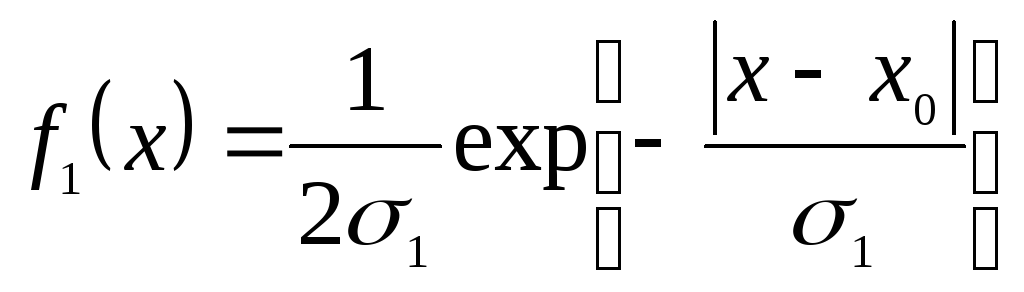
и - симметричная экспонента, центрированная при со сред­ним отклонением ₁. Для р = 2

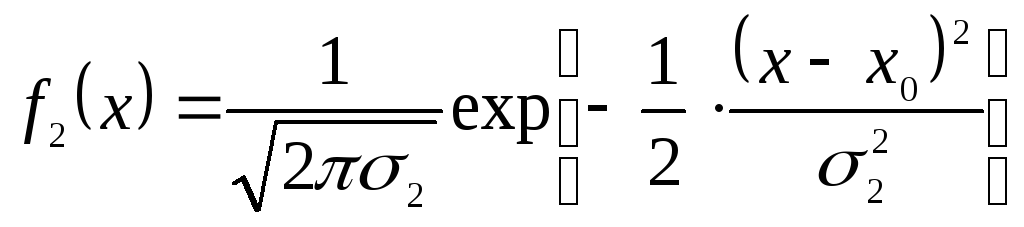
есть функция Гаусса со стандартным отклонением ₂. Для p = 

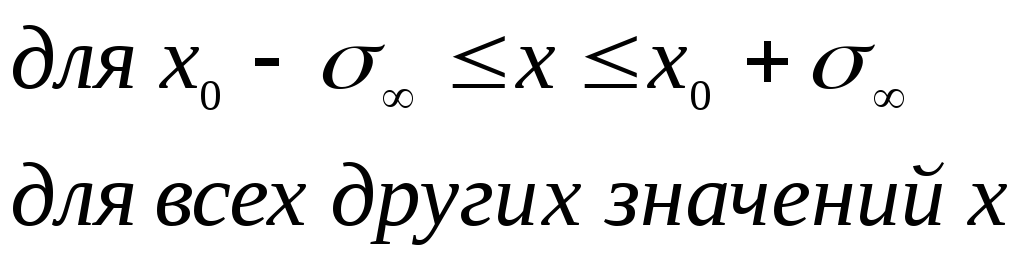
Функция имеет прямоугольную форму, центрированную при с размахом, равным _. Функция нормирована к единице.

Функцию (1.51) называют также обобщенным гауссианом, т.к. она генерирует семейство функций, содержащих в своем составе функцию Га­усса. Отметим, что приведенные выше функции часто используются для моделирования распределений ошибок. Введение обобщенного гауссиана способствует некоторому расширению возможности выбора распределе­ний для оценки погрешностей сигналов в измерительных средствах судо­вых энергетических комплексов.

Большое практическое применение получили оцениватели по норме p= 1. Для такой оценки мы предлагаем эффективный алгоритм, основанный на выборе минимальных составляющих вектора погрешностей, получен­ных на начальной стадии решения с помощью изложенного выше метода наименьших квадратов.

Если в критерии (1.47) предположить симметрию относительно т_р и перейти от интеграла к дискретным оценкам, приняв за основу уравнение измерителя в форме (1.49), то критерий каче­ства примет следующий вид:

(1.52)

где p  1. Если р = 2, то J₂ (х) естъ корень квадратный из суммы квадратов остатков, так что минимизация J₂ (x) эквивалентна наилучшей оценке по методу наименьших квадратов.

Статистические свойства средней амплитудной и среднеквадратической оценок можно интерпретировать следующим образом. Среднеквадратическая оценка соответствует определению среднего квадрата множества измерений, в то время как оценка по критерию L₁ - нахождению среднего значения множества измерений. Использование среднего значения в про­цедуре оценивания состоит в нахождении n (число переменных состояния) остатков, равных нулю, и (m – n) ненулевых остатков (т — число измере­ний). При этом предполагается, что, в общем, каждое измерение может подвергаться воздействию шума Гаусса. Использование весовых факторов изменяет дисперсию шума измерений, так что в целом система измерений может рассматриваться как имеющая шумовую составляющую, представ­ляемую распределением Гаусса со смешанной дисперсией. Для распреде­лений Гаусса со смешанными дисперсиями, а также для негауссовских распределений среднее амплитудное оценивание дает хорошие практиче­ские результаты. Это утверждение основывается на целом ряде работ, где проблема минимизации линейного критерия качества решалась с помощью симплекс-метода, являющегося основным методом поиска оптимума в ли­нейном программировании [19].