Символьной алгебры

Необходимо определить токи в ветвях, если сопротивления равны:

, , , , , , и ЭДС источников , , , , . (сопротивления – в Омах, ЭДС – в Вольтах). К первому узлу подтекает ток , а от второго – оттекает .

Обозначим потенциалы узлов 1, 2 и 3: , , . Потенциал узла 4 принят равным нулю (см. рис. 6.2). Воспользуемся методом узловых потенциалов и составим уравнения:

,

, (6.2)

,

где - собственные проводимости узлов,

- взаимные проводимости.

Определим численные значения собственных и взаимных проводимостей, входящих в систему (6.2):

, , .

Вычислим токи узлов, согласно методу узловых потенциалов:

,

,

.

Система уравнений (6.2) принимает вид:

,

,

.

Найдем потенциалы узлов с помощью символьного метода. Объявим , и символьными переменными и, используя функцию solve, решим систему уравнений :

syms u1 u2 u3

f1='1.25*u1-0.05*u2-0.2*u3=68';

f2='-0.05*u1+0.45*u2-0.1*u3=5';

f3='-0.2*u1-0.1*u2+0.8*u3=-35';

[u1 u2 u3]=solve(f1,f2,f3);

В результате получим: , , .

Токи в ветвях рассчитаем с помощью уравнений:

; ;

; ;

; ;

.

Для выполнения расчетов был использован файл sah383.m.

% sah383.m

% DC- electrical system design:

syms u1 u2 u3

f1='1.25*u1-0.05*u2-0.2*u3=68';

f2='-0.05*u1+0.45*u2-0.1*u3=5';

f3='-0.2*u1-0.1*u2+0.8*u3=-35';

[u1 u2 u3]=solve(f1,f2,f3);

[u1 u2 u3]

%==============================

I1=(u1-u2+200)/20;

I2=(u3-u1+80)/5;

I3=(u2-u3)/10;

I4=(u2+30)/10;

I5=u2/5;

I6=(u3+38)/2;

I7=(-u1+60)/1;

I=[I1 I2 I3 I4 I5 I6 I7]'

В первом блоке файла объявлены символьные напряжения узлов электрической цепи (рис. 6.2), записаны уравнения и , согласно рассмотренному выше синтаксису функции solve.

Полученные расчетные значения , и во втором блоке использованы в уравнениях токов ветвей. Положительные направления токов в ветвях, в которых содержатся источники ЭДС, приняты совпадающими с направлениями ЭДС (рис. 6.2).

6.3. Символьное дифференцирование и интегрирование

Непрерывная функция f(x), имеющая дифференциал в каждой точке , называется дифференцируемой. Разрывная функция в точке разрыва не имеет дифференциала.

Для получения производных от функций по аргументу в символьном виде используется diff, записываемая в формате diff(f), diff(f, ‘y’) или diff(f, k), где k – целое число. Первые две формы возвращают значение первой производной от символьного выражения. С помощью символа ‘y’, указанного в круглых скобках, выполняется взятие производной по переменной ‘y’. В последней форме с помощью k определяется порядок производной от функции f.

В приведенных ниже примерах вычисления производных, кроме функции diff, использовалась функция упрощения выражения simplify, а также функция pretty, позволяющая выводить результаты преобразований в естественной математической форме, с использованием общепринятых математических знаков для записи математических выражений. В них используются, в частности, надстрочные показатели степени, знаки деления в виде горизонтальной черты и т.п. Нетрудно видеть, что переход от производной к записи дифференциала функции может быть осуществлен добавлением соответствующих знаков дифференциала, с учетом свойств. Во всех примерах сохранены машинные данные вычислений, за исключением примера 2, где представлен результат в виде дифференциала сложной функции, а также примера 5, в котором выполнено дифференцирование произведения двух функций. В примере 10 определена третья производная от степенной функции (k=3).

1. Степенная функция

syms x y m n

z1=diff(x^m);

z=simplify(z1)

pretty(z)

z =

x^(m-1)*m

(m - 1)

x m

2. Дифференцирование сложной функции

f=(1+x^2)^3;

f1=diff(f);

f2=simplify(f1)

pretty(f2)

d(f2) =

6*(1+x^2)^2*x*dx

2 2

6 (1 + x ) x dx

3. Производная сложной функции

fa=sqrt(n^2-x^2);

fa1=diff(fa);

fa2=simplify(fa1)

pretty(fa2)

fa2 =

-1/(n^2-x^2)^(1/2)*x

x

- ------------

2 2 1/2

(n - x )

4. Производная гармонической функции

fb=sin(2*x)^2;

fb1=diff(fb);

fb2=simplify(fb1)

pretty(fb2)

fb2 =

4*sin(2*x)*cos(2*x)

4 sin(2 x) cos(2 x)

5. Дифференцирование произведения двух функций

fc=(2*x^2+3*x)*(x^3-2);

fc1=diff(fc);

fc2=simplify(fc1)

pretty(fc2)

d(fc2) =

(10*x^4-8*x+12*x^3-6)*dx

4 3

(10 x - 8 x + 12 x - 6) dx

6. Производная от частного (дроби)

fd=sqrt((1+x)/(1-x));

fd1=diff(fd);

fd2=simplify(fd1)

pretty(fd2)

fd2 =

1/(-(1+x)/(x-1))^(1/2)/(x-1)^2

1

---------------------

/ 1 + x\1/2 2

|- -----| (x - 1)

\ x - 1/

7. Производная от логарифмической функции

fe=x*exp(-x^2);

fe1=diff(fe);

fe2=simplify(fe1)

pretty(fe2)

fe2 =

exp(-x^2)-2*x^2*exp(-x^2)

2 2 2

exp(-x ) - 2 x exp(-x )

8. Производная от тригонометрической функции

fg=log(sqrt(sin(2*x)));

fg1=diff(fg);

fg2=simplify(fg1)

pretty(fg2)

fg2 =

1/sin(2*x)*cos(2*x)

cos(2 x)

--------

sin(2 x)

9. Частные производные от функции

fh=log(sqrt(x^2+y^2));

fh1=diff(fh);

fh2=diff(fh,y);

fh3=simplify(fh1)

fh4=simplify(fh2)

pretty(fh3)

pretty(fh4)

fh3 =

1/(x^2+y^2)*x

fh4 =

1/(x^2+y^2)*y

x

-------

2 2

x + y

y

-------

2 2

x + y

10. Третья производная от степенной функции

fm=x^4;

fm1=diff(fm,3);

fm2=simplify(fm1)

pretty(fm2)

fm2 =

24*x

24 x

В процессе проведения инженерных расчетов часто возникает необходимость вычисления интегралов. Для интегрирования символьных аналитических зависимостей предназначена функция int. Если интеграл в замкнутой форме не существует, либо MatLAB не может по каким-либо иным причинам выполнить вычисления, то на дисплее об этом появляется сообщение.

Подобно функции diff, существует также несколько способов использования int. Рассмотрим вычисление неопределенного интеграла подынтегральной функции f(x) с переменной интегрирования х. Попытаемся получить некоторые соотношения, часть которых при изучении интегрального исчисления рекомендовалось знать на память.

Пример 1

f=x^n;

f1=int(f)

pretty(f1)

f1 =

x^(n+1)/(n+1)

(n + 1)

x

--------

n + 1

Пример 2

fa=1/x;

fa1=int(fa)

pretty(fa1)

fa1 =

log(x)

log(x)

Пример 3

fb=exp(x);

fb1=int(fb)

pretty(fb1)

fb1 =

exp(x)

exp(x)

Пример 4

fc=a^x;

fc1=int(fc)

pretty(fc1)

fc1 =

1/log(a)*a^x

x

a

------

log(a)

Пример 5

fd=sin(x);

fd1=int(sin(x))

pretty(fd1)

fd1 =

-cos(x)

-cos(x)

Пример 6

fe=cos(x);

fe1=int(fe)

pretty(fe1)

fe1 =

sin(x)

sin(x)

Пример 7

ff=1/(sin(x)^2);

ff1=int(ff)

pretty(ff1)

ff1 =

-1/sin(x)*cos(x)

cos(x)

- ------

sin(x)

Пример 8

fk=1/(cos(x)^2);

fk1=int(fk)

pretty(fk1)

fk1 =

1/cos(x)*sin(x)

sin(x)

------

cos(x)

Пример 9

fg=1/sqrt(1-x^2);

fg1=int(fg)

pretty(fg1)

fg1 =

asin(x)

asin(x)

Пример 10

fh=1/sqrt(a^2-x^2);

fh1=int(fh)

fh2=simplify(fh1)

pretty(fh2)

fh3=simplify(diff(fh2))

fh1 =

atan(x/(a^2-x^2)^(1/2))

fh2 =

atan(x/(a^2-x^2)^(1/2))

x

atan(------------)

2 2 1/2

(a - x )

fh3 =

1/(a^2-x^2)^(1/2)

Пример 11

fm=1/(a^2+x^2);

fm1=int(fm)

pretty(fm1)

fm1 =

1/a*atan(x/a)

atan(x/a)

---------

a

Пример 12

fn=1/sqrt(x^2-a^2);

fn1=int(fn)

pretty(fn1)

fn1 =

log(x+(-a^2+x^2)^(1/2))

2 2 1/2

log(x + (-a + x ) )

Обратим внимание на то, что полученные неопределенные интегралы во всех примерах не содержат постоянной интегрирования «С», которая должна быть добавлена к каждому решению.

Поскольку интеграл функции является первообразной для самой функции, путем операции дифференцирования мы можем получить каждую исходную функцию. В примере 10 для этой цели использована запись:

.

В результате

,

что свидетельствует о корректности вычислений .

Другая форма записи int(f, y) возвращает неопределенный интеграл по переменной y.

Наконец, остановимся на определенном интеграле. Недостающие значения параметров, задающие интервал интегрирования [a, b], записываются следующим образом:

int(f, a, b), либо int(f, y, a, b).

Если, например, требуется найти интеграл функции

в пределах [1, 4], необходимо использовать такую форму записи:

В результате получим:

Граничные значения могут быть заданы символами [a, b]:

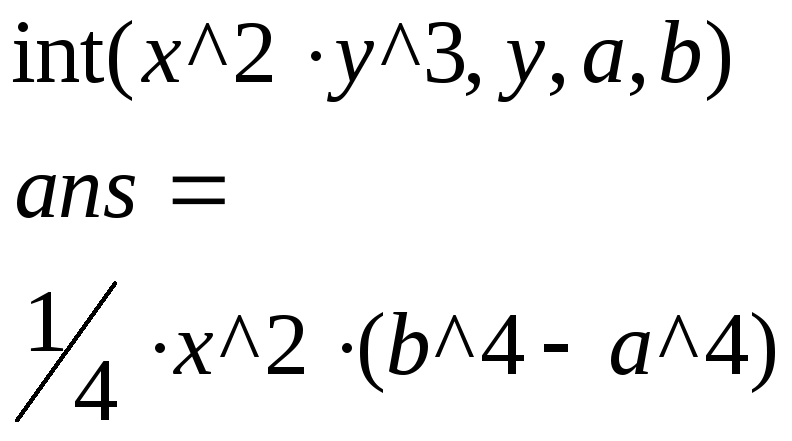
В известных случаях, когда границы интегрирования заданы таким образом, что подынтегральное выражение содержит условие вырожденности, определенный интеграл не должен вычисляться. Однако неопределенный интеграл этой же функции может быть найден. Приведем пример:

.

Но вычисление определенного интеграла

не производится, поскольку при х=2 знаменатель равен нулю. Вместе с тем с изменением верхней границы интегрирования, исключающим сингулярность, решение может быть получено:

.

Операции интегрирования и дифференцирования часто используются при выполнении расчетов установившихся и переходных процессов в электрических цепях. Символьные функции могут эффективно применяться для выполнения таких расчетов, а в случае необходимости – для проверки корректности выполняемых преобразований и получения справочных данных.

Остановимся на рассмотрении двух примеров.

В первом примере вычислим среднее и действующее значения синусоидально изменяющегося тока. Напомним, что под средним значением синусоидально изменяющейся величины понимают ее среднее значение за половину периода. Следовательно, если ток в цепи изменяется по синусоидальному закону

,

где - угловая частота, Т- период (время, за которое совершается одно полное колебание), - амплитуда тока, - время, то среднее значение синусоидального тока можно вычислить путем интегрирования функции:

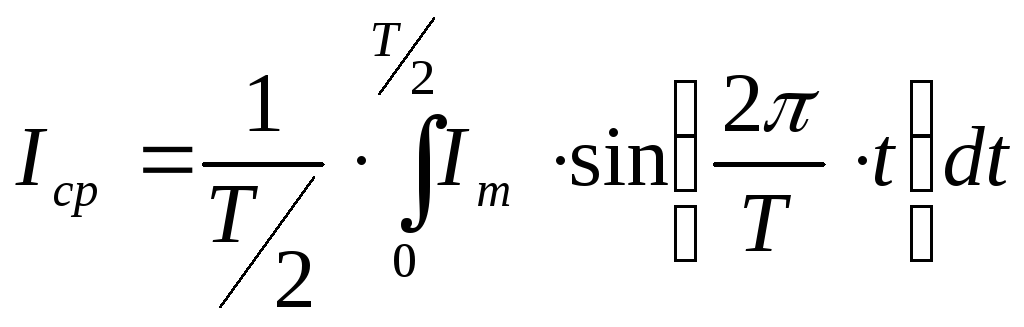(6.3)

Действующее значение синусоидального тока

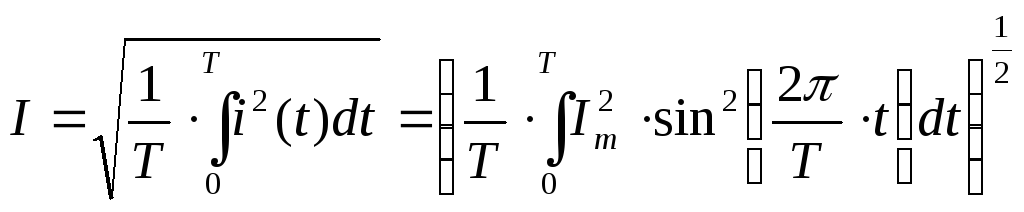(6.4)

является среднеквадратичной величиной. Ток численно равен значению такого постоянного тока, который за время одного периода синусоидального тока выделяет на активном сопротивлении такое же количество теплоты, что и синусоидальный ток .

Определим в символьных выражениях и , для чего (6.3) и (6.4) запишем следующим образом:

% Mean and meansquare current:

syms Im T t

Icp=1/(T/2)*int(Im*sin(2*pi/T*t),t,0,T/2);

pretty(Icp)

I=sqrt(1/T*int(Im^2*sin(2*pi/T*t)^2,t,0,T));

pretty(I)

Im

2 ----

pi

1/2 2 1/2

1/2 2 (Im ) = Im/ 2^1/2

Возвращенные значения токов позволяют определить и в терминах :

.

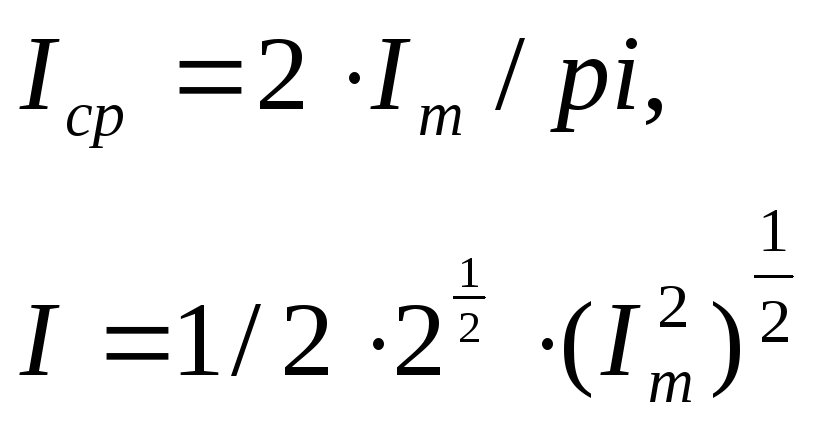Таким образом, получены известные состояния:

Второй пример будет содержать процедуру определения напряжения на индуктивности по известному току и параметру с помощью функции дифференцирования. Рассмотрим неразветвленную электрическую цепь, состоящую из последовательно соединенных резисторов R, R0 и индуктивности L. Цепь подключена к источнику постоянной ЭДС, равной E. В момент t=0 резистор R0 шунтируется ключом, и в цепи будет наблюдаться переходный процесс при ненулевых начальных условиях. Основная переменная состояния – ток через индуктивность. Для основной переменной состояния (тока через индуктивность) запишем уравнение:

.

Это уравнение можно использовать для расчета в символьной форме напряжения на индуктивности по формуле:

,

для чего требуется объявить символьные величины, а затем с помощью функции diff, как показано ниже, найти искомое соотношение. В синтаксисе функции diff, конечно, следует указать аргумент , по которому производится дифференцирование:

% Уравнение для i_L(t) :

syms E R L R0 t

i=E/R*(1-exp(-R/L*t))+E/(R+R0)*exp(-R/L*t);

u=L*diff(i,t)

simplify(u)

u =

L*(E/L*exp(-R/L*t)-E/(R+R0)*R/L*exp(-R/L*t))

ans =

E*exp(-R/L*t)*R0/(R+R0)

Таким образом, напряжение на индуктивности в момент принимает максимальное значение (изменяется скачком)

а по окончании переходного процесса

,

при становится равным нулю. Из приведенного символьного текста видно, что после операции дифференцирования использована функция simplify для поэлементного упрощения символьного выражения .