6.5. Моделирование переходных процессов в электрических цепях средствами пакета символьной математики

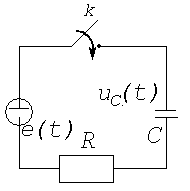
На рис. 6.3 изображена RC-цепь, которая подключается к источнику с изменяющейся во времени ЭДС Переходный процесс в цепи с момента замыкания ключа «К» описывается дифференциальным уравнением

, (6.5)

где - постоянная времени.

Рис.6.3. RC- цепь с произвольно изменяющейся ЭДС

Положим сначала при сохранении внутреннего сопротивления источника ЭДС. Если , то в цепи будет наблюдаться переходный процесс только при наличии заряда конденсатора в момент . Тогда , и по завершении переходного процесса на активном сопротивлении в виде тепла будет полностью рассеяна энергия

,

и ток разряда при нулевом напряжении на емкости.

В переходном режиме не может изменяться скачком. Согласно второму закону Кирхгофа, переходный процесс в цепи (рис. 6.3) описывается дифференциальным уравнением

, .

Его решение в аналитическом виде получим с помощью функции dsolve, для чего сначала введем символьные объекты. Затем определим ток путем дифференцирования и последующего умножения на постоянный коэффициент (величину емкости). В символьной записи решение имеет вид:

>> syms R C Uc t

Uc=dsolve('DUc=-1/(R.C)*Uc')

i=C*diff(Uc)

Uc =

C1*exp(-1/RC*t)

i =

-C*C1/RC*exp(-1/RC*t)

>>

В приведенных формулах - постоянная интегрирования, определяемая с учетом начальных условий. Ток с отрицательным знаком, что свидетельствует о разряде конденсатора.

Чтобы получить численные результаты и использовать символьную форму уравнений для графических построений, выберем следующие значения параметров электрической цепи:

Ом, мкФ, В, с.

Решение получено с помощью следующих операций:

>> RC=0.1;C=100e-06;R=1000;

Uc1=dsolve('DUc=-1/(0.1)*Uc','Uc(0)=7')

i1=C*diff(Uc1)

tt=0:0.0011:0.45;

Vc=subs(Uc1,'t',tt);

I=subs(i1,'t',tt);

p=R*I.^2;

plot(tt,Vc,tt,I*1e03,tt,p*1e02),grid

xlabel('Time, sec'),ylabel('Vc(t),I(t),p(t)')

Uc1 =

7*exp(-10*t)

i1 =

-7/1000*exp(-10*t)

>>

Здесь дважды использована функция подстановки subs для вычисления и . Вектор с шагом 0.0011с подставляется вместо аргумента в выражениях:

и .

Затем рассчитываются текущие значения мощности и выполняются графические построения (рис. 6.4).

Если учесть, что

,

где - постоянная времени, то для мощности получим:

.

Следовательно, и скорость уменьшения в функции времени в момент в два раза выше скорости уменьшения и , для которых .

Теперь рассмотрим режим, когда ЭДС источника (рис. 6.3) изменяется по закону

.

Рис. 6.4. Разряд конденсатора на активное сопротивление

(см. рис.6.3, e(t)=0, Uc(0)=7 в.)

Начальное напряжение на конденсаторе . В этом случае дифференциальное уравнение для напряжения имеет вид:

(6.6)

Решение (6.6) в терминах символьной математики получим с помощью следующей простой программы, содержащей функции dsolve, simple, pretty и ezplot:

>> Uc=dsolve('DUc=-10*Uc+10*(7+5*sin(4*t))','Uc(0)=0');

[Uc,z]=simple(Uc)

pretty(Uc)

ezplot(Uc),grid,axis([0 4 0 15])

ylabel(' Uc(t), B ')

Uc =

7-50/29*cos(4*t)+125/29*sin(4*t)-153/29*exp(-10*t)

z =

collect(t)

50 125 153

7 - -- cos(4 t) + --- sin(4 t) - --- exp(-10 t)

29 29 29

>>

Результат представлен в простом текстовом формате функции pretty, приближенном к математическому выражению. Напряжение на конденсаторе можно рассчитать по следующей формуле:

(6.7)

На рис. 6.5 изображено напряжение, изменяющееся в переходном режиме. Из формулы (6.7) и рис.6.5 следует, что при напряжение равно нулю, а по окончании переходного процесса, когда экспоненциальная составляющая близка к нулю, в цепи устанавливаются периодические колебания с частотой, равной частоте сети, и смещенные по оси ординат на величину напряжения 7В, соответствующую постоянной составляющей источника питания .

Рис.6.5. Переходный процесс в RC –цепи,

e(t) = 7+5*sin(4*t).

Овладев техникой решения дифференциальных уравнений в аналитическом виде, мы получили возможность исследовать переходные процессы в электрических цепях при сложной форме ЭДС источников питания и визуально оценивать результаты с помощью графических построений.

Рассматривая простую RC-цепь, попытаемся определить, как изменяется основная переменная состояния цепи – напряжение на конденсаторе – под действием ЭДС, представляющей собою затухающий периодический процесс

(6.8)

при различных значениях постоянных времени и . В качестве примеров получим решения для напряжения (6.5) со следующим численными значениями коэффициентов:

,

,

.

Параметры электрической цепи (рис. 6.3) сохраняются неизменными.

Расчеты выполним с помощью файла sah353.m.

% File 'sah353.m'

% RC-circuit response plotting:

syms Uc Uc1 Uc2 t;

Uc1=dsolve('DUc1=-10*Uc1+10*10*exp(-t/0.3)*sin(2*pi*t/0.8)','Uc1(0)=0')

[Uc1,z]=simple(Uc1)

pretty(Uc1)

%------------------------------

Uc2=dsolve('DUc2=-10*Uc2+10*10*exp(-t/0.3)*sin(2*pi*t/0.03)','Uc2(0)=0')

[Uc2,z]=simple(Uc2)

pretty(Uc2)

%------------------------------

Uc3=dsolve('DUc3=-10*Uc3+10*10*exp(-t/0.05)*sin(2*pi*t/0.03)','Uc3(0)=0')

[Uc3,z]=simple(Uc3)

pretty(Uc3)

%==========================

tt=0:0.001:1.6;

Vc1=subs(Uc1,'t',tt);

plot(tt,Vc1,tt,10*exp(-tt/0.3).*sin(2*pi*tt/0.8)),grid

xlabel('Time, sec'),

ylabel(' Uc1(t), e(t), B ')

pause

%==========================

tt=0:0.0001:0.4;

Vc2=subs(Uc2,'t',tt);

plot(tt,Vc2,tt,0.1*10*exp(-tt/0.3).*sin(2*pi*tt/0.03)),grid

xlabel('Time, sec'),

ylabel(' Uc2(t), e(t), B ')

pause

%==========================

tt=0:0.001:0.4;

Vc3=subs(Uc3,'t',tt);

plot(tt,Vc3,tt,0.1*10*exp(-tt/0.05).*sin(2*pi*tt/0.03)),grid

xlabel('Time, sec'),

ylabel(' Uc3(t),e(t), B ')

Файл представляется четырьмя блоками. Первый блок содержит заданные символьные переменные, функции dsolve, simple, pretty, используемые в трех частях блока для нахождения аналитических решений в терминах символьной математики, их упрощения и преобразования к удобному для чтения виду. Части блока сформированы по одной схеме и разделены штрих- пунктирными линиями.

Ниже приведен компьютерный вариант решения для переменной состояния при подключении цепи к источнику с напряжением .

Uc1 =

120*exp(-10/3*t)*(-3*pi*cos(5/2*pi*t)+3*exp(-20/3*t)*pi+8*sin(5/2*pi*t))/(64+9*pi^2)

z =

simplify

120 exp(- 10/3 t)

(-3 pi cos(5/2 pi t) + 3 exp(- 20/3 t) pi + 8 sin(5/2 pi t))/(

2

64 + 9 pi )

Напряжение на конденсаторе при воздействии ЭДС источника равно:

.

Графическая интерпретация и выполнена с помощью рис. 6.6. Для построения рисунка предназначен второй блок, где использована команда plot. Чтобы получить массив чисел по вышеприведенной аналитической зависимости, применена функция подстановки subs. Синтаксис

означает, что вектор образован путем подстановки в символьное выражение вместо аргумента вектора чисел , сформированного в строке

.

Вектор чисел, представляющий собой , получен непосредственно путем вычислений в операторе plot.

Рис.6.6. Переходный процесс в RC-цепи.( e(t) = e1(t)).

Вторая часть первого блока в файле sah353.m предназначен для нахождения напряжения при подключении цепи к источнику с напряжением . От первой части он отличается только использованными индексами напряжения и ЭДС. Компьютерный вариант решения выглядит следующим образом:

Uc2 =

(-150*pi*cos(200/3*pi*t)*exp(-10/3*t)+15*exp(-10/3*t)*sin(200/3*pi*t)+150*exp(-10*t)*pi/(1+100*pi^2)+15000*exp(-10*t)*pi^3/(1+100*pi^2))/(1+100*pi^2)

Uc2 =

15*exp(-10/3*t)*(-10*pi*cos(200/3*pi*t)+10*exp(-20/3*t)*pi+sin(200/3*pi*t))/(1+100*pi^2)

z =

simplify

15 exp(- 10/3 t)

(-10 pi cos(200/3 pi t) + 10 exp(- 20/3 t) pi + sin(200/3 pi t))/(

2

1 + 100 pi )

Из выведенного с помощью функции pretty решения видно, что напряжение на конденсаторе при воздействии на цепь равно:

Для графических построений и в файле предусмотрен третий блок, по содержанию аналогичный второму. Отличия состоят лишь в выбранных индексах , , , а также в размерности вектора . Кроме того, выведено на рис. 6.7 при умножении на масштабный коэффициент, равный 0.1. Переходный процесс в цепи представлен на рис. 6.7 с соответствующими пояснениями, выполненными в графическом окне редактора.

Функция в символьной форме, соответствующая подключению RC-цепи к источнику , получена с помощью третьей части первого блока в файле sah353.m, а графические построения реализованы посредством четвертого блока программы. Их построения выполнены аналогично предыдущим вариантам.

Рис. 6.7. Переходный процесс в RC-цепи ( e(t) = e2(t) ).

Приведем фрагмент компьютерного решения как результат действий функции simple() и pretty().

Uc3 =

(-600*pi*exp(-20*t)*cos(200/3*pi*t)+600*exp(-10*t)*pi-90*exp(-20*t)*sin(200/3*pi*t))/(9+400*pi^2)

z =

combine

(-600 pi exp(-20 t) cos(200/3 pi t) + 600 exp(-10 t) pi

2

- 90 exp(-20 t) sin(200/3 pi t))/(9 + 400 pi )

>>

Запишем полученную функцию в аналитической форме:

На рис. 6.7 изображены графики и во временном диапазоне от 0 до 0.4с.

Рис. 6.8. Переходный процесс в RC- цепи ( e(t) = e3(t) ).

Из приведенных расчетов следует, что в зависимости от численных значений коэффициентов, входящих в формулу (6.8), переходные процессы в RC-цепи значительно изменяются. Если на рис. 6.6 представлен переходный процесс, не содержащий явно выраженной периодической составляющей, то рис. 6.7 содержит затухающие гармонические колебания сложной формы. В отдельные моменты кривая располагается ниже оси абсцисс, что свидетельствует об изменении знака напряжения на емкости. На рис. 6.8 представлен случай затухающих колебаний сложной формы, не сопровождающихся изменением полярности напряжения на емкости в течение всего переходного процесса.

Пакет символьной алгебры, как показано в параграфе 6.4, позволяет получать решения в аналитическом виде линейных дифференциальных уравнений высокого порядка. Используя эту возможность пакета, мы определим и в электрической цепи с двумя накопителями энергии (рис. 6.11, см. ниже). Параметры цепи: Ом, , Ом, мкФ, Гн, В, А, В. Коэффициенты модели можно определить по примеру 4 (см. раздел 4.6).

Чтобы получить аналитическое решение в символьных переменных, воспользуемся файлом sah354.m.

% File 'sah354.m'.

% RLC-circuit modeling.

syms I Uc t;

[I,Uc]=dsolve('DI=10*Uc','DUc=-10000*I-100*Uc+100*30','I(0)=0.1','Uc(0)=20');

Ii=simple(I)

Uci=simple(Uc)

% Graphics:

tt=0:0.15/240:0.15;

x1=subs(Ii,'t',tt);

x2=subs(Uci,'t',tt);

plot(tt,x1*20,tt,x2),grid

xlabel('Time , sec. ')

ylabel(' I(t).20,A ; Uc(t),B ')

Файл содержит строку с объявленными символьными переменными, решатель дифференциальных уравнений, функции упрощения полученных основных переменных состояния – тока через индуктивность и напряжения на емкости. С помощью dsolve решается система уравнений:

,

, (6.9)

где В, А, В.

По завершении «работы» файла sah354.m, в режиме прямых вычислений, используя функцию pretty, мы получим следующие аналитические зависимости:

>> pretty(Ii)

1/2 1/2 1/2

3/10 + 1/195 exp(-50 t) (-39 cos(50 t 39 ) + 19* 39 sin(50 t 39 ) )

>> pretty(Uci)

20 1/2 1/2 1/2

-- exp(-50 t) (39 sin(50 t 39 ) + 39 cos(50 t 39 ))

39

>>

Таким образом, ток равен:

.

Подстановкой с помощью приведенной формулы можно получить начальный ток А. Если же переходный процесс практически завершится, то принужденный ток , что, безусловно, следует из топологии цепи (рис. 6.11).

Напряжение на конденсаторе равно:

.

Из приведенной зависимости следует, что при начальное напряжение В, а принужденная составляющая .

Для графических построений в файле sah354.m используются функции подстановки subs (от английского слова substitution). Вместо символьного аргумента производится подстановка вектора , а затем с помощью оператора plot возвращаются графики тока и напряжения, которые представлены на рис. 6.9.

Рис. 6.9. Переходный процесс в RLC- цепи

Приведенные аналитические решения и содержат периодические составляющие, поскольку собственные значения матрицы состояния

являются комплексно-сопряженными величинами:

и .