Уравнение измерителя

и вектор остатков имеет норму

B заключение отметим, что если ранг матрицы H равен n и если чис­ло ограничений-равенств равно l, причем l < n , то наилучшая оценка по критерию J₁ должна выполняться после формирования матрицы размерности (nЧn). B ее составе должны содержаться элементы, вхо­дящие, во-первых, во все l ограничений, а, во-вторых, - коэффициенты уравнений, соответствующих (n-l) наименьшим остаткам, полученным с помощью метода наименьших квадратов. Таким образом, путем использо­вания измерений совместно с ограничениями-равенствами мы получаем полную систему линейных уравнений, решаемую с помощью обращения матрицы . Основное преимущество алгоритма состоит в том, что мы не используем для оптимального оценивания итерационные процедуры, а также методы поиска минимума линейной формы с помощью линейного программирования.

1.8. Нелинейное оценивание параметров моделей в режиме прямых вычислений

Решение нелинейных систем уравнений, как правило, выполняется численными методами. B среде MatLAB для этих целей предлагается более двух десятков различных функций, которые содержатся в подкаталоге "optim". Они условно разделяются на шесть основных групп:

• функции для поиска минимума в условиях ограничений (fminbnd, fmin-con, fminsearch, fminunc, fsemirif);

• вычислительные процедуры для решения минимаксных задач (fminitnax, fgoalattain);

• функции для решения задач методом наименьших квадратов (lsqlin, lsqnonneg);

• вычислительные процедуры, базирующиеся на нелинейном методе наименьших квадратов (lsqcurvefit, lsqnonlin);

• функции для нахождения нулей нелинейных уравнений tfzero, fsolve);

• вычислительные процедуры для решения задач линейного и квадратич­ного программирования (linprog, quadprog).

Практическое использование каждой функции для решения задач высокой размерности требует соблюдения определенных условий и со­ставления вспомогательного файла, к которому совершаются обращения из основного файла в процессе вычислений. Вспомогательный файл принято называть файл-функцией.

C помощью приведенных выше функций может решаться большой класс задач оценивания параметров моделей объектов и систем управления по экспериментальным данным. Расчеты могут выполняться без составления скрипт-файлов и файлов-функций, т.е. производиться в режиме пря­мых вычислений.

Остановимся на случае статики (одношаговом процессе). Предполо­жим, что нелинейная модель измерителя можно представить уравнением

(1.64)

где – у_i - i - oe измерение,

x - (n Ч 1) - вектор параметров,

h(x) - нелинейная скалярная функция, соответствующая i - му измерению состояния,

v_i - ошибка измерения с нулевым средним и дисперсией .

Имея в наличии т измерений и n переменных состояния и переопре­деленную систему (m > n), мы можем для оптимальной оценки предложить метод наименьших квадратов со взвешиванием измерений. Заметим, что в общем случае, когда необходимо оценивать x в условиях ограничений, процедура оценки может быть сформулирована в терминах задачи матема­тического программирования.

Введем критерий качества

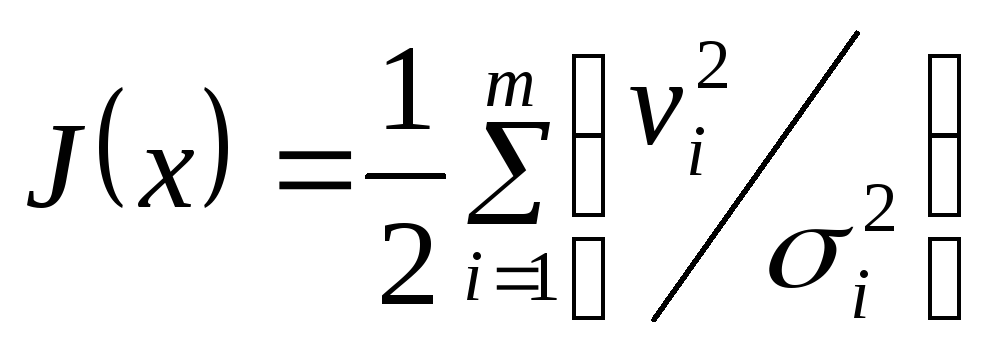
и предположим, что выбор x необходимо произвести при соблюдении ог­раничений в форме равенств и неравенств

(1.65)

которые отвечают технологическим условиям работы судовых систем управления. Тогда оценка состояния может быть выполнена в результате решения следующей задачи математического программирования:

минимизировать (1.66)

при ограничениях (1.65).

Поиск оптимального решения (1.66) при соответствующих ограничениях - непростая техническая задача, относящаяся к среднеквадратич­ным проблемам с нелинейными ограничениями и решаемая обычно только численными методами [42]. B отличие от полиномиальных функций, решение для которых может быть найдено не всегда даже численными методами, квадратичные формы обладают свойствами унимодальности. Поэтому в классе решаемых задач оценивания мы можем найти единственное x, отве­чающее условиям минимума.

Для получения оптимальной оценки вектора состояния мы рекомен­дуем использовать функцию "lqcurvefit" содержащуюся в пакете MatLAB. He останавливаясь на ее описании, приведем последовательность опера­ций, необходимых для использования "lsqcurvefit". Рассмотрим следующий пример. Допустим, что

(1.67)

где bet - вектор, представляющий угол (в радианах) и соответствующий вектору alf = [0 30 60 90 120 150].

C помощью формулы (1.67) рассчитаем f(bet), которые образуют вектop y размерности (1Ч6). Будем полагать, что в формуле (1.64) ошибкой из­мерения можно пренебречь, т.е. измерения практически совпадают с элемен­тами y, определенными по формуле (1.64). Задача состоит в получении наи­лучшей оценки амплитуды гармонического сигнала y(alf) и его аргумента по вектору измерений. Приведем ее решение в режиме прямых вычислений:

>> alf=0:30:150;

>> bet=alf.*(pi/180);

>> y=5*sin(bet+28*(pi/180));

>> xdata=bet; ydata=y;

>> fun=inline('x(l)*sin((xdata)+x(2))','x','xdata');

>> x=lsqcurvefit(fun,[2 O.3],xdata,ydata)

Optimization terminated successfully:

Relative function value changing by less than OPTIONS. TolFun

x=5.000 0.4887

>> Xalf=x(2)*180/pi

Xalf=28.000

>>

B качестве комментария к полученному решению следует отметить, что мы использовали для формирования функции "fun" объект класса "inline". Объекты этого класса - функции, заданные в символьном виде, что позволяет обращаться к ним как к математическим объектам. Каталог класса "inline" можно отнести к объектно-ориентированному программи­рованию. Аргумент приведенной функции здесь определяется автоматиче­ски, путем поиска в составе выражения одноместных символов. B нашей задаче в качестве аргумента функции используется символ 'x', состоящий из элементов х(l) и x(2).