0. 1.4. Рекуррентный метод оценивания параметров моделей

Важным свойством (1.15) является возможность значительного уп­рощения вычислительной процедуры путем использования рекуррентной схемы, исключающей необходимость инверсии гауссовской нормальной матрицы полной размерности.

Возвращаясь вновь к модели измерителя (1.11), запишем матричное уравнение, соответствующее т измерениям, с индексами (m)

(1.28)

Так как учет результата каждого последующего измерения связан с изменением числа строк матрицы H и размерности векторов у и v, то, во­обще говоря, оценка может производиться с помощью (1.15). Если при этом воспользоваться методом наименьших квадратов со взвешиванием измерений, то критерий качества

(1.29)

содержащий ковариационную матрицу, принимает минимальное значение, если оценка x выполняется путем решения матричного уравнения

(1.30)

Индекс означает, что оценка размерности (nх1) производится

по т измерениям (априорное оценивание).

Предположим, что выполнено (m+1) - oe измерение у_т+1, Н_m+1 и v_m+1 . То­гда новое измерение, согласно (1.28), можно представить с помощью уравнения

(1.31)

Присоединим (1.31) к системе (1.28) с помощью блоков

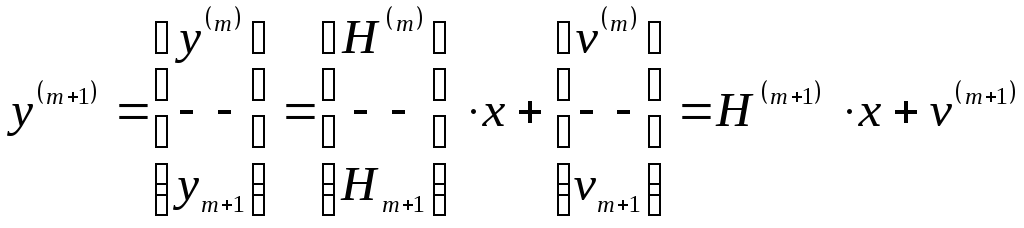(1.32)

Новая апостериорная оценка состояния должна производиться по числу измерений, использованных в (1.32):

(1.33)

Размерность вектора оцениваемых параметров (переменных состоя­ния) с добавлением новых измерений не изменяется. Однако численные значения его элементов зависят от присоединенных данных. Тот факт, что добавление каждого нового результата измерений требует повторного вы­полнения всех операций, определенных (1.33), свидетельствует о возрас­тании объема вычислений с увеличением размерности матрицы H. Вместе с тем, объем рутинных вычислений можно значительно уменьшить, если новые измерения учитывать как поправки, вносимые в значения уже имеющихся оценок. При этом исключается необходимость операций над матрицами высокой размерности; соответственно, повышается эффектив­ность вычислительных алгоритмов и машинных программ, используемых в

процессе управления технологическими комплексами. Для получения эф­фекта взвешивания измерений с помощью элементов ковариационной матрицы необходимо разделить на блоки соответствующих размерностей

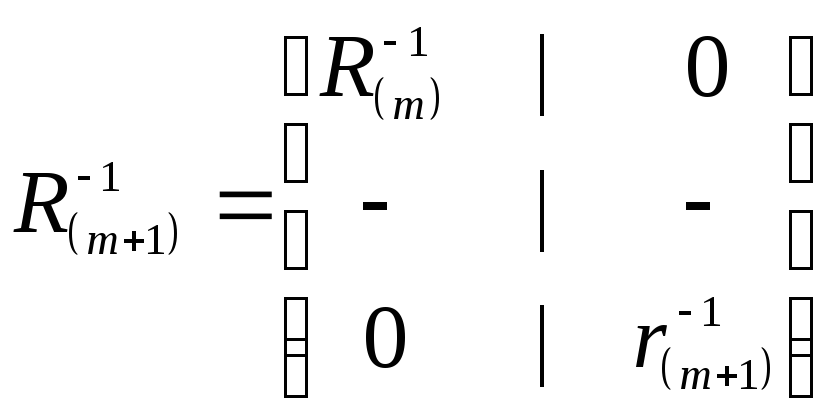(1.34)

т.е., согласно (1.34) не производится взвешивания произведения ошибок на первых т и последующих измерениях. Взамен же получаются эффек­тивные вычислительные алгоритмы, уменьшающие объем вычислений, выполняемых в процедурах оценивания, на несколько порядков.

Используя существующие методы преобразования блочных матриц, можно преобразовать информационную матрицу, входящую в уравнение (1.33), к следующему виду [27]:

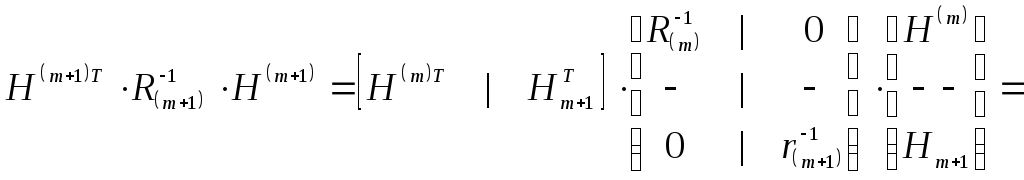(1.35)

Введем обозначения:

и

тогда уравнение (1.35) можно записать

а инверсия

(1.36)

Применив к (1.36) лемму об обращении матриц, содержащуюся в работе [9], получим рекуррентную формулу

(1.37)

Если вектор измерений у_{т+ 1} в уравнении (1.4-4) вырождается в ска­лярную величину, то матрица также будет скаляр­ной величиной, и, следовательно, ее обращение не представляет труда.

Если, например, и , то (1.37) принимает вид

(1.38)

Получен очень полезный результат, поскольку для нахождения но­вой оценки нет необходимости в инвертировании матрицы большой раз­мерности с присоединением новых измерений. Новая оценка состоит из оценки на предыдущем шаге, с которой суммируется поправочный коэф­фициент, полученный по измерениям y_{m+ 1} ,  и M_m :

(1.39)

Возвращаясь к разности между оценочным и истинным значениями параметров и переходя к осредненным оценкам, можно определить ко­вариационную матрицу с помощью формулы

(1.40)

Используя (1.40), мы также можем получить рекуррентное соот­ношение, подобное (1.38) для :

(1.41)

Нетрудно заметить, что ковариационная матрица согласно(1.41), с увеличением т всегда уменьшается и в пределе стремится к нулю. Следовательно, оценка является не только несмещенной, но и состоятельной - это является исключительно важным свойством метода наименьших квадратов.

Рекуррентное оценивание начинается с заданных значений x₀ и M₀. Если они не заданы, а имеется в наличии система из n уравнений, следует получить M_n , х_n , а затем с помощью (1.30) выполнить последующие оценки.

Для получения рекуррентного алгоритма в общем случае (для вектора y_m+1) введем обозначение части второго слагаемого (1.37):

Поскольку уравнение (1.33) можно записать в виде

то, подставляя в него выражение (1.37), можно записать

Обращаясь вновь к специально выбранной форме ковариационной матрицы (1.33), с учетом того, что произведение

можно получить оценку в виде

Это выражение, представляющее собой рекурсивный оцениватель, получено с учетом того, что если в предшествующей формуле первое сла­гаемое в правой части умножить на М_m, оно будет представлять оценку (без учета новых данных).

Необходимо отметить, что каждое последующее значение оценки следует производить по предыдущей с добавлением поправки, зависящей от размерности у_(m+1) и ожидаемого значения

"Работу" рекурсивного оценивателя продемонстрируем на следую­щем примере.

Предположим, что требуется оценить коэффициенты модели

по следующим экспериментальным данным в пяти точках на плоскости (x,y):

(0, l); (l, 2); (2, 4); (4, 5); (5, 6).

Сформируем матрицу H и вектор у:

Будем считать, что требуется рекурсивно оценить коэффициенты а и b по следующим данным:

на первом шаге

на втором шаге

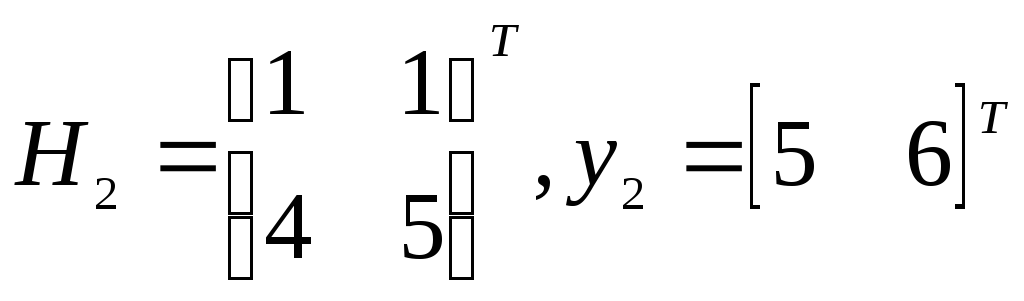
Решение выполним для и

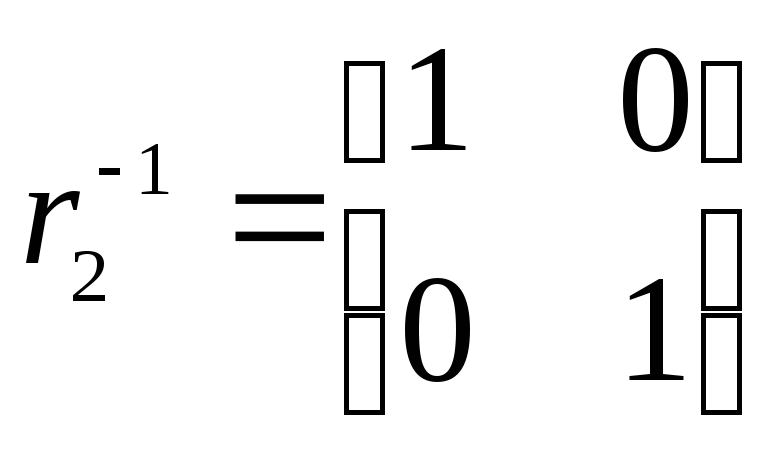
Для оценки используем операцию левого деления

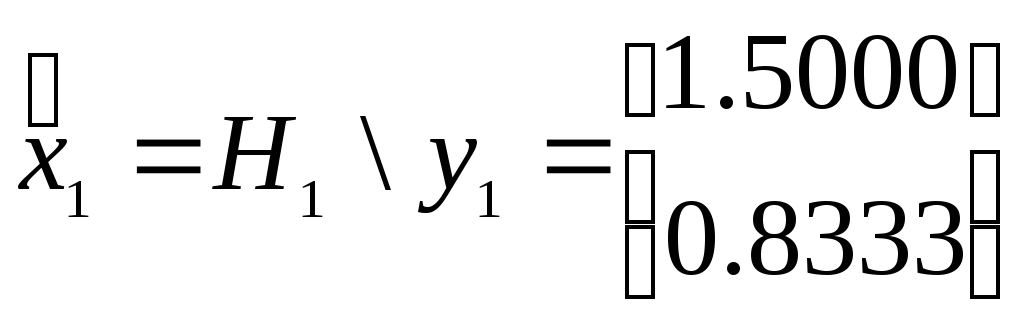
Затем определим M₁:

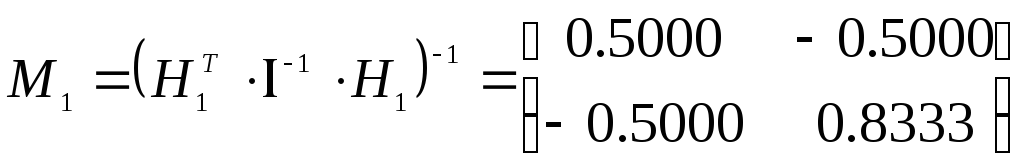
Для расчета M₂ по формуле (1.4-10) предварительно найдем матрицу D

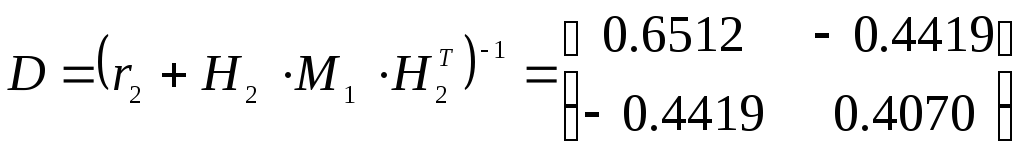
Используя D, получим

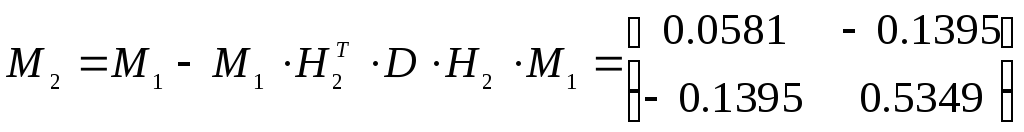
Оценка коэффициентов а и b на втором шаге, согласно уравнению рекурсивного оценивателя, будет состоять из оценки x₁ и дополнительной составляющей, определяющей "вклад" экспериментальных данных на вто­ром шаге. Поскольку , для оценки используем выражение

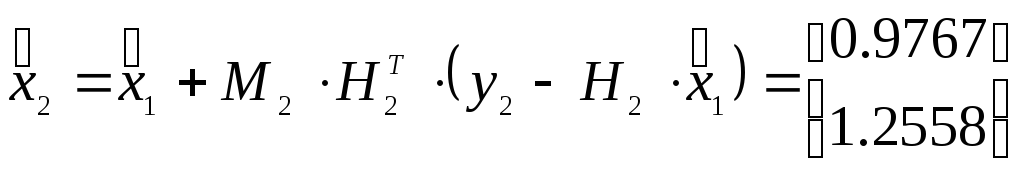
Для вычислений мы предлагаем фрагмент программы, содержащий исходные данные, из которых путем "вырезки" из матрицы H получены H₁, H₂, y₁ и у₂. По приведенным выше соотношениям рассчитаны M₁, D, М₂ и получены и .

Рекуррентньм метод оценивания параметров

y = [l 2 4 5 6]';H = [0 1 2 4 5; 1 1 1 1 1]^’;

Hl = H (l:3,: );

H2 = H (4:5,: );

yl = y (l:3);

y2 = y (4:5);

Ml = inv (Hl' *Hl);

D = inv ([l 0; 0 l]+Hl*Ml*H2');

M2 = Ml-Ml*H2'*D*H2*Ml;

Вычисление оценок:

xl = Hl\yl;

x2 = xl+M2*H2'*(y2-H2*xl)

Проверка решения выполнена путем использования прямой оценки по формуле

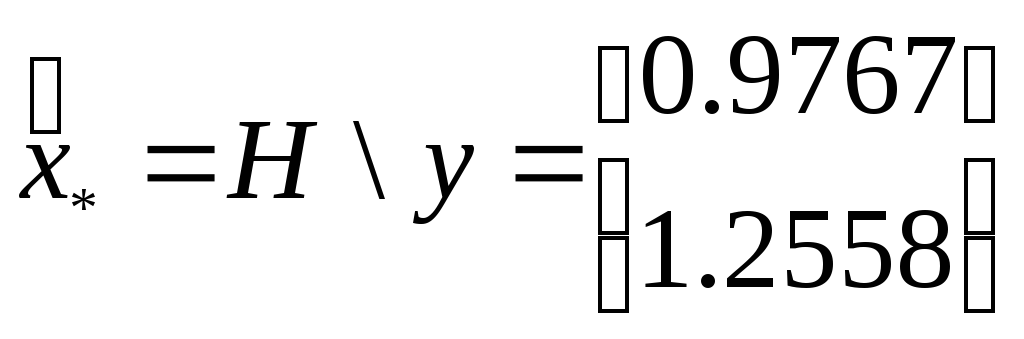
Этот результат эквивалентен .

Таким образом, модель имеет вид