5.3.Матричная форма решения уравнений состояния динамических систем

Рассмотрим модель системы, описываемую матричным уравнением:

, (5.0)

Запишем матричную экспоненту в виде , а также воспользуемся ее инверсией . Заметим, что – единичная матрица. Так как: 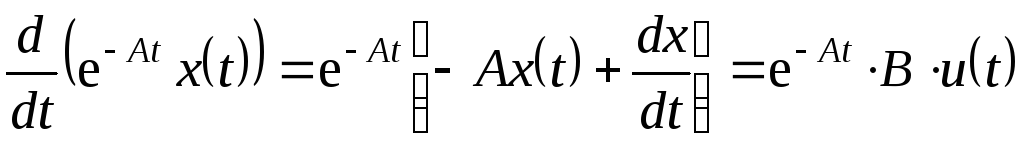, то (5.17) можно записать:

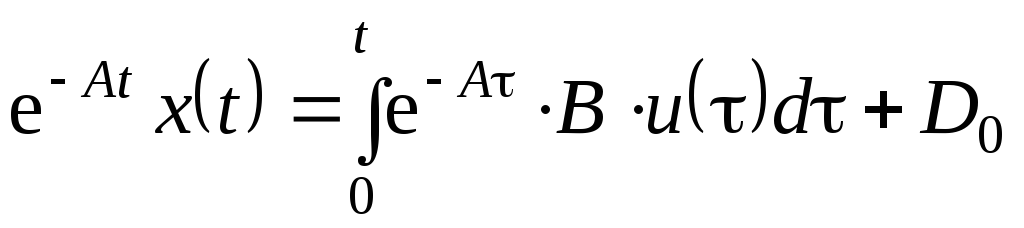, (5.0)

где – постоянная интегрирования. Умножим (5.18) слева на матричную экспоненту. Тогда

.

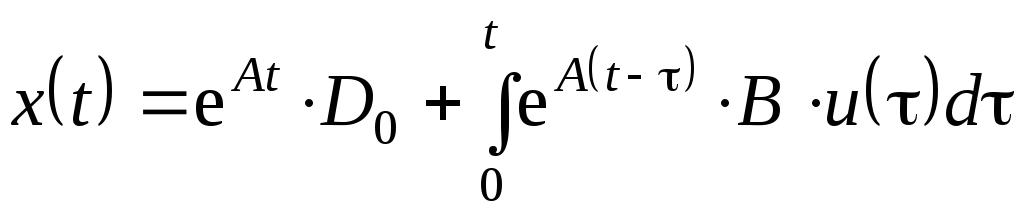При значение интеграла равно нулю и, следовательно, . Вектор состояния

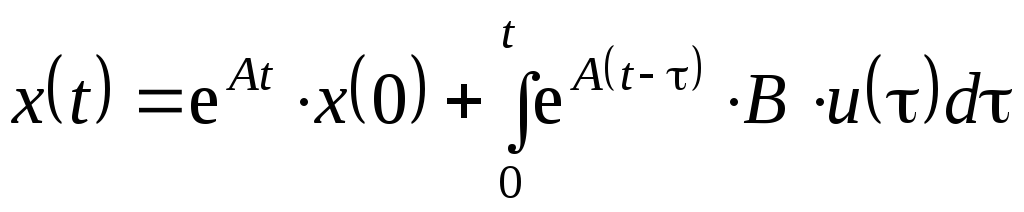(5.0)

Матричную форму записи (5.19) мы будем неоднократно использовать в дальнейшем. Поэтому остановимся на рассмотрении некоторых деталей.

Если на систему не оказывается никаких внешних воздействий, то есть в любой момент времени вектор управления равен нулю, то интеграл также равен нулю. Тогда решение (5.19) вырождается и имеет вид:

(5.0)

Очевидно, переходный процесс в системе (5.20) может наблюдаться только в том случае, если хотя бы один из элементов вектора не равен нулю. Физическая интерпретация этого условия состоит в наличии запасов энергии в системе (кинетической и потенциальной) в момент . Если является матрицей Гурвица, то есть ее собственные значения содержат вещественные отрицательные части чисел, то вектор при стремится к нулю. Иначе говоря, по окончании переходного процесса система переходит из начального состояния в начало координат .

В приложении к электрическим цепям означает наличие напряжений на емкостях и токов через индуктивности в момент , которые, в свою очередь, характеризуют энергию электрического поля конденсаторов и магнитного поля индуктивных катушек. Второе слагаемое в (5.19), выраженное интегралом, характеризует влияние на поведение системы внешних воздействий в форме вектора управления , не равного нулю. Необходимо отметить, что интегрирование ведется только по переменной .

Особый интерес представляет режим, соответствующий . Например, если электрическая цепь подключается к источникам постоянных ЭДС и токов, то, как было показано в главе 4, вектор (в механических системах аналогичные режимы наблюдаются тогда, когда на систему воздействуют постоянные силы).

Уравнение (5.19) можно привести к виду:

(5.0)

Уравнение (5.21) целесообразно использовать для расчета переходных процессов, поскольку в алфавите MatLAB содержится матричная экспоненциальная функция . С помощью MatLAB можно также получить функцию обращения матрицы , функцию формирования единичной матрицы требуемой размерности , возвращающую квадратную единичную матрицу размерности . Иначе говоря, уравнение (5.21) решается без интегрирования дифференциальных уравнений, но только в тех случаях, когда является неособенной матрицей. Последнее ограничение является существенным.

4. Моделирование динамических систем с двумя накопителями энергии при параметрических возмущениях Для определенности рассмотрим модель динамической системы с двумя накопителями энергии:

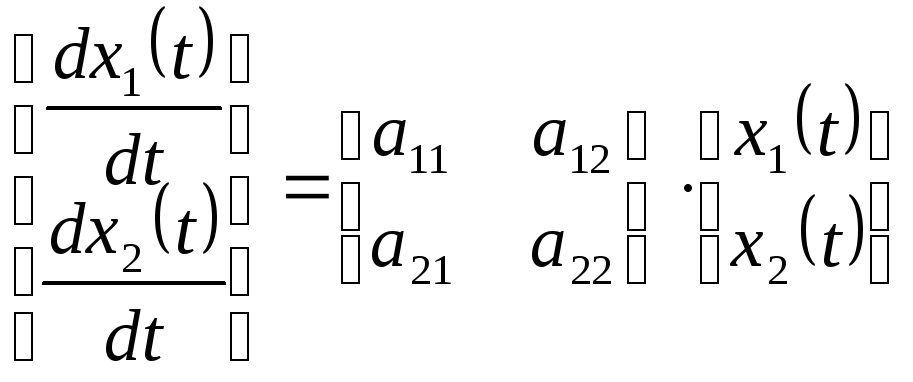, при .

Динамические свойства системы определяются собственными значениями матрицы . Модели для различных собственных значений мы можем получить путем возмущения параметра . Выберем , , и сохраним их на всех режимах постоянными. В таблице 5.1 приведены собственные значения матрицы A, изменяемые в диапазоне – от чисто мнимых до вещественных отрицательных и неравных собственных чисел - путем вариации .

Таблица 5.1

№ режима

Режим №1 моделируется при чисто мнимых корнях. Режимы 26 характеризуются тем, что корни являются комплексно-сопряженными с отрицательными вещественными частями. Режим №7 соответствует кратным корням. Наконец, режим №8 моделируется при вещественных отрицательных и неравных корнях.

Моделирование произведем на всех режимах при ненулевых начальных условиях. Пусть вектор . Основная программа для моделирования восьми режимов представлена файлом , а вспомогательная – файлом

Файл

%Investigation of the second-order electric circuits.

%The main file "mmm13.m" and the complementary file "sah35.m".

Echo off

clc

t0=0;

tfinal=40;

y0=[2.5 12.5]';

%[t, y]=ode23('sah35', t0, tfinal, y0);

tol=1.e-3; %Accuracy

trace=-2.2;

[t, y]=ode23('sah35', t0, tfinal, y0, tol, trace);

subplot(223)

plot(t, y), title('Circuits time history'), grid,

pause,

subplot(224)

plot(y(:,1), y(:,2)), title('Phase plane plot'),

grid,

pause

Файл

%File "sah35.m".

%The behavior of dynamical system (electrical circuit) model.

%Two energy capacitance.

function yprime=sah35(t, y);

%This program is auxiliary and implemented with the

%main program (file "mmm13.m").

%Matrix coefficients: a11=0, a12=1, a21=-1, a22=-2.5

yprime=[0 1; -1 -2.5]*[y(1) y(2)]'+[1 0]'*4*0;

Содержание основной программы в целом повторяет ранее описанную программу (файл ). Здесь также используется внешний файл . Отличие состоит только во введении операторов смены графических окон и , которые позволяют вывести соответствующие кривые на экран в малые графические окна, составляющие по размерам ј экрана. В частности, и размещают два окна в верхней половине экрана, а первоначально приведенные и размещают графики в двух окнах, расположенных в нижней половине экрана дисплея.

Вспомогательный файл , содержащий функцию, представленную в виде матричного уравнения (5.17), за счет принятого равным нулю вектора управления (последняя строка программы) позволяет решать дифференциальное уравнение

при заданном , где на каждом режиме принимает значения, приведенные во втором столбце таблицы 5.1.

Результаты моделирования представлены на рисунках (5.35.10)

Для каждого режима приведены временные характеристики и фазовый портрет. Видно, что при чисто мнимых корнях (режим №1) энергия в системе не рассеивается, и колебания переменных состояния являются гармоническими (с неизменной амплитудой). На фазовой плоскости этому режиму соответствует замкнутая кривая.

Режимы 26 при соответствующих комплексно-сопряженных корнях (см. таблицу 5.1) представляют собой затухающие колебания. Чем больше по абсолютному значению коэффициент , то есть , тем быстрее затухают периодические колебания и тем меньше собственная частота. В режиме №8 процесс становится апериодическим (модель апериодического звена второго порядка, рис. 5.10). Коэффициент характеризует скорость рассеяния энергии в системе. Чем он больше (по модулю), тем быстрее затухает переходный процесс.