3. Динамические звенья и системы под воздействием гармонических сигналов

В этой главе приведены простые программы, позволяющие выполнять расчеты частотных характеристик динамических звеньев и систем, а также исследовать резонансные явления с помощью системы MatLAB.

3.1.Построение частотных характеристик простых динамических звеньев

Любая линейная система, моделью которой являются дифференциальные уравнения с постоянными коэффициентами, может быть разделена на элементарные звенья с известными динамическими свойствами. Звенья имеют различные передаточные функции и отличаются по виду переходного процесса. Типовыми звеньями являются: апериодическое (первого и второго порядков), колебательное, интегрирующее, дифференцирующее, усилительное, звено с чистым запаздыванием и другие.

Усилительное звено (в идеальном случае) позволяет воспроизвести входной сигнал без искажения его формы. Другие динамические звенья, содержащие в своей структуре элементы-накопители энергии, воспроизводят входной сигнал, изменяя его форму. Каждое динамическое звено является своеобразным фильтром [2]. Если на вход такого звена подавать гармонический сигнал с изменяющейся частотой, но постоянной амплитудой, то на выходе в установившемся режиме каждой частоте входного сигнала будет соответствовать выходной сигнал той же частоты. Однако амплитуда и фаза выходного сигнала будут изменяться в функции частоты.

Рассмотрим построение частотной характеристики апериодического звена с передаточной функцией [28]

, (3.0)

где – постоянный коэффициент; – постоянная времени; – оператор Лапласа.

Амплитудно-фазовая характеристика апериодического звена получается заменой в формуле (3.1) оператора где . Тогда комплексный коэффициент передачи:

(3.0)

Амплитудно-фазовая характеристика (3.2) устойчивого апериодического звена представляет собой окружность с центром на вещественной оси в точке . Характеристика для всех располагается справа от мнимой оси (в четвертом квадранте).

Обычно для исследования устойчивости систем удобно использовать логарифмические частотные характеристики.

Построение логарифмических частотных характеристик существенно упрощается, если пользоваться приближенным способом их построения, основанным на их представлении в виде отрезков сопрягающихся друг с другом прямых.

Определим логарифмические частотные характеристики апериодического звена (3.1), воспользовавшись данными, приведенными в работе профессора Ли Минг Сена ( [28],с. 60-63):

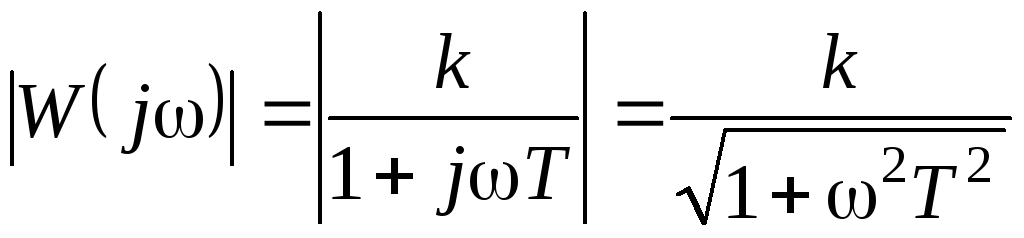(3.0) (3.0)

При модуль комплексного коэффициента передачи (3.3) равен , а на частоте его значение равно . Аргумент равен . Нетрудно видеть, что если , а угол .

Логарифмические амплитудная и фазовая частотные характеристики апериодического звена определяются выражениями:

(3.0) (3.0)

Если и , то, согласно (3.5), будем иметь

(3.0)

Если и , логарифмическая амплитудная характеристика

(3.0) Если , то . (3.0)

Соотношения (3.7), (3.8) и (3.9) показывают, что логарифмическая амплитудная характеристика апериодического звена приближенно может быть представлена двумя прямолинейными отрезками (асимптотами): , если ,

, если ,

сопрягающимися друг с другом на частоте .

Максимальная ошибка сопряжения на частоте равна .

Необходимые расчеты и построение логарифмических амплитудной и фазовой частотных характеристик при и могут быть выполнены с помощью простой программы, представленной файлом .

Остановимся на его содержании. В первых трех строках файла, начинающихся со знаков «%», приведены краткие комментарии. В четвертой строке введено мнимое число, поскольку вычисления выполняются с комплексными числами. Дословно это означает: число есть квадратный корень из . Далее перейдем к описанию программы, пропустив временно пятую и шестую строки. В седьмой строке задается цикл с помощью оператора . Здесь – переменная с минимальным значением 0,01 и шагом дискретности 0,01 (следующее число, отделенное от первого знаком «:») и конечным значением 10. Оператором в восьмой строке вычисляются: модуль комплексного числа (3.2) с помощью алгебраической функции , десятичный логарифм модуля – с помощью функции , который, согласно (3.5), умножается на число 20. Аргумент вычисляется с помощью оператора в девятой строке. Угол представлен в градусах. Здесь есть обозначение числа , принятое в системе MatLAB.

Файл

%File 'sah20'

%Frequency characteristics.

%Example submitted by prof. Lee Ming-Sen

g1=[];

g2=[];

for t=0.01:0.01:10;

z1=20*log10(abs(1/(1+t*i)));

z2=(180/pi)*(angle(1/(1+t*i)));

g1=[g1;z1]; g2=[g2;z2];

end,

t=0.01:0.01:10;

plot(t, g1, t, g2);

semilogx,

grid

pause

%Resonance.

clg;

MV=[0, 2.5, 0, 5.0];

axis(MV)

plot(2.5, 5.0)

hold on

for gam=0:0.1:0.5;

clear w;

lam1=[];

for w=0:0.01:2.5;

lam=1/(sqrt((1-w^2)^2+(gam^2)*(w^2)));

lam1=[lam1; lam];

end;

w=0:0.01:2.5;

plot(w, lam1), grid,

end;

pause,

hold off;

axis('normal');

Теперь возвратимся к пятой и шестой строкам программы. Напомним, что система MatLAB выполняет операции над векторами и матрицами. Поэтому в результате вычислений по циклу необходимо сформировать два вектора – вектор и вектор . До начала цикла возьмем два «пустых» вектора, которые с помощью операторов в десятой строке на каждом шаге вычислений дополним данными и . Цикл завершается оператором , закрывающим рабочее поле оператора .

Для графического отображения логарифмической амплитудной и фазовой частотных характеристик используется оператор , обеспечивающий построения графиков и . Напомним, что аргумент необходимо указывать перед каждой функцией . Для введения логарифмического масштаба по оси абсцисс, в следующей строке используется оператор , а для нанесения координатной сетки – оператор . Оператор прерывает вычисления и сохраняет изображение на экране до нажатия любой клавиши.

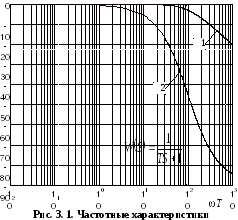
Результаты вычислений по программе представлены на рис. 3.1, где кривая 1 – логарифмическая амплитудная характеристика, а кривая 2 – фазовая частотная характеристика. Так как по оси абсцисс частота отложена в логарифмическом масштабе, становится ясным, почему минимальное значение частоты в цикле принято равным 0,01.