2.7. Модель оценки элементов матрицы преобразования

координат при управлении промышленным роботом

Изложенные в первой главе методы оценки параметров моделей систем широко используются для решения практических задач, связанных с обработкой результатов измерений при наличии помех. Покажем, каким образом процедуры МНК можно применить для повышения точности позиционирования промышленных роботов-манипуляторов в системах компьютерного управления энергоемкими технологическими процессами на водном транспорте.

Промышленные роботы и манипуляторы способны выполнять сложные пространственные перемещения тяжелых грузов при выполнении грузовых операций в портах, обеспечивать высокое качество тепловой резки металлов, производить сварочные работы на судостроительных и судоремонтных предприятиях, осуществлять сборочные и тяжелые рутинные операции при создании и ремонте судовых механизмов и машин, выполнении технологических операций в агрессивных средах, на больших глубинах при освоении шельфа и др.

Компьютерное управление промышленным роботом связано с реализацией траекторных процессов и изменением пространственно-временных координат, в которых осуществляется перемещение его рабочих органов, в том числе - при выполнении операций по смене захвата. Операторы, осуществляющие управление робототехническим комплексом, для получения высокой точности выполнения технологических операций должны производить калибровку, что связано с обеспечением соответствия координат точки робота на рабочей плоскости координатам компьютерной системы [50]. При изменении положения робота на плоскости и, в частности, назначении очередного рабочего участка для выполнения технологических операций требуется «перенастраивать» координаты в рабочей области и приводить их в соответствие с координатами . Назначение новых координат необходимо производить в случаях, когда требуется обеспечить прецизионное управление приводами звеньев робота, а также при появлении ошибок, вследствие нагрузок и увеличения зазоров в сопрягающихся деталях.

Для задания осей координат в базисе рабочего пространства робота выберем три точки , и таким образом, чтобы каждая пара точек , и , образовывала прямоугольную систему координат, в которой должны располагаться все точки траектории движения робота. Поскольку каждой точке траектории движения робота должна соответствовать точка компьютерного управляющего комплекса, обеспечивающего управление приводами звеньев и вывод траекторного процесса на дисплей, то задаваемые координатные оси должны быть представлены своим -эквивалентом. В компьютерном базисе можно задать оси прямоугольных координат с высокой точностью, таким образом, что точкам в базисе робота будут соответствовать [50] :

- начало координат

- расстояние от начала координат по оси

- расстояние от начала координат по оси

Для однородных координат в различных базисах по трем приведенным выше парам точек может быть установлена матрица преобразования , обеспечивающая линейную связь для всего множества и с помощью соотношения:

, где (2.61)

Элементы матрицы определяются в результате решения уравнений

(2.62)

(2.63)

(2.64)

Нетрудно видеть, что условия (2.62), (2.63) и (2.64) выполняются однозначно, если

, , ,

,

,

,

,

.

Матрица преобразования имеет вид

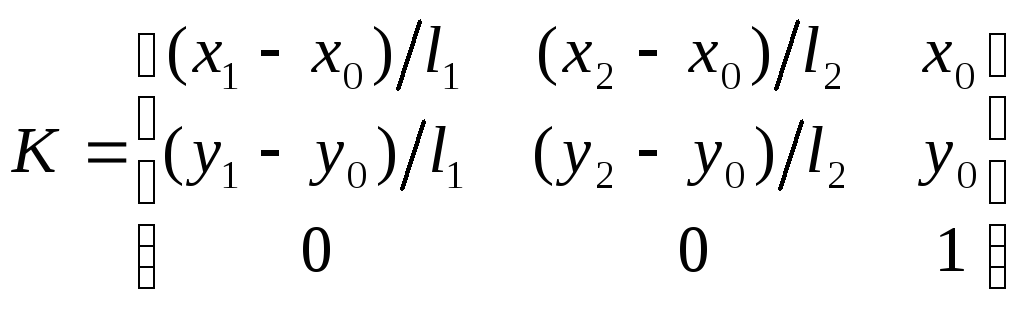. (2.65)

Заметим, что (2.65) является матрицей полного ранга, и поэтому возможно вычисление по измеренным и наоборот. Согласно (2.61), будем иметь

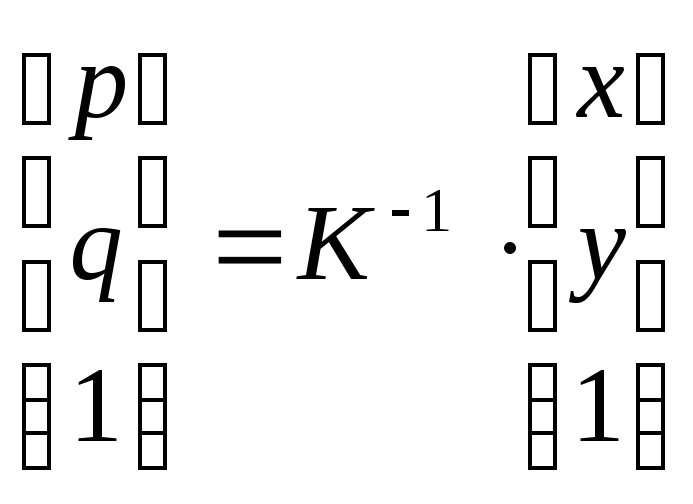. (2.66)

Однако в «жесткой» системе уравнений при наличии погрешностей в процессе измерений полностью сохраняется эта погрешность в матрице K. Она без коррекции будет линейно преобразовываться с помощью (2.66). Вместе с тем, при наличии дополнительных измерений в точках и определении им эквивалентных координат в базисе возможно получить переопределенную систему уравнений для оценки элементов матрицы и, таким образом, минимизировать вектор среднеквадратической ошибки.

Рассмотрим процедуру оценки.

Предположим, что элементы матрицы необходимо получить по парам измерений координат в базисах управляющего компьютера и робота . Введем матрицы размерности :

, .

Тогда оценка элементов , минимизирующая среднеквадратическую ошибку измерений, может быть произведена по формуле

(2.67)

Процедура оценки по формуле (2.67) эквивалентна алгоритму идентификации параметров дискретной динамической системы, рассмотренному ранее в работе авторов [22].

Приведем пример. Оценим элементы для следующих измерений:

,

.

Используя формулу (2.67), выполним оценки элементов матрицы преобразования координат. В результате (в полном формате) будем иметь

,

после чего можно возвратиться к формулам (2.61) и (2.66) для выполнения практических расчетов, которые в среде MatLAB могут быть выполнены в режиме прямых вычислений.

Теперь оценим элементы матрицы и положения осей , только по измерениям, произведенным по расположенной системе точек на выделенной плоскости. Пусть для получены численные значения векторов

Образуем матрицы и и убедимся в том, что по формуле (2.67) вновь получается ранее приведенное .

Далее, выбрав и , рассчитаем для точек в базисе

, и

соответствующие им точки в базисе :

- начало координат,

- точка на оси ,

- точка на оси .

Задачу аппроксимации траектории движения робота предлагается решать в такой последовательности. Сначала в координатах необходимо назначить интерполяционных узлов. Затем с помощью матрицы преобразования требуется найти их эквиваленты в координатах и построить сплайн, по которому следует управлять приводами робота. Затем сплайн, эквивалентный найденному в координатах робота определяется с помощью .

Для выполнения расчетов матриц преобразования и сплайнов составлен скрипт-файл в среде MatLAB, фрагмент которого приводится ниже.

% Прецизионное управление роботом-манипулятором.

% ПОСТРОЕНИЕ СПЛАЙНОВ

%...........................................................

% Оценка элементов матрицы преобразования K по измерениям

% в четырех точках:

p=[0.0000 16.6000 29.3550 0.0000];

q=[0.0000 0.0000 13.1500 13.2300];

x=[209.7900 -211.9894 -533.1908 212.6903];

y=[594.5431 589.9058 251.2447 257.4065];

PQ=[p;q;ones(1,4)]

XY=[x;y;ones(1,4)]

K=inv(PQ*PQ')*PQ*XY'

pause

%K'=[-25.408397 0.219219 209.789976;

% -0.279355 -25.482732 594.543059;

% 0.000000 0.000000 1.000000]

%***********************************************************

% СПЛАЙН-АППРОКСИМАЦИИ

% Интерполяционные узлы в координатах (X,Y):

Xs=[70.0 6.6 -120.3 -247.1 -310.5 -373.7 -405.3 -436.7 -468.0 -499.0]

Ys=[593.0 587.2 565.4 538.5 517.5 486.2 460.4 421.8 370.5 280.9]

% Расчетные значения интерполяционных узлов в базисе (P,Q):

PQs=inv(K')*[Xs;Ys;ones(1,10)];

Ps=PQs(1,:);

Qs=PQs(2,:);

% Построение сплайна в базисе (P,Q):

ps_int=[5.5:0.1:28.0];

qs_int=spline(Ps,Qs,ps_int);

v=size(ps_int);

% Сплайн в базисе (X,Y):

XYspline=K'*[ps_int;qs_int;ones(1,v(2))];

% Графические построения:

subplot(211)

plot(Ps,Qs,'.',ps_int,qs_int),grid

xlabel('Ps'), ylabel('Qs')

pause

subplot(212)

plot(-Xs,-Ys,'.',-XYspline(1,:),-XYspline(2,:)),grid

xlabel('-Xs'), ylabel('-Ys')

Первый блок файла предназначен для оценки , а второй – для сплайн аппроксимации траектории движения.

На приведенном рис.2.12 (в верхней части) в координатах строится график, на котором точками нанесены координаты интерполяционных узлов, а сплошной линией – сплайн. В нижней части рис.2.12 представлен эквивалент этого графика в -базисе. Видно, что матрица обеспечивает линейные

Рис. 2.12. Узлы интерполяции и сплайны в (P_s,Q_s) и (X_s,Y_s )- базисах

преобразования, которые связаны с процедурами растяжения и сжатия координат точек одного базиса относительно другого.