6.6. Операторный метод расчета переходных процессов с использованием пакета символьной математики

Известно, что операторный метод позволяет перевести решение поставленной задачи из области функций во временной области - оригиналов – в область их изображений . Благодаря алгебраической записи исходных уравнений, выполняемой путем перехода к их изображениям, решение становится более простым. Алгебраические уравнения, содержащие также начальные условия, затем решаются относительно искомых переменных. Полученное решение в области изображений затем вновь переводится в область оригиналов, т.е. во временную область.

Функциональным преобразованием для перехода от оригиналов к изображениям чаще всего является преобразование Лапласа.

Получение изображения для заданной функции во временной области носит название прямого преобразования Лапласа и состоит в определении интеграла

, (6.10)

где - комплексный параметр преобразования – оператор Лапласа. Между операторной формой записи функции и функцией во временной области , очевидно, нельзя использовать обычный знак равенства, а можно лишь говорить о соответствии функций. Синтаксис соответствия определяется знаком соответствия. Соответствие между оригиналом и изображением записывается в следующей форме:

или .

Исключительно важное свойство преобразования Лапласа состоит в том, что оно позволяет производные и интегралы функций во временной области представить алгебраическими функциями в области изображений, с учетом начальных значений самих функций. Таким образом, интегро-дифференциальные уравнения в области изображений становятся алгебраическими. Решая эти алгебраические уравнения, находят сначала изображения функций. Затем с помощью обратного преобразования Лапласа получают эти функции во временной области.

Основная трудность в использовании операторного метода расчета переходных процессов состоит в необходимости решения уравнения (6.10) для широкого класса функций . Обычно такие решения представляются таблицами преобразований Лапласа. Конечно, для ряда простых функций интеграл может быть определен обычными методами интегрирования, изучаемыми в учебных курсах интегрального исчисления. Однако, такое решение может быть получено не всегда. К тому же оно, как правило, связано с необходимостью проведения громоздких преобразований и других рутинных операций. Не всегда могут оказаться под рукой таблицы преобразований Лапласа.

Во всех ситуациях при наличии компьютера и системы MatLAB для расчета переходных процессов операторным методом целесообразно использовать пакет символьной математики.

Для нахождения преобразования Лапласа функции необходимо использовать запись

,

где - символьное выражение функции во временной области.

Давайте получим с помощью технологии пакета символьной математики операторные соотношения на основе преобразования Лапласа для некоторых наиболее часто встречающихся функций.

В таблице 6.1 приведены решения для изображений и оригиналов четырнадцати различных функций при .

Таблица 6.1.

п/п.	Символьные функции преобразования Лапласа.	Операторная форма и оригинал функции.
1	syms alf fi t A a n b w F1=A*laplace(t^0)	F1 = A/s
	f1=ilaplace(F1)	f1 = A
2	F2=laplace(t)	F2 = 1/s^2
	f2=ilaplace(F2)	f2 = t
3	F3=laplace(t^5)/prod([1:5])	F3 = 1/s^6
	f3=ilaplace(F3)	f3 = 1/120*t^5
4	F4=laplace(exp(-a*t))	F4 = 1/(s+a)
	f4=ilaplace(F4)	f4 = exp(-a*t)
5	F5=laplace(t*exp(-a*t))	F5 = 1/(s+a)^2
	f5=ilaplace(F5)	f5= t*exp(-a*t)
6	F6=laplace(1/2*t^2*exp(-a*t))	F6 = 1/(s+a)^3
	f6=ilaplace(F6)	f6 = 1/2*t^2*exp(-a*t)
7	F7=laplace(1/(b-a)*(exp(-a*t)-exp(-b*t))) Fa7=simplify(F7) pretty(Fa7)	F7 = 1/(b-a)*(1/(s+a)-1/(s+b)) Fa7 = 1/(s+a)/(s+b) 1 --------------- (s + a) (s + b)
	f7=ilaplace(F7)	f7 = 1/(b-a)*(exp(-a*t)-exp(-b*t))
8	F8=laplace((1-a*t)*exp(-a*t)) Fa8=simplify(F8)	F8 = 1/(s+a)-a/(s+a)^2 Fa8 = s/(s+a)^2
	8=ilaplace(Fa8)	f8 = (1-a*t)*exp(-a*t)
9	F9=laplace(1/(b-a)*(b*exp(-b*t)- - a*exp(-a*t))) Fa9=simplify(F9) pretty(Fa9)	F9 = 1/(b-a)*(b/(s+b)-a/(s+a)) Fa9 = s/(s+b)/(s+a) s --------------- (s + b) (s + a)
	f9=ilaplace(Fa9)	f9 =1/(b-a)*(b*exp(-b*t)-a*exp(-a*t))
10	F10=laplace(sin(w*t)) Fa10=simplify(F10)	F10 = w/(s^2+w^2) Fa10 = w/(s^2+w^2)
	f10=ilaplace(Fa10)	f10 = w/(w^2)^(1/2)*sin((w^2)^(1/2)*t)
11	F11=laplace(cos(w*t))	F11 = s/(s^2+w^2)
	f11=ilaplace(F11)	f11 =cos((w^2)^(1/2)*t)
12	F12=laplace(exp(-a*t)*sin(w*t+0.1))	F12 = ((s+a)*sin(1/10)+ + w*cos(1/10))/((s+a)^2+w^2)
	f12=ilaplace(F12) fa12=simplify(f12)	f12 = exp(-a*t)*cos(1/10)*sin(w*t)+ +exp(-a*t)*sin(1/10)*cos(w*t) fa12 = exp(-a*t)*cos(1/10)*sin(w*t)+ +exp(-a*t)*sin(1/10)*cos(w*t)
13	F13=laplace(cosh(a*t))	F13 = s/(s^2-a^2)
	f13=ilaplace(F13)	f13 =cos((-a^2)^(1/2)*t)
14	F14=laplace(1/sqrt(pi*t))	F14 = 1/s^(1/2)
	f14=ilaplace(F14)	f14 = 1/(pi*t)^(1/2)

В первом столбце таблицы указан порядковый номер функции. Во втором столбце содержится оператор syms, который используется для объявления символьных величин. Изображения получаются с помощью функции laplace, а переход от изображений к оригиналам осуществляется посредством ilaplace. Результаты вычислений, выполненных в среде MatLAB, представлены в соответствующих строках третьего столбца таблицы. Кроме функций перехода от оригиналов к изображениям и обратно, в некоторых позициях использованы simplify, pretty и другие операторы, о назначении которых упоминалось ранее. Результаты выполненных преобразований с помощью этих функций также представлены в соответствующих строках третьего столбца. Например, под порядковым номером 9 (первый столбец) следует функция

,

которая, согласно синтаксису оператора laplace, записана в круглых скобках искомого изображения F9 (второй столбец)

.

Компьютерный вариант преобразования F9 представлен в этой же строке (третий столбец):

.

Чтобы упростить эти выражения, введена функция Fa9 (второй столбец):

Результат упрощений приведен в той же строке (третий столбец):

Наконец, применение функции pretty (второй столбец):

позволило получить (см. третий столбец):

.

Функции, служащие для обеспечения инверсного перехода от изображений к оригиналам, в каждой позиции отделены штрих- пунктирной линией.

Для порядкового номера 9, в частности, обратное преобразование, обозначенное функцией , определяется следующим образом (второй столбец):

.

Результат преобразования – исходная функция во временной области (см. третий столбец):

,

что свидетельствует о корректности преобразований.

Решение дифференциальных уравнений требует получения операторной формы для производных от функции. Выполняя преобразование Лапласа, применим операцию интегрирования по частям к производной

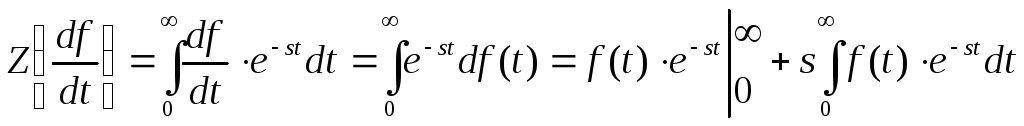(6.11)

Обратим внимание на то, что второе слагаемое представляет собой произведение преобразованной по Лапласу самой функции на оператор . Следовательно, с учетом граничных условий, мы получим:

.

Используем полученное выражение для записи напряжения на индуктивности в операторной форме при ненулевом начальном токе. Предположим, что

,

Тогда, вследствие линейных свойств преобразования Лапласа, будем иметь:

,

где - начальный ток, - индуктивность.

.

Аналогично можно записать ток через емкость в операторной форме. Введем обозначения текущих значений тока и напряжения в операторной форме через знак соответствия:

, .

Предположим, что в момент начальное напряжение на емкости . Ток через емкость равен:

.

В операторной форме

Полученное выражение является алгебраическим. Поэтому

.

Если , то операторная форма записи упрощается:

.

Поскольку

,

а напряжение на конденсаторе во временной области

,

мы можем записать изображение интеграла:

.

Таким образом, интегрирование функции во временной области соответствует в частотной области (в области изображений) делению ее на оператор .

Процедуру получения преобразования Лапласа для производной от функции (6.11) можно распространить на вторую, третью и высшие производные. Например, для второй производной справедливо следующее преобразование:

, (6.12)

где - операторная форма записи самой функции, - значение функции в момент , - значение производной в начальный момент.

Если обозначить -ю производную функции в момент времени как величину

,

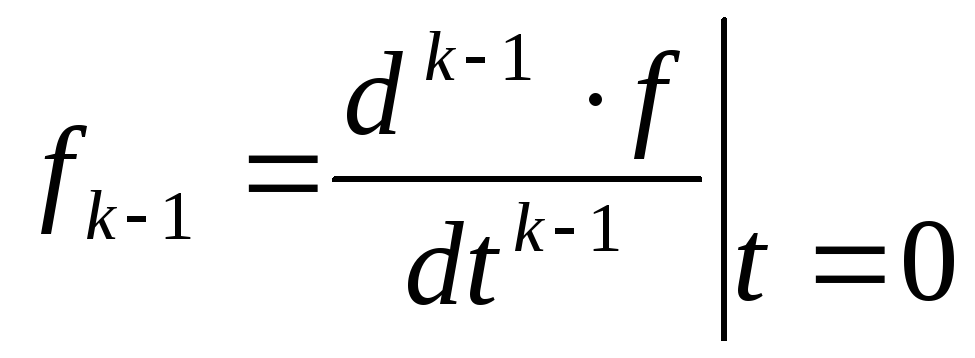то для производной любого порядка можно получить преобразование Лапласа с учетом начальных условий по следующей формуле:

(6.13)

В частности, если , то

,

т.е. получаем вновь выражение (6.12)

Применим изложенные выше положения для моделирования переходных процессов в электрических цепях.

Сначала рассчитаем переходный процесс в разветвленной электрической цепи с одним накопителем энергии. Рассмотрим, например, RL-цепь, изображенную на рис. 6.10. Определим в переходном режиме операторным методом.

Рис. 6.10. Разветвленная цепь

Дифференциальное уравнение цепи

, (6.14)

где и - постоянные коэффициенты.

Ток в момент замыкания ключа К равен

,

ЭДС .

Получим преобразование Лапласа для уравнения (6.14) путем умножения левой и правой частей уравнения (6.14) на экспоненту и приравняв интегралы, согласно

(6.10):

.

Приведенное равенство запишем с помощью знака преобразования:

или, с учетом свойств линейности,

(6.15)

Первое слагаемое в левой части уравнения (4.6-6) при

Правая часть (6.15), где находится постоянная ЭДС, равна (см. таблицу 6.1, функцию 1):

,

и уравнение (6.14) в операторной форме принимает вид:

. (6.16)

Ток играет роль «внутреннего» источника электроэнергии. Уравнение (6.16) – алгебраическое. Его следует решить относительно искомого тока в операторной форме:

(6.17)

Воспользуемся для перехода к оригиналу функцией в пакете символьной математики.

Приведем решение, выполненное на компьютере в режиме прямых вычислений:

>> syms a b E I0 s

>> Iind=ilaplace(b*E/(s*(s+a))+I0/(s+a))

Iind =

b*E/a*(1-exp(-a*t))+I0*exp(-a*t)

>>

Видно, что ток через индуктивность в переходном процессе

Подставляя коэффициенты , и ток в эту формулу, мы получим решение в окончательном виде:

.

Ранее были приведены примеры составления дифференциальных уравнений для описания переходных процессов в RLC – цепях. Записанные в матричной форме, уравнения очень просто преобразуются к операторному виду. Производные от основных переменных состояния в этих уравнениях вынесены в левую часть, и для операторной записи требуется только информация о начальных условиях основных переменных состояния. В правой части уравнений необходимо лишь найти преобразованную по Лапласу ЭДС источника электроэнергии. При наличии в RLC-цепи одного источника модель может быть представлена дифференциальным уравнением

(6.18)

В общем случае начальные условия не равны нулю, т.е.

.

Если , , , операторная запись уравнения (6.18) имеет вид:

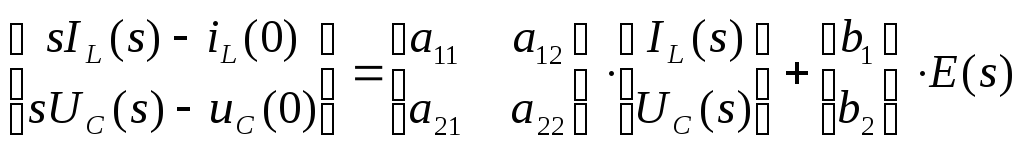
Полученное уравнение является алгебраическим, и поэтому его можно записать:

,

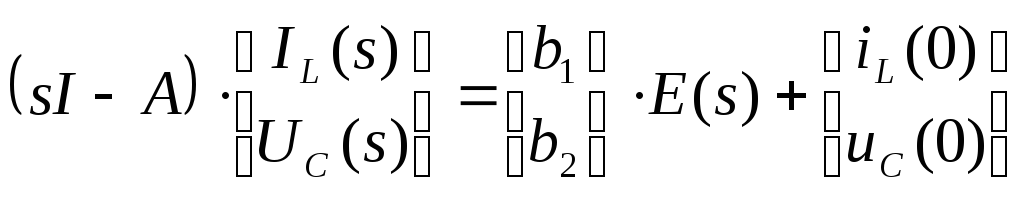где - единичная матрица, - матрица состояния. Решение относительно вектора переменных состояния

(6.19)

Рассмотрим, как следует решать (6.19) с применением пакета символьной математики на примере электрической цепи (рис. 6.11), модель которой соответствует двум дифференциальным уравнениям (6.9):

(6.20)

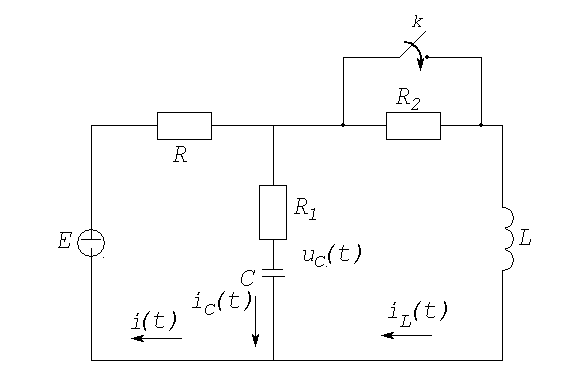
Рис. 6.11. Разветвленная RLC-цепь

, , , , , ,

. ЭДС источника питания . С учетом физических параметров цепи, (6.19) представляется двумя алгебраическими уравнениями:

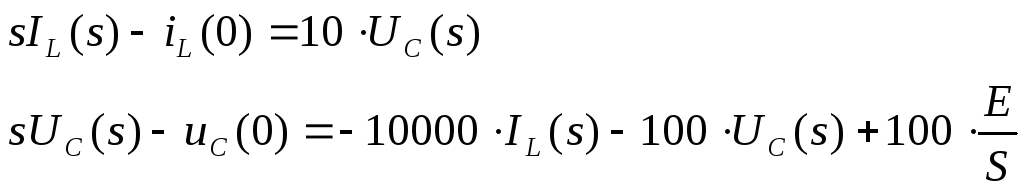(6.21)

где - операторная форма записи постоянной ЭДС, т.е. (см. таблицу 6.1). Конечно, решение (6.21) относительно и никаких трудностей не вызывает. Однако, если число переменных состояния более десятка, лучше обратиться к техническим приемам, позволяющим исключить эту рутинную работу. Ранее мы использовали для этой цели функцию solve пакета символьной математики (см. параграф 6.3). Мы применим функцию для решения рассматриваемой задачи. Для упрощения операций с символьными переменными введем следующие обозначения:

,

Тогда (6.21) можно записать:

,

или, с учетом численных значений ЭДС и начальных условий получим:

,

(6.22)

Система (6.22) полностью подготовлена к решению с помощью функции solve.

Заметим, что объявляемыми символьными переменными должны быть , и . Ниже приводится решение задачи операторным методом в режиме прямых вычислений.

>> syms x y s

>> Z=solve(s*x-10*y-0.1,10000*x+s*y+100*y-3000/s-20);

>> I=Z.x

I =

1/10*(s^2+2100*s+300000)/s/(100000+s^2+100*s)

>> U=Z.y

U =

20*(s+100)/(100000+s^2+100*s)

>> I=ilaplace(I)

I =

3/10-1/5*exp(-50*t)*cos(50*39^(1/2)*t)+19/195*exp(-50*t)*39^(1/2)*sin(50*39^(1/2)*t)

>> U=ilaplace(U)

U =

20/39*exp(-50*t)*39^(1/2)*sin(50*39^(1/2)*t)+20*exp(-50*t)*cos(50*39^(1/2)*t)

>> pretty(I)

1/2 19 1/2 1/2

3/10 - 1/5 exp(-50 t) cos(50 39 t) + --- exp(-50 t) 39 sin(50 39 t)

195

>> pretty(U)

20 1/2 1/2 1/2

-- exp(-50 t) 39 sin(50 39 t) + 20 exp(-50 t) cos(50 39 t)

39

>>

Операторная форма и используется для перехода из области изображений в область оригиналов, осуществляемого функцией инверсного преобразования ilaplace. Функция упрощения pretty позволяет записать:

,

.

Этот результат получен для и , если собственные значения матрицы состояния равны и .

Заметим, что результат моделирования аналогичен ранее полученному решению во временной области (см. рис.6.9).