2.4. Модель многоузлового разветвления русла в стационарном режиме. Аналогии с электрической цепью

Выполнение дноуглубительных работ и планирование мероприятий по улучшению судоходных условий на реках определяют необходимость оценки расходов воды в многоузловых разветвлениях и отметок уровня воды в узлах расчетным путем [33].

Оценки могут быть многовариантными, относящимися к различным полным расходам воды в реке и варьируемым модулям сопротивления рукавов [30].

Использование математической модели многоузлового разветвления русла для выполнения расчетов рабочих параметров может существенно ускорить процесс поиска эффективных решений по поддержанию габаритных глубин на отдельных участках водного пути.

При этом возможно совершенствование методов планирования дноуглубительных работ на реках, поскольку эффект влияния той или иной работы на изменение глубины судового хода может быть оценен по модели, без существенных материальных затрат [32].

Для расчета распределения расхода воды по рукавам разветвления реки допустимо использование статических моделей, рассмотренных подробно в «Руководстве по улучшению судоходных условий на свободных реках» (ЛИВТ, СПб., 1992, с. 54141) и рекомендованных для практического использования в линейных организациях водных путей [38].

Модели многоузловых разветвлений является нелинейным [14], [15]. Они характеризуются высокой чувствительностью к вариации параметров. Поэтому решение задачи и получение количественных оценок рабочих параметров должно базироваться на использовании эффективных вычислительных процедур, обеспечивающих высокую скорость сходимости итерационных процессов.

Чтобы расчет многоузловых разветвлений стал «рабочим инструментом» при планировании и выполнении путевых работ, предлагается вычислительный алгоритм, обеспечивающий жесткое (робастное) решение этой задачи.

Предположим, что нам необходимо рассчитать многорукавное многоузловое разветвление, имеющее узлов и рукавов. Для каждого рукава предварительно рассчитаем модули сопротивлений, которые зададим в форме таблицы. Предположим также, что задан полный расход воды в реке. В общем случае может быть задана отметка уровня воды в нижнем (замыкающем) узле. В случае «ответвлений» расходов – учтем их значения и определим расход на выходе из многоузлового разветвления.

Расход в -ом рукаве связан с отметками свободной поверхности на его концах и с помощью нелинейного уравнения, имеющего вид:

, (2.0)

где ; – модуль сопротивления -го рукава, – постоянное число (показатель степени). В свою очередь, модуль сопротивления является нелинейной функцией длины отдельных участков -го рукава, площадей их живого сечения, глубин, коэффициента шероховатости и др.

Уравнения вида (2.29), по существу, являются уравнениями движения, где – падение свободной поверхности в -ом рукаве.

Рассмотрим теперь -ый узел, к которому по рукавам подводится вода, а по – отводится. Сумма расходов в узле равна нулю, т.е.

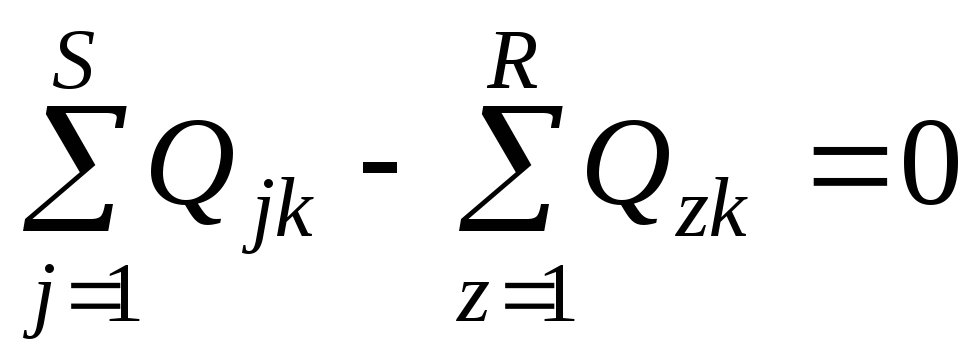(2.0)

Это есть уравнение неразрывности, свидетельствующее о том, что каков объем воды в единицу времени подтекает к узлу, тот же и оттекает от узла, т.е. узел не является буфером (накопителем).

Обычно показатель степени в уравнении (2.29) принимается равным 2. Мы можем допустить иные значения (положительные, большие единицы), что позволяет считать эту функцию строго вогнутой.

Итак, задача формулируется следующим образом: при заданном значении полного расхода воды в реке, известных и , определить и для всех путем совместного решения уравнений (2.29) и (2.30).

Аналогии с электрической цепью

Составим расчетную схему многорукавного многоузлового разветвления любой топологии (конфигурации). Заметим, что на схеме образуются замкнутые контуры, состоящие из соединений отдельных рукавов, и выделены узлы. Если мы вычислим сумму падений свободных поверхностей по любому замкнутому контуру, то она будет равна нулю (узел, из которого мы «выходим» и в который вновь «возвращаемся», следуя по замкнутому контуру, один и тот же). Таким образом, каждый рукав, обладающий соответствующим модулем сопротивления, является аналогом ветви в электрической цепи, активное сопротивление которой численно равно этому модулю. Расход есть аналог тока в -ой ветви, а величина аналогична падению напряжения на -ой ветви. Что касается «отметок» уровней в узлах разветвления, то эти понятия эквивалентны потенциалам узлов.

Если расчетная схема разветвления реки содержит узлов и независимых контуров, то число уравнений, подлежащих решению, равно .

Уравнение (2.30) аналогично первому закону Кирхгофа для электрической цепи, согласно которому алгебраическая сумма токов, подтекающих к любому узлу схемы, равна нулю.

На основе уравнений (2.29) для каждого замкнутого независимого контура (т.е. контура, в состав которого входит хотя бы один рукав, не входивший ранее ни в один из других контуров) можно составить уравнение вида:

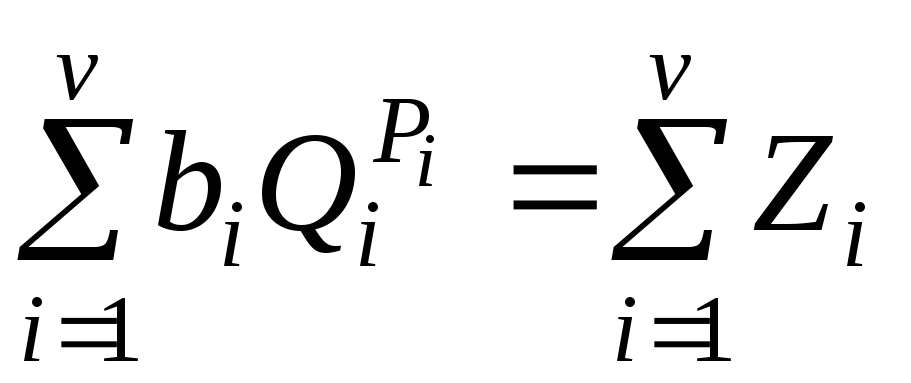, (2.0)

где – число рукавов, входящих в контур. Уравнение (2.31) аналогично второму закону Кирхгофа в электрической цепи, согласно которому алгебраическая сумма напряжений вдоль любого замкнутого контура равна нулю, т.е.

, (2.0)

что справедливо для контура, не содержащего источников ЭДС.

Метод аналогий позволяет применить любой из известных методов расчета электрических цепей непосредственно для расчета многоузловых разветвлений рек и других сетей. В результате расширяется арсенал методов, которыми можно воспользоваться при выполнении инженерных расчетов русловых процессов, т.к. эффективность этих методов всесторонне апробирована в теории электрических цепей и систем.

Необходимо подчеркнуть, что несмотря на кажущуюся простоту уравнений (2.302.32), их решение представляет собой непростую задачу.

Аналог электрической цепи состоит из нелинейных сопротивлений, и ее расчет требует особого подхода, который базируется на следующем алгоритме.

Алгоритм расчета многоузлового разветвления русла

Уравнения (2.30) и (2.32) можно записать в векторно-матричной форме. Общий вид уравнения

, (2.0)

где – вектор искомых переменных.

Зададимся нулевым приближением

(2.0)

Тогда вектор погрешностей на нулевой итерации равен:

(2.0)

Согласно вычислительной процедуре Ньютона-Рафсона-Канторовича, решение на первом шаге:

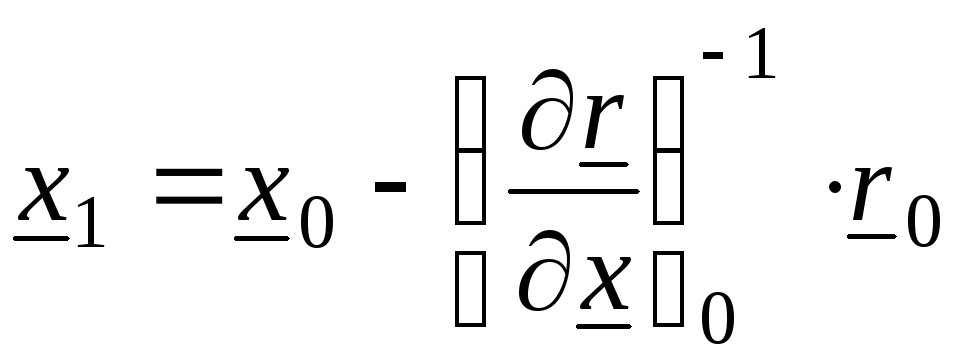, (2.0)

где матрица

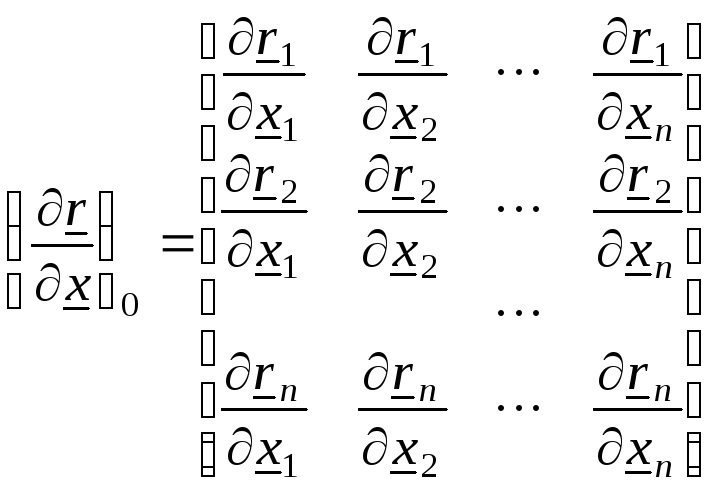(2.0)

есть матрица, называемая Якобианом.

В общем случае формула Ньютона-Рафсона-Канторовича для вектора состояния на -ой итерации имеет вид:

(2.0)

По формуле (2.38) выполняются вычисления до момента, соответствующего сходимости решения. Сходимость гарантируется строго вогнутым характером нелинейности, определяемым показателем степени в уравнениях вида (2.31)

Обычно число итераций не превышает 34 при сходимости решения до 5-го знака после запятой.

Пример расчета многорукавного многоузлового разветвления

русла реки

Рассмотрим расчетную схему многорукавного многоузлового разветвления, представленную на рис. 2.8 [38].

Разветвление состоит из семи ветвей и шести узлов, обозначенных на рисунке соответствующими числами. Приток к первому узлу равен . Он представляет собой полный расход воды в реке. Отток от первого узла (узел 1) осуществляется по рукавам 1 и 2. Модуль сопротивления первого рукава , а второго, соответственно, . Расходы в рукавах обозначены индексами и , а направления потоков воды указаны стрелками.

В о втором и пятом узлах производятся ответвления по каналам (сброс воды) с расходами и . Эти величины приняты постоянными. Без потери общности они могут быть функциями отметок соответствующих узлов, либо других переменных состояния разветвления.

Согласно расчетной схеме, основной отток воды происходит от шестого узла и равен . Нетрудно видеть, что .

Аналогично первому узлу, на схеме введены обозначения расходов и модулей сопротивлений всех ветвей, а также обозначения отметок высот всех узлов [38]. Отметка (обычно принимаемая в электрической цепи в качестве нулевого потенциала) при выполнении расчета принята равной (м).

Предполагается, что модули сопротивлений рукавов вычислены по существующим методикам и равны: , , , , , , , где – коэффициент , обеспечивающий размерность каждого , равную .

В уравнениях движения (2.29) для всех рукавов показатели степени приняты , т.е. падение свободной поверхности в каждом рукаве пропорционально квадрату расхода. В общем случае это условие может быть иным.

Как было отмечено выше, решение нелинейной задачи связано с выполнением достаточно громоздкой вычислительной процедуры. Поэтому, по возможности, на стадии постановки задачи необходимо придерживаться принципа уменьшения числа переменных [10]. Иначе говоря, размерность задачи целесообразно выбрать минимальной. В этой связи простой анализ расчетной схемы, представленной на рис. 2.8, позволяет выразить расход в третьей ветви, расположенной между узами 2 и3 (модуль сопротивления ), в терминах расхода :

,

а в седьмой ветви, расположенной между узлами 5 и 6 (модуль сопротивлений ), в терминах :

.

Задача будет решена, если мы определим расходы , , , и (см. рис. 2.8). С этой целью необходимо составить пять уравнений с пятью неизвестными.

Учитывая возможность сокращения числа переменных, мы можем исключить из рассмотрения узлы 2 и 5. Тогда при составлении уравнений неразрывности мы должны учитывать расходы только в рукавах, сходящихся к узлам 1, 3, 4 и 6. Эти узлы обозначены буквами A, B,C и D.

Согласно первому закону Кирхгофа, для цепи с четырьмя узлами возможно составить три уравнения неразрывности.

Для узла А:

, (2.0)

для узла B:

, (2.0)

для узла С:

(2.0)

Два (недостающих до пяти) уравнения получим с помощью второго закона Кирхгофа. С этой целью составим уравнения для свободных поверхностей в двух контурах. Первый контур (обозначен на схеме цифрой I) состоит из ветвей с модулями , , , , и . Во второй контур входят ветви с модулями , , и (на схеме обозначены цифрой II). При составлении уравнений контуры будем обходить по часовой стрелке.

(2.0)

Аналогично для второго контура будем иметь:

(2.0)

Согласно алгоритму, изложенному выше, решим нелинейную систему уравнений (2.392.43), используя вычислительную процедуру Ньютона-Рафсона-Канторовича. С этой целью введем функции:

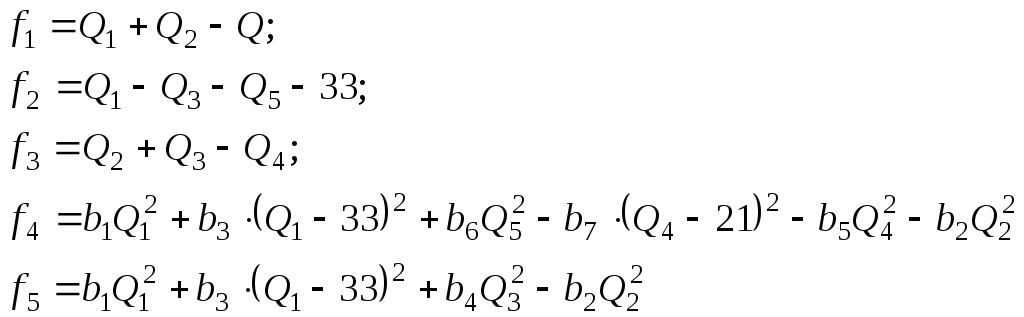(2.0)

Из (2.44) образуем вектор-столбец:

, (2.0)

где знак «;» в среде MatLAB является знаком разделения столбцов. Введем вектор переменных состояния:

, (2.0)

где – знак транспонирования.

Согласно (2.38) определим Якобиан. Для (2.45) Якобиан имеет вид:

, (2.0)

где ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; .

Затем, используя формулу (2.36), мы получим:

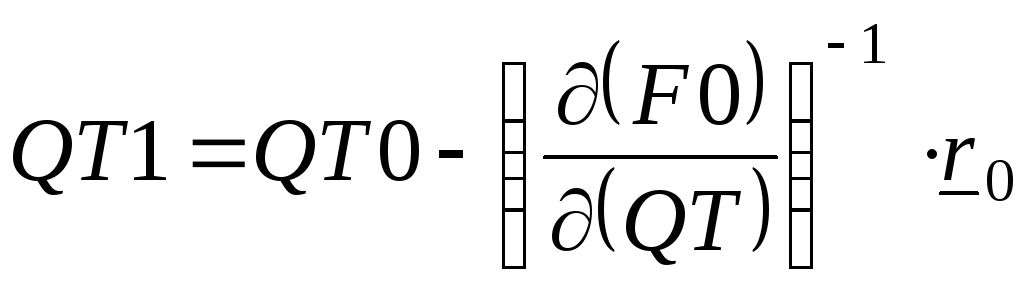, (2.0)

где , вычисляемое с помощью (2.45) путем подстановки нулевого приближения.

Последующие вычисления выполняются по уравнению (2.38) рекуррентно. Заметим, что на каждом шаге (итерации), согласно (2.38) и (2.48) необходимо определить инверсную матрицу размерности (55). Для нахождения расходов во всех рукавах можно ввести вектор-столбец размерности (71):

.

Предположим, что полный расход Q = 819 м³/с.

Зададимся произвольно нулевым решением:

.

Тогда расходы в рукавах на первом шаге (первое приближение), определяемые по формуле (2.48), будут равны:

.

На пятой итерации решение данной задачи сходится с погрешностью, не превышающей шестого знака после запятой. В результате:

.

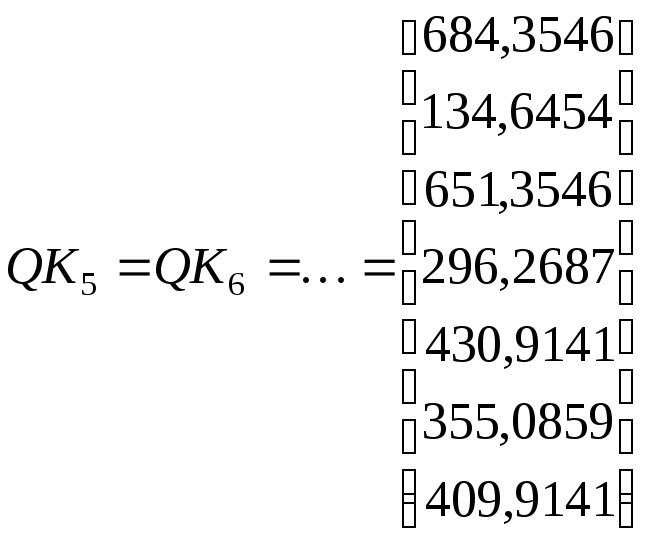Вектор отметок уровней в 16 узлах схемы:

.

Поскольку сходимость решения при любом выбранном нулевом приближении обеспечивается за четыре итерации, в процессе вычислений на ЭВМ был выбран цикл, обеспечивающий «сборку» результатов вычислений на шестой итерации, и произведены расчеты отметок уровней узлов и расходов в рукавах при изменении расходов реки от 800 до 1800 (м³/с) с шагом дискретности (м³/с).

По результатам расчетов построены графики, приведенные на рис. 2.9 и рис. 2.10. Цифрами на рисунках отмечены номера узлов и рукавов разветвления, к которым относятся соответствующие кривые.

Программа для расчета многоузлового разветвления русла

Полный текст программы для расчета расходов и отметок уровней в узлах разветвления русла приведен в файле .

Расчет выполняется с помощью двойного цикла, заданного операторами и . Каждый внутренний цикл, реализующий процедуру Ньютона-Рафсона-Канторовича, выполняется за шесть итераций .

Вычисления во внешнем цикле предусматривают получение значений отметок уровней в узлах и расходов в рукавах при вариации полного расхода реки в пределах 8001800 (м³/с) с шагом дискретности 10 (м³/с).

Расчет завершается формированием матрицы уровней размерности (6101) и расходов – (7101).

По полученным данным построены графики уровней и расходов рукавов. Нумерация функциональных зависимостей на рисунках 2.9 и 2.10 соответствует обозначениям, введенным на расчетной схеме разветвления русла реки.

Время вычислений на компьютере с тактовой частотой процессора 66 (мГц) составляет 16 (с).

Файл

% Модель многоузловаого разветвления при известном наполнении русла.

% Файл "Sah122.m".

clc

% Вектор уровней YRW, вектор расходов RSX.

YRW=[]; RSX=[];

% Вариация полного расхода воды в реке от 800 куб. м./с до 1800 куб. м./с с шагом

% дискретности 10 куб. м./с

for Q=800:10:1800;

% Нулевое приближение. Элементы вектора QTZ (расходы воды в рукавах Q1?Q7)

% выбираются произвольно. Например,

Q1=100; Q2=100; Q3=100; Q4=100; Q5=100; Q6=100; Q7=100;

% Отметка уровня воды в нижнем замыкающем узле (в метрах):

z6=3.544;

% Постоянный коэффициент, входящий в выражение модуля сопротивления рукавов:

k=1.0E-08;

% Модули сопротивления рукавов (размерностьC^2/M^5):

b1=4.61*k; b2=431.5*k; b3=5.67*k; b4=37.12*k; b5=12.8*k; b6=160.1*k; b7=86.6*k;

%=================================================================

% Формирование векторов расходов:

QT=[Q1 Q2 Q4 Q5 Q6]';

QTZ=[Q1 Q2 Q3 Q4 Q5 Q6 Q7]';

% Метод Ньютона-Рафсона-Канторовича. Число итераций I=6:

Pacx=[];

YPOVH=[];

for I=1:6;

% Составление уравнений по 1-ому и 2-ому законам Кирхгофа:

f1=QT(1)+QT(2)-Q;

f2=QT(1)-QT(3)-QT(5)-33;

f3=QT(2)+QT(3)-QT(4);

f4=(QT(1).^2).*b1+((QT(1)-33).^2)*b3+(QT(5).^2).*b6-(QT(2).^2).*b2-(QT(4).^2).*b5-((QT(4)-21).^2).*b7;

f5=(QT(1).^2).*b1+((QT(1)-33).^2).*b3+(QT(3).^2).*b4-(QT(2).^2).*b2;

% Вектор-функция f:

f=[f1; f2; f3; f4; f5];

% Матрица Якоби:

D=[1 1 0 0 0; 1 0 -1 0 -1; 0 1 1 -1 0; QT(1).*2.*b1+(QT(1).*2-66).*b3, -QT(2).*2.*b2, 0, -QT(4).*2.*b5-(QT(4).*2-42).*b7, QT(5).*2.*b6; QT(1).*2.*b1+(QT(1).*2-66).*b3, -QT(2).*2.*b2, QT(3).*2.*b4, 0, 0];

% Вектор расходов на предшествующем шаге:

X0=[QT(1) QT(2) QT(3) QT(4) QT(5)]';

% Вектор расходов на последующем шаге:

X1=X0-(inv(D))*f;

% То же для семи рукавов:

QK=[X1(1), X1(2), X1(1)-33, X1(3), X1(4), X1(5), X1(4)-21]';

% Расчет отметок уровней в узлах:

z3=z6+(QK(6).^2).*b6;

z5=z6+(QK(7).^2).*b7;

z4=z5+(QK(5).^2).*b5;

z2=z3+(QK(3).^2).*b3;

z1=z2+(QK(1).^2).*b1;

zp1=z4+(QK(2).^2).*b2;

% Вектор уровней:

ZK=[z1 z2 z3 z4 z5 z6]';

QT=X1;

Pacx=[Pacx, QK];

YPOVH=[YPOVH, ZK];

end,

PACXOD=[QTZ, Pacx];

YRW=[YRW YPOVH(:,6)];

RSX=[RSX PACXOD(:,7)];

end,

YRW;

RSX;

% Построение графиков:

st=800:10:1800;

plot(st, YRW, 'r'), grid

% text(700, 5, 'H(m)')

text(1350, 4.25, '1')

text(1700, 4.5, '2')

text(1615, 4.3, '3')

text(1650, 4.2, '4')

text(1730, 4.16, '5')

text(1400, 3.55, '6')

% text(810, 2.8, ' 2.')% Отметки свободной поверхности в узлах разветвления реки.')

% text(1700, 3.2, 'Q(m^3/c)')

pause,

plot(st, RSX, 'g'), grid

text(1400, 1180, '1')

text(1500, 1180, '3')

text(1380, 730, '5')

text(1480, 700, '7')

text(1600, 650, '6')

text(1600, 500, '4')

text(1500, 250, '2')

pause