1.9. Алгоритм ортогонализации в оценке параметров динамических систем

В процессе управления сложными нелинейными системами необходимо решать задачу совместного оценивания параметров и вектора переменных состояния по результатам измерений. Эффективность и качество реализации процедуры оценивания во многом зависят от выбранной модели, технологии обработки экспериментальных данных и измерений зашумленных сигналов. Традиционно для описания нелинейных объектов и оценивания их параметров используются ряды Вольтерра, а для оценки по конечному числу наблюдений – обобщенные регрессионные модели, Марковские оценки, фильтры Винера, Калмана-Бьюси в различных модификациях и др. К сожалению, модели функциональных рядов, используемые для аппроксимации нелинейных объектов, в большинстве практических ситуаций связаны с решением задач высокой размерности, что доставляет определенные неудобства. Если будущие значения переменных состояния зависят от поведения системы в прошлом и изменяющегося во времени входного сигнала, то для аналитического описания нелинейных динамических систем при наличии шума может успешно использоваться класс нелинейных авторегрессионных моделей со скользящим средним (модели NARMAX). Этот класс моделей позволяет обеспечить высокую степень адекватности в поведении модели и объекта при сохранении довольно низкой (как правило, – не превышающей десяти аддитивных составляющих) размерности модели. Однако, если составляющие шума, воздействующего на вектор входного сигнала, коррелированы, то качество моделирования заметно снижается, и требуется предпринимать меры по совершенствованию алгоритма оценивания.

Задача может быть решена с помощью предлагаемого алгоритма, базирующегося на процедуре ортогонализации, реализуемой с помощью верхней треугольной и диагональной матриц, обеспечивающих оценки коэффициентов модели и исключающих влияние последующих коэффициентов на предыдущие. Алгоритм основан на использовании модели NARMAX с ортогональными свойствами.

Рассмотрим нелинейную дискретную модель системы

, (1.68)

где y(t) – выходной сигнал, u(t) – управление, - сигнал ошибки , , - целые числа, соответствующие транспортному запаздыванию (лагу), вводимому по каждой переменной и группам переменных при выборе структуры модели. Если нелинейная функция f, отражающая специфику поведения системы в динамике, может быть аппроксимирована полиномом, то, ограничиваясь составляющей модели, линейной относительно оцениваемых параметров, для случая мы можем представить NARMAX – модель (1.68) в следующем виде

(1.69)

Тогда путем введения обозначений

, , , , ,

для N измерений, превышающих число оцениваемых параметров, мы можем получить переопределенную систему уравнений в матричной форме

, (1.70)

где матрица H, содержащая данные измерений, состоит из элементов

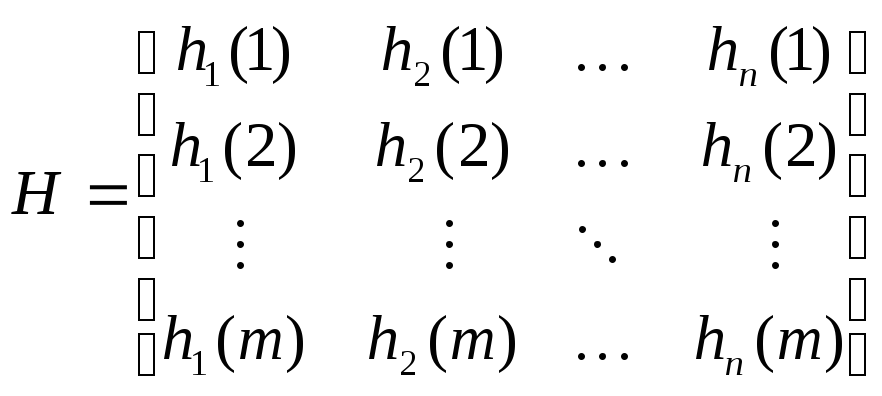, H - -матрица, ,

где n – число оцениваемых параметров. Вектор выхода

,

вектор оцениваемых параметров

и вектор ошибок

.

Вектор параметров можно оценить с помощью операции псевдоинверсии Мура-Пенроуза, либо методом наименьших квадратов. В частности, согласно МНК, наилучшая оценка , реализованная путем решения матричного уравнения

(1.71)

позволяет получить минимум критерия качества

.

Известно, что для распределения ошибки обеспечивается несмещенная оценка вектора параметров модели (1.70). В случае плохо обусловленной корреляционной матрицы , для оценки используются -разложение, -преобразование, либо алгоритм Гивенса. Однако они не обеспечивают оценки каждого параметра в отдельности подобно предложенному алгоритму, базирующемуся на процедуре ортогонализации.

Заметим, что корреляционная матрица , входящая в уравнение (1.71) является симметричной и положительно определенной. Следовательно, возможна ее декомпозиция в форме равенства

, (1.72)

где матрица преобразования - верхняя треугольная, а - диагональная матрица, состоящая только из элементов, больших нуля. Если определена , то путем подстановки в (1.70) единичной матрицы , мы можем получить

, (1.73)

где и . В этом случае нетрудно найти элементы диагонали матрицы , входящей в уравнение (1.72). Действительно, если

, (1.74)

то с учетом операции транспонирования произведения матриц

,

можно (1.74) преобразовать к виду

,

а с учетом равенства (1.72), получить саму матрицу

(1.75)

Теперь остановимся на алгоритме вычисления элементов матриц и . Сначала выберем структуру :

(1.76)

Введем обозначения элементов корреляционной матрицы со свойствами симметрии:

.

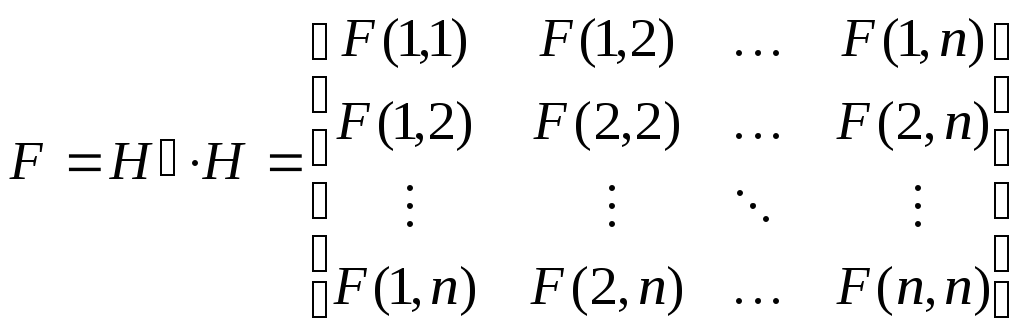Предлагается следующий вычислительный алгоритм для нахождения элементов и :

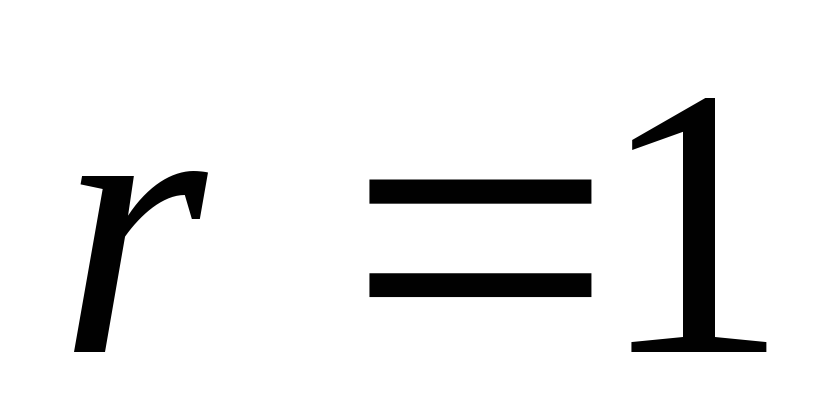1. Если и , коэффициенты первой строк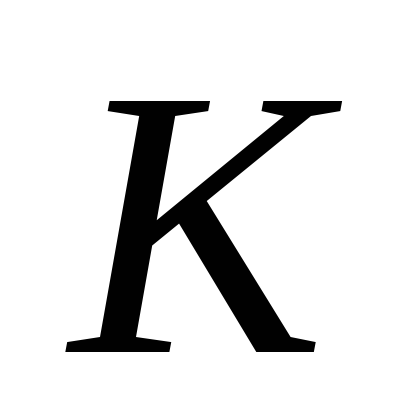и и 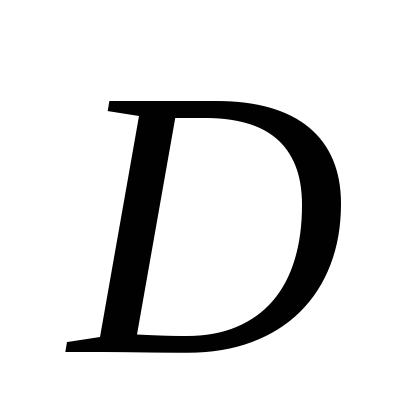рассчитываются с помощью соотношений

, .

2. Для и

.

3. В случае, если 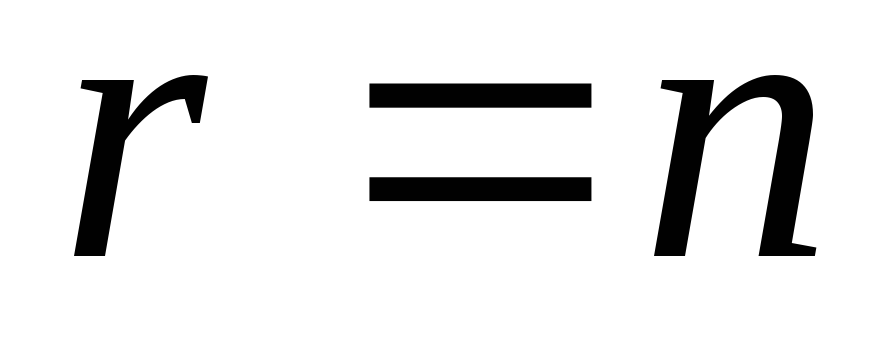, рассчитывается только коэффициент 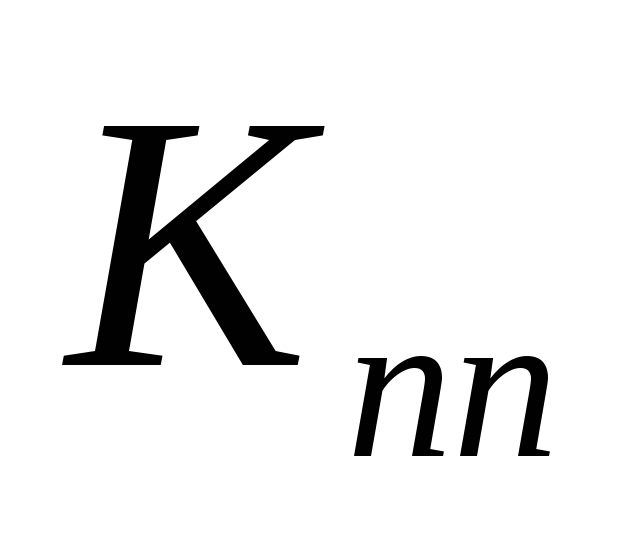по формуле

.

Приведенный вычислительный алгоритм обладает рядом свойств, позволяющих анализировать «внутреннюю» структуру процедуры оценивания параметров модели по результатам измерений. Видно, что для каждого значения коэффициент в модели (1.73) не зависит от других коэффициентов . Поэтому выбор структуры модели и, в частности, назначать размерность можно целенаправленно, с учетом весовой составляющей каждого вводимого коэффициента, вносимой в уменьшение критерия качества. Оценку вектора , с учетом уравнения (1.73), можно получить с помощью соотношения

.

Однако, поскольку. согласно (1.75), , то оценка

,

и после умножения слева на матрицу нетрудно для получить аналитические зависимости, позволяющие привести путем ортогонализации оценки параметров (1.71) при наличии коррелируемого сигнала к эквивалентной последовательности, обладающей свойствами белого шума. Среднее значение

,

и, следовательно, для в виде белого шума с нулевым математическим ожиданием при отсутствии корреляции на входе модели

,

что свидетельствует о несмещенной оценке . При этом легко вычисляется матрица ковариации оцениваемых параметров:

где использовано соотношение

.

Тогда ковариацию для вектора оцениваемых коэффициентов модели (1.70) можно представить в терминах (1.73):

.

Рассмотрим пример оценки с помощью приведенного алгоритма коэффициентов производственной функции Кобба-Дугласа по статистическим рядам. Эта функция является моделью экстенсивного способа производства, осуществляемого за счет факторов производства – затрат капитала и трудовых затрат . В производственную функцию введем время , что позволит учесть ряд качественных изменений, происходящих в технологических схемах производства. Тогда математическая модель производственной функции принимает вид

, (1.77)

где - объем выпуска продукции, и - постоянные коэффициенты, причем . В модель (1.77) временной фактор введен в виде экспоненциального мультипликатора [24]. Оценку масштабного коэффициента и постоянных коэффициентов и произведем по исходным статистическим рядам, приведенным в работе [24] для внутренней частной экономики США в период с 1947 г. по 1968 г. (см. таблицу 1.3).

Таблица 1.3

Год	Конечный продукт , млрд. долл. (1958 г.)	Основной капитал , млрд. долл. (1958 г.)	Отработанные человеко-часы , млрд.
1947	280,2	204,2	109,3
1948	293,8	212,9	110,0
1949	292,8	196,2	109,1
1950	322,9	227,4	111,3
1951	343,9	239,4	113,9
1952	352,3	244,3	113,8
1953	369,8	264,9	114,9
1954	364,9	248,1	110,8
1955	395,5	282,2	114,8
1956	402,8	295,2	116,5
1957	408,5	298,2	114,3
1958	403,2	269,5	111,1
1959	431,1	300,4	113,7
1960	441,7	303,9	114,1
1961	449,5	302,7	113,8
1962	479,5	317,0	115,5
1963	499,3	329,6	117,5
1964	522,1	351,7	119,3
1965	569,9	388,2	122,2
1966	599,6	441,2	124,0
1967	612,7	447,4	123,6
1968	643,4	472,9	125,2

Уравнение (1.77) можно представить в виде функции, линейно зависящей от оцениваемых параметров и , если вместо данных конечного продукта , основного капитала и отработанных человеко-часов использовать их логарифмы. Тогда, согласно (1.77), получим

или в векторно-матричной форме

,

,

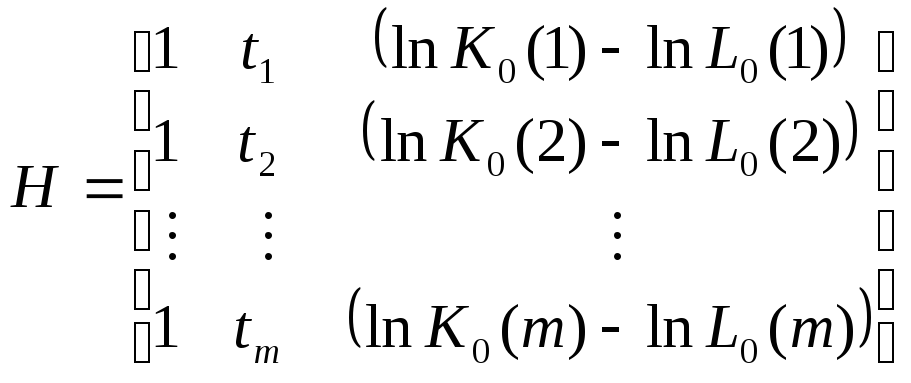где . Максимальное значение определяется данными таблицы 1.3 стохастических рядов (с 1947 г. по 1968 г. включительно).

В результате симметрическая матрица

.

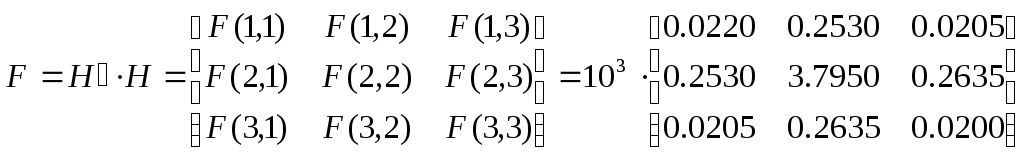Соответственно, коэффициенты матриц ортогональных преобразований и , согласно алгоритму, рассчитываются с помощью соотношений:

, , , , , ,

,

.

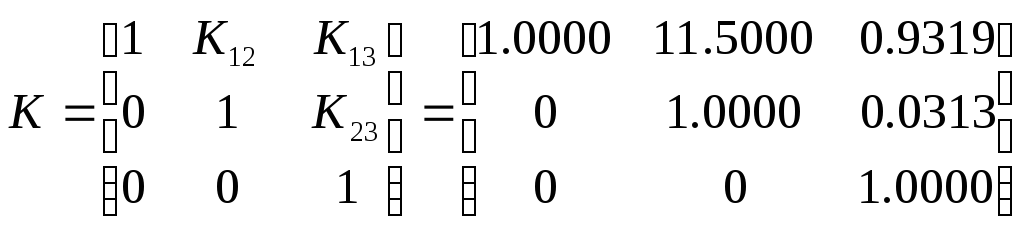Можно убедиться в том, что произведение

,

где , и оценка вектора коэффициентов .

,

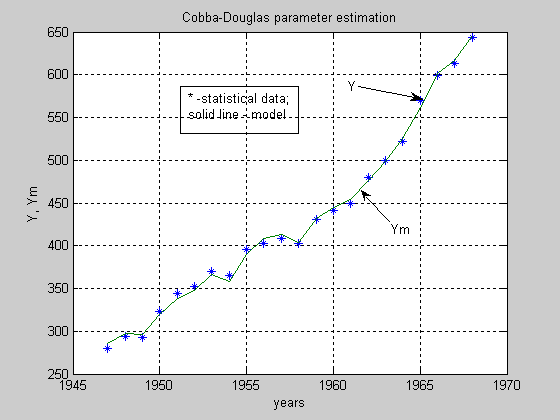
Рис.1.1. Результаты моделирования производственной функции

по оцениваемым коэффициентам

и, наконец, оценка коэффициентов производственной функции Кобба-Дугласа

.

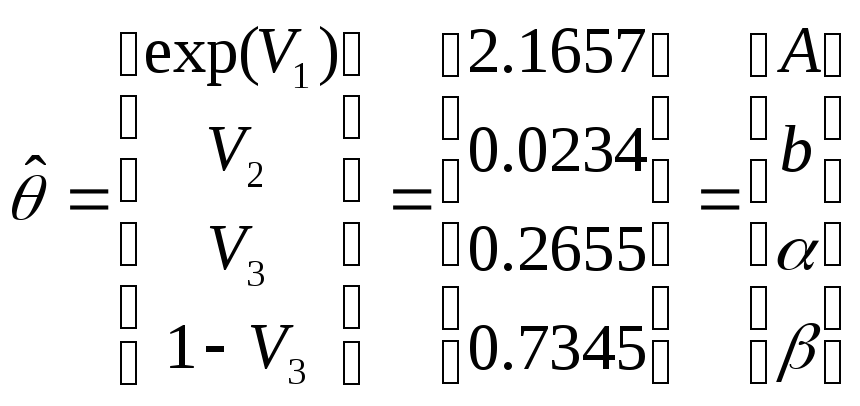Таким образом, модель производственной функции

. (1.78)

На рис. 1.1 представлены расчетные значения производственной функции по модели (1.78) в виде непрерывной характеристики. Данные статистического ряда нанесены на график в виде знаков «*». В заключение отметим, что оценочные значения, произведенные по предложенному алгоритму, идентичны коэффициентам, полученным ранее в работе [10 , с. 42], что подтверждает корректность предложенных решений.