7.2. Программное обеспечение и моделирование нелинейных дискретных систем. Хаос

Представляет большой интерес логистическая модель следующего вида:

N_t+1=N_t(1 + r(1-N_t /K)), t=0, 1, 2, 3, … . (7.11)

Это нелинейная модель. Она относится к очень важному классу динамических систем – к системам с дискретными отображениями. Примером такой дискретной системы, широко используемой для моделирования динамики биологических процессов, а также технологических процессов в технических комплексах различного назначения является система со стробоскопическим наблюдением переменных (отображением Пуанкаре).

В рассматриваемой же ситуации дискретное отображение в форме (7.11) непосредственно определяется природными свойствами экологических процессов динамики популяций.

Динамические свойства дискретной системы (7.11) необходимо исследовать при известных начальных условиях N₀, что не должно вызывать в общем серьезных вычислительных трудностей. Однако, несмотря на кажущуюся простоту, итерационные отображения обладают внутренней (структурной) сложностью, которая определяется параметрами (7.11), в частности, коэффициентами r и К. Этим нелинейным отображениям было посвящено большое число публикаций, в том числе-с совершенно неожиданными результатами. Один из наиболее интересных и показательных результатов состоит в обнаружении свойств универсальности отображений. Универсальность проявляется в переходе от регулярных к хаотическим процессам, осуществляемом по так называемому “сценарию Фейгенбаума”. Предположим, что К=1. Тогда мы можем записать два дискретных квадратных уравнения:

N_t+1 = N_t+ rN_t(1-N_t), t = 0, 1, 2, 3, …, (7.12)

y_t+1=y_t²+c, t=0, 1, 2, 3, … , (7.13)

где с- постоянный коэффициент.

Заметим, что (7.12) и (7.13) идентичны и различаются лишь масштабами переменных состояния. Они описывают один и тот же динамический процесс в экологической системе. Чтобы убедиться в этом, введем обозначения

с =, . (7.14)

Если начальное условие

- r · N₀,

то

- r · N_t, t=1,2,3, …. (7.15)

Произведем подстановку (7.15) в уравнение (7.13). В результате получим

N_t+1 = N_t + r N_t (1-N_t) + K,

где

К = - - .

Приравнивая коэффициент К к нулю, будем иметь

с = ,

при котором

N_t+1 = N_t + r N_t (1-N_t), t = 0, 1, 2, 3, …

полностью совпадает с уравнением (7.12). В теории экологических систем это уравнение нашло широкое применение, начиная с пятидесятых годов еще восемнадцатого века. Бельгийский математик Р.Ф. Бергольц в 1845 г. впервые предложил эту модель для исследования динамики популяций отдельного биологического вида. В настоящее время в моделях используется иная, более удобная форма записи. Ее можно получить из (7.12), если ввести линейное преобразование

, a = 1+r.

После выполнения простых операций формула примет вид

x_t+1 = ax_t(1-x_t), t = 0, 1, 2, 3, … (7.16)

Рассмотрим график, соответствующий уравнению (7.16) и представленный непрерывной функцией

y=ax(1-x)

Это парабола, проходящая через точки (0.0) и (1.0), независимо от заданного параметра а. Максимальное значение y всегда расположено в точке с координатой по оси х=0.5. Ордината точки y=а/4. Парабола y=f(x) является верхней границей для любых процессов, описываемых логистическим уравнением (7.16), где х_t принимает значения на рабочем интеграле 0x_t1, при условии, что х₀ также принадлежит этому интервалу. Теперь для построения итеративного процесса в виде последовательности x₀, x₁, x₂, …на плоскости можно предложить простой графический метод, состоящий в следующем. Построим график параболы y=ax(1-x)  и изобразим на плоскости y=f(x) прямую y=x, разделяющую плоскость пополам и проходящую через точки (0,0), (1,1). Предположим, что начальное условие x₀ 0. Проведем прямую, параллельную оси y и проходящую через x₀ , до пересечения с параболой. Через полученную точку проведем прямую, параллельную оси x , до пересечения с прямой y=x. В результате мы получим абсциссу точки процесса на первой итерации x_t=x₁. Вновь проведем через эту точку прямую, параллельную y, до пересечения с параболой и т.д. В процессе построения траектории все точки на прямой должны располагаться на одинаковом расстоянии от осей y и х.

Основное преимущество графического способа решения логистического уравнения (7.16) состоит в том, что он позволяет наблюдать за рекуррентным процессом и визуально оценивать свойства устойчивости, либо неустойчивости динамики популяций.

Информационная поддержка процесса графического анализа динамики, определяемой уравнением (7.16), обеспечивается файлом sah46.m. Файл состоит из двух основных частей, разделенных штриховыми линиями после задания r. В первой части выполняются построения параболы и прямой, которые используются для генерирования амплитудных значений переменных состояния.

%File "SAH46.M".

%Period-Doubling Bifurcations.

%Iteration of logistic map.

r=0.95;

%---------------------------

x=0:0.01:1;

y1=4*r.*x.*(1-x);

y2=x;

plot(x,y1,x,y2)

hold on,

%---------------------------

x=0.01;

y=0.0;

s=[];

s1=[];

for n=1:500;

s=[s;x;x];

y=4*r.*x.*(1-x);

s1=[s1;x;y];

x=y;

end

plot(s,s1),grid

pause,

hold off

Работа этой части файла завершается соответствующими графическими построениями с использованием оператора hold on, который позволяет сохранить рисунок и продолжить нанесение на него других расчетных зависимостей, получаемых во второй части.

Вторая часть начинается с выбора начального условия х=0.01 (на нулевом шаге). Здесь вводятся «пустые» вектора S и S₁, которые заполняются на каждом шаге цикла, организованного с помощью операторов for, end. По завершении расчетов представляются графики динамических процессов в координатах x_t+1=f(x_t) для различных значений параметра а, который в программе записан в виде равенства а=4r.

Для моделирования процесса с помощью приведенного выше файла требуется задать значения r, х во второй части программы, а затем назначить число шагов t. В представленном варианте файла r=0.95, x=0.01 и число шагов t_max=500.

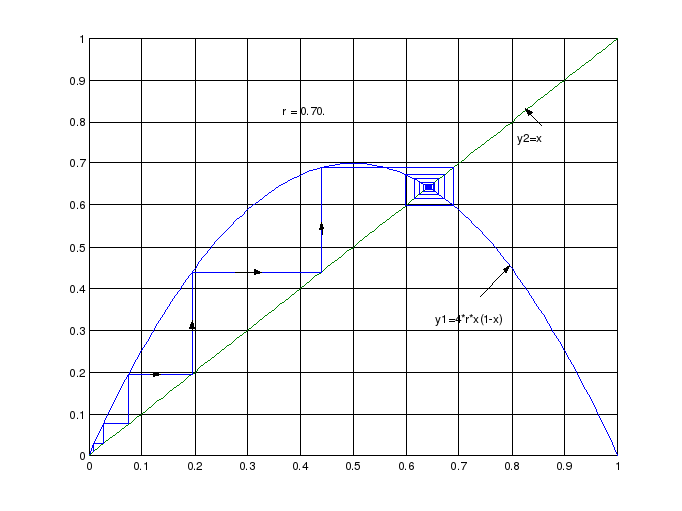
Рис. 7.1. Устойчивый процесс динамики логистической системы

r=0.7, x₀=0.01, f_max=500

Программа завершается оператором hold off, который «отменяет» условие нанесения различных графиков на один рисунок.

Приведем несколько характерных решений, полученных в процессе моделирования с помощью файла sah46.m.

На рис. 7.1 изображен переходный процесс в динамической системе (7.16) при следующих значениях параметров: r=0.7, x₀=0.01. t_max=500.

Стрелками показано направление движения изображающей точки по траектории. Процесс начинается с пошагового движения в направлении точки устойчивого равновесия. На 14-ой итерации переменная состояния достигает значения x₁₄=0.6364, а на 450-ой итерации с точностью до четвертого знака после запятой

x_t=x_t+1=0.6429.

Для представленного на графике процесса характерно

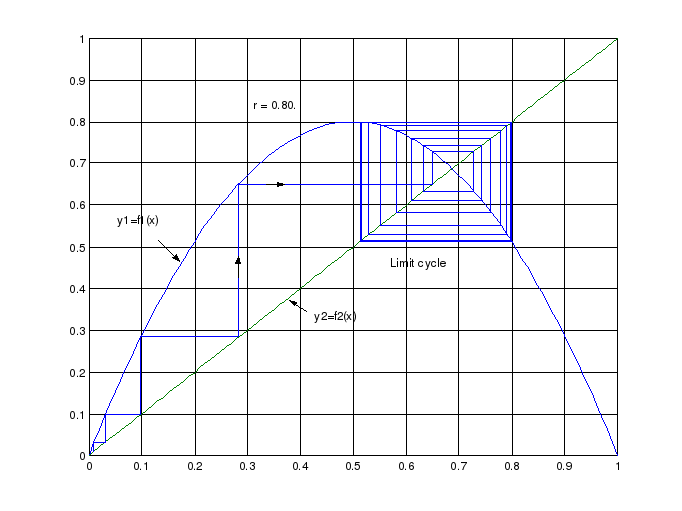
Рис. 7.2. Процесс с устойчивым предельным циклом

r=0.8, x₀=0.01, f_max=500

появление периодических быстро затухающих колебаний в области точки устойчивого равновесия.

Увеличение коэффициента до значения r=0.8 приводит к заметным изменениям динамических свойств системы. Представленный на рис.7.2 переходный процесс (при неизменных начальных условиях) содержит устойчивый предельный цикл, на который изображающая точка переходит “изнутри”, т.е. из области пересечения граничных характеристик.

Необходимо подчеркнуть, что увеличение r в сравнении с предыдущим процессом всего на 0,1 приводит к кардинальным изменениям динамических свойств логистического процесса.

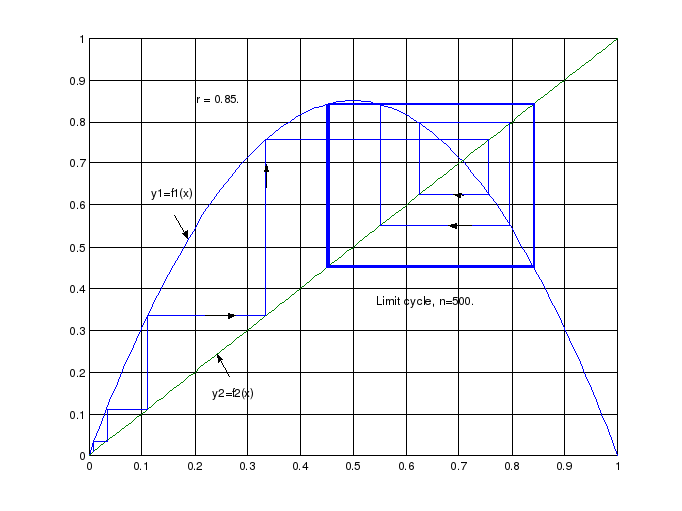
Рис. 7.3. Увеличение амплитуды предельного цикла

r=0.85, x₀=0.01, f_max=500

На следующем рисунке (рис 7.3), содержащем фазовый портрет динамической системы, полученный для r=0.85, можно наблюдать существенные изменения, сводящиеся в основном к увеличению амплитуды устойчивого предельного цикла. Для этого процесса, как и предыдущего, характерен устойчивый периодический режим, который достигается на меньшем числе шагов.

Дальнейшее увеличение параметра системы до величины r=0.90 приводит к возникновению хаоса (рис. 7.4). Если вывести на дисплей вектор S1 (см. файл sah46.m ), то можно убедиться в сложности определения периодичности решений. Это свидетельствует о неравномерных интервалах времени достижения граничных значений переменными состояния. Хаотическое поведение характеризуется крайней степенью неустойчивости движения.

Рис. 7.4. Хаотический процесс

r=0.90, x₀=0.01, f_max=500

Дискретные модели логистических систем не являются тривиальным разностным аналогом соответствующих дифференциальных уравнений, а возникают при изучении заметно синхронизированных процессов [35] . На рис. 7.5 представлен хаотический процесс, полученный в системе, когда r=95. Как и на предшествующем рисунке, мы наблюдаем процесс с возрастающим числом решений (t-периодический процесс с числом периодов, составляющим несколько тысяч), которые чрезвычайно чувстви-тельны к изменению начальных условий и флуктуации параметров модели. Хаотический режим напоминает шумоподобный процесс в системе.

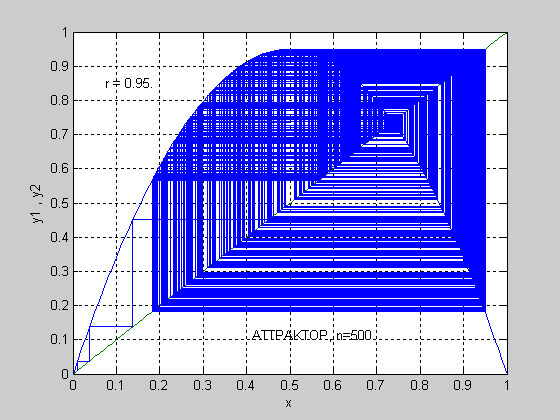
Рис. 7.5. Расширение области аттрактора: r=0.95, x₀=0.01, f_max=500

Несмотря на кажущееся случайное поведение модели в динамике, мы в действительности моделируем процессы, используя детерминированное логистическое уравнение. Следовательно, называть этот процесс стохастическим едва ли имеются основания. Мы имеем дело с детерминированным хаосом.

В результате моделирования мы получили наглядную картину того, что увеличение r, начиная со значения r>0.570, приводит к хаотическим режимам, которые в последующем имеют тенденцию усиления. Однако для хаоса характерно такое расположение всех траекторий процесса, при котором ни один из участков траектории не выходит за пределы определенной области на плоскости. Эта область является областью “притяжения” всех траекторий и называется аттрактором. Аттрактор расширяется с увеличением r, что свидетельствует об устойчивом хаотическом процессе и большом разнообразии хаотических структур, вызванных вариацией параметра r.