6. Моделирование динамических систем и электрических цепей средствами символьной математики

Моделирование в среде MatLAB, базирующееся на численных методах решения различных систем уравнений, позволяет в конечном счете получать результаты в цифровом виде, которые далее для эффективного восприятия интерпретируются системой графических построений и т.п. Как правило, такая информация скорее характеризует частное решение, чем общее. Вместе с тем, представление моделей и получение решений в аналитической форме является общим и может быть распространено на целый класс задач. Именно, исходя из общих правил выполнения математических операций, мы находим решения систем уравнений, производим операции интегрирования, дифференцирования различных функций, осуществляем поиск оптимальных решений и рациональных аналитических структур функций. И только на конечном этапе по полученному аналитическому решению выполняется количественная оценка, относящаяся к конкретной задаче в классе исследуемых проблем. Поэтому аналитическому решению, обладающему свойством общности, всегда отдается предпочтение.

В процессе выполнения громоздких математических преобразований, связанных с построением моделей и их упрощением, могут непроизвольно допускаться ошибки, неточности в записи промежуточных результатов. Тогда процедура моделирования и решения математических задач превращается в рутинную работу, требующую не только много энергии, но и связанную с непомерными затратами времени на получение корректных результатов. Вряд ли кто может утверждать, что при вводе в компьютер даже небольшой по объему информации он не допускал ошибок. Ведь не случайно на «отладку» программ требуется больше времени, чем на их разработку.

Система MatLAB с помощью пакета ‘Symbolic Math.’ позволяет пользователю автоматизировать получение аналитических решений [23]. Пакет содержит большой набор функций, предназначенных для решения в аналитическом виде систем уравнений, выполнения процедур интегрирования и дифференцирования, нахождения упрощенных математических выражений, получения аналитических решений с помощью прямого и обратного преобразований Лапласа и Фурье, а также позволяет решать многие другие задачи. Пакет может использоваться вместо специальных справочников с таблицами интегралов, функциями соответствия в частотной и временной областях и т.п. Для более подробного ознакомления с пакетом ‘Symbolic Math’ мы рекомендуем воспользоваться работой [20], в которой содержится также большое число интересных примеров.

6.1. Символьные выражения и алгебра

Для создания «символьных объектов» в среде MatLAB используется функция ‘sym’. Если использовать в основном окне MatLAB запись , то в результате будет создана символьная переменная с именем ‘’, а запись аналогично позволит создать символьную переменную ‘’. Записывая , мы можем придать переменной лишь действительные значения, а ввод выражения предполагает, что является недействительным. Приведенные выше записи позволяли создавать одну символьную переменную. Их, очевидно, удобно использовать в процессе коррекции решений, выполняемых в режиме прямых вычислений, т.е. без составления скрипт- файлов.

Гораздо чаще приходится вводить группы символьных параметров и переменных, для чего следует использовать функцию ‘syms’. Например, запись syms x y u v (переменные разделяются только пробелом) создает четыре символьных параметра x, y, u, v. Однако команда ‘syms’ не может использоваться для создания символьных констант. Для этих целей необходимо применять sym. Если требуется вести символьные вычисления, в процессе которых переменные могут принимать только действительные значения, необходимо воспользоваться следующей записью:

syms x y real.

В процессе использования ‘sym’ для создания символьных констант необходимо иметь ввиду, что записи , и создают символьные константы, не подлежащие вычислениям. В первом случае при нажатии клавиши ‘Enter’ будет выведено ‘pi’, во втором ‘1/3’ и в третьем ‘sqrt(2)’. Но если записать , то будут выполнены вычисления и получен ответ

.

Если же вновь возвратиться к символьной переменной sqroot2, то приводит к результату в символьной форме: .

Символьные константы можно воспринимать как числа, входящие в символьные выражения и служащие для корректной записи символьных формул.

Символьные переменные используются при записи различных функций и уравнений в качестве аргументов. Подобно тому, как мы обращаемся с переменными, производя вычисления, можно использовать при записи символьных математических выражений операторы сложения, вычитания, умножения, деления и возведения в степень. Например, запись в рабочем окне MatLAB

;

;

позволяет создать символьные переменные S и r. Иначе говоря, мы получим символьные выражения. Если до ввода этой информации аргументам x и y были присвоены численные значения, символьное выражение при обращении к r не возвратит результат в численном виде. Для возвращения численного значения функции требуется использовать специальные приемы, к рассмотрению которых мы возвратимся позже.

Все последующие преобразования могут быть выполнены в режиме прямых вычислений, а также проведены по блокам с помощью файла sah381.m, приведенного в конце параграфа. С этой целью мы будем использовать ссылки на соответствующие блоки программы.

Для записи матрицы в символьной форме, если ее элементами являются функции аргумента x, нет необходимости объявлять символьной всю матрицу. Достаточно использовать функцию syms лишь для самого . Предположим, что требуется создать матрицу из переменной . Тогда в символах может быть образована следующим способом (блок 1):

>> % Block 1.

n=4;

syms x

z=(0:n)'*(0:n);

A=x*z

A =

[ 0, 0, 0, 0, 0]

[ 0, x, 2*x, 3*x, 4*x]

[ 0, 2*x, 4*x, 6*x, 8*x]

[ 0, 3*x, 6*x, 9*x, 12*x]

[ 0, 4*x, 8*x, 12*x, 16*x]

>>

Очень часто в процессе преобразований необходимо восстановить информацию о том, какие переменные в выражении или матрице являются символьными. Для этого служит функция findsym (A). Если используется запись findsym (A, n), то будут возвращены только n аргументов, наиболее близких к . Поясним сказанное на примере формирования матрицы А1 из х, х1 и х2 в режиме прямых вычислений (блок 1):

>> n=4;

syms x x1 x2

v=(1:n)'*(1:n);

A1=x*v+x1./(v+ones(4,4))-x2*ones(4,4)

findsym(A1)

findsym(A1,2)

A1 =

[ x+1/2*x1-x2, 2*x+1/3*x1-x2, 3*x+1/4*x1-x2, 4*x+1/5*x1-x2]

[ 2*x+1/3*x1-x2, 4*x+1/5*x1-x2, 6*x+1/7*x1-x2, 8*x+1/9*x1-x2]

[ 3*x+1/4*x1-x2, 6*x+1/7*x1-x2, 9*x+1/10*x1-x2, 12*x+1/13*x1-x2]

[ 4*x+1/5*x1-x2, 8*x+1/9*x1-x2, 12*x+1/13*x1-x2, 16*x+1/17*x1-x2]

ans =

x, x1, x2

ans =

x,x1

>>

Элементы матрицы А1 являются функциями трех переменных. Запись findsym (A1) возвращает х, х1 и х2. Использование синтаксиса finsym (A1,2) возвращает лишь первые два аргумента: х и х1 как расположенную к х ближе, чем х2. В случае отсутствия символьных переменных, функция findsym возвращает «пустую» строку.

Теперь рассмотрим некоторые операции, связанные с преобразованиями функций.

Функция collect(f) позволяет привести все коэффициенты при переменных с одинаковыми показателями степени к одному сомножителю. Если функция содержит несколько переменных, например и , то запись collect (f, x2) позволяет выполнить операцию приведения только относительно . Рассмотрим пример (блок 1).

>> syms x1 x2

f1=(x1-2)^3+(x2-6)^2

collect(f1)

collect(f1,x2)

f1 =

(x1-2)^3+(x2-6)^2

ans =

x1^3-6*x1^2+12*x1-8+(x2-6)^2

ans =

x2^2-12*x2+(x1-2)^3+36

>>

Раскрытие функций выполняется с помощью expand(f). Например, если требуется возвести в квадрат сумму переменных и , то результат можно найти следующим образом (блок 2):

>> syms x y

z1=expand(tan(x+y))

z2=expand((x-y)^3)

z3=expand(1+cos(2*x))

z1 =

(tan(x)+tan(y))/(1-tan(x)*tan(y))

z2 =

x^3-3*x^2*y+3*x*y^2-y^3

z3 =

2*cos(x)^2

>>

Разложение функции на множители можно осуществить с помощью factor(f)

>> syms x y

>> z4=factor(x^3-3*x^2*y+3*x*y^2-y^3)

z4 =

(x-y)^3

>>

Одной из часто используемых возможностей функций в символьной форме является выполнение преобразований, упрощающих конечный результат в аналитическом виде. Символьные выражения допускают применение операторов суммирования, вычитания, умножения, деления и возведения в степень. Поэтому, наряду с рассмотрением в следующем примере возможности их использования, мы применим функцию simplify (f) для получения конечного результата. В режиме прямых вычислений определим сначала символьные переменные, а затем введем функции и . Затем разделим первую функцию на вторую и воспользуемся процедурой упрощения (блок 4):

>> % Block 4.

z4=x^3*y^2+6*x^3*y+9*x^3-12*x^2*y^2-72*x^2*y-108*x^2+48*x*y^2+...

288*x*y+432*x-64*y^2-384*y-576

z5=x^2*y^2-8*x*y^2+16*y^2+6*x^2*y-48*x*y+96*y+9*x^2-72*x+144

f=z4/z5

v=simplify(f)

z4 =

x^3*y^2+6*x^3*y+9*x^3-12*x^2*y^2-72*x^2*y-108*x^2+48*x*y^2+288*x*y+432*x-64*y^2-384*y-576

z5 =

x^2*y^2-8*x*y^2+16*y^2+6*x^2*y-48*x*y+96*y+9*x^2-72*x+144

f =

(x^3*y^2+6*x^3*y+9*x^3-12*x^2*y^2-72*x^2*y-108*x^2+48*x*y^2+288*x*y+432*x-64*y^2-384*y-576)/(x^2*y^2-8*x*y^2+16*y^2+6*x^2*y-48*x*y+96*y+9*x^2-72*x+144)

v =

x-4

>>

Видно, что f по завершении преобразований представляется в исключительно простом виде:

.

Если выражение состоит из слагаемых, записанных в форме дроби, то применение функции позволяет получить ответ в виде отношения двух полиномов – числителя и знаменателя. Проиллюстрируем приведение к общему знаменателю на простом примере (блок 5).

>> % Block 5.

f1=x^2+3

f2=2/(x-4)

f=f1+f2

[num,den]=numden(f)

f1 =

x^2+3

f2 =

2/(x-4)

f =

x^2+3+2/(x-4)

num =

x^3-4*x^2+3*x-10

den =

x-4

>>

К символьным константам применима функция double(v), которая преобразует выражение v в числовую форму (блок 6). Если, например, записана константа , то

позволит получить ответ в символьной форме:

.

В случае же использования double будут выполнены вычисления

Две функции ‘sym2poly’ и ‘poly2sym’ позволяют преобразовывать функции в символьной записи к символьному полиному и обратно.

Рассмотрим пример (блок 7).

>> % Block 7.

syms x

f=3*x^2+4*x+1

v1=sym2poly(f)

v2=poly2sym(v1)

v3=poly2sym(v1,'y')

f =

3*x^2+4*x+1

v1 =

3 4 1

v2 =

3*x^2+4*x+1

v3 =

3*y^2+4*y+1

>>

В последнем случае создана функция переменной по заданному полиному.

Если требуется произвести замену аргументов в символьном выражении, можно воспользоваться функцией подстановки , -символьное выражение, -старый аргумент, -новый аргумент. Конечно, новый аргумент также должен предварительно объявляться символом (блок 8).

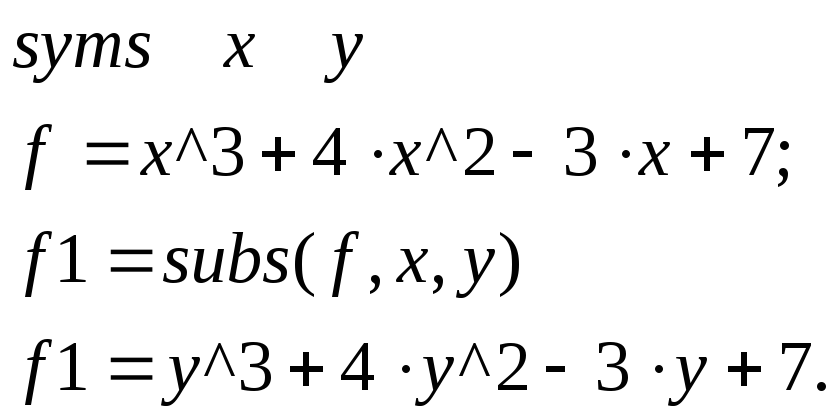
Для записи математических выражений в форме, близкой к принятой в учебных курсах математики, можно воспользоваться оператором pretty. Например, запись

pretty(f1)

возвращает результат (блок 8):

Однако в таком виде математическое выражение не может быть использовано в дальнейших символьных преобразованиях. Оно как бы играет вспомогательную роль и позволяет упростить процесс составления решений, полученных вручную и в символьной записи [49].

Если необходимо задать функцию какой-либо переменной, например, функцию времени , то следует воспользоваться оператором . По завершении ввода к этой функции можно применять операции, предусмотренные символьной оболочкой. Для создания, например, функции необходимо выполнить ввод информации в такой последовательности (блок 9):

>> % Block 9.

syms t

v=sym('v(t+2)')

g=subs(v,t+2,t+1)

r=subs(g,t+1,t)

f=v+3*g-2*r

v =

v(t+2)

g =

v(t+1)

r =

v(t)

f =

v(t+2)+3*v(t+1)-2*v(t)

>>

Рассмотрим, как с помощью функции подстановки можно записать факториал и вычислить его значение при (см. блок 10).

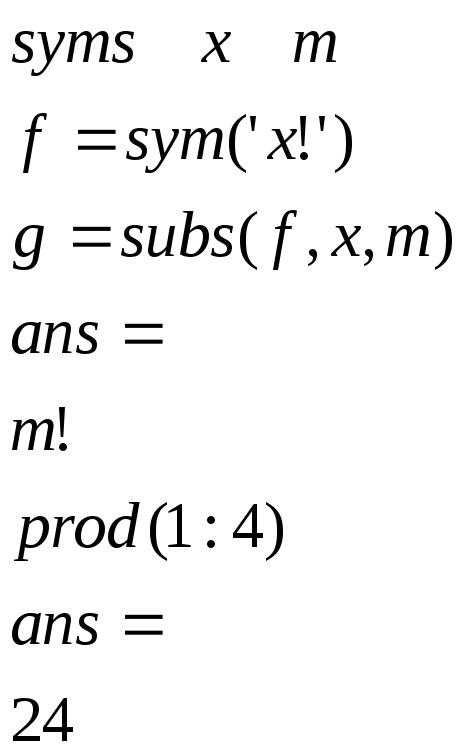
Функция подстановки ‘subs’ может использоваться для замены сразу нескольких аргументов. При этом в фигурных скобках необходимо перечислить «старые» аргументы, а затем – в требуемой последовательности замены – привести «новые элементы», как показано ниже (блок 11):

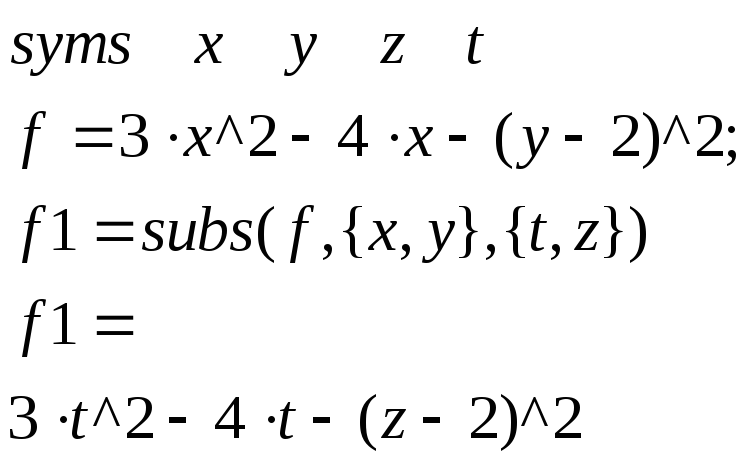
Когда возникает потребность в численной оценке функции или графических построениях, с помощью оператора подстановки следует сначала аргументы заменить константами (числами), а затем использовать нам уже знакомую функцию ‘double’ для получения окончательного результата:

Заметим, что представлена в символьной форме, является результатом вычислений. Если расчетное значение является малым, с помощью оператора vpa можно задать требуемое количество разрядов (не большее 32). Синтаксис функции очень прост:

где - число разрядов.

Графические построения функций одной переменной, представленных в символьной форме, выполняются с помощью функции . По умолчанию аргумент изменяется в диапазоне [-2pi 2pi]. В других случаях возможно задать нижнюю и верхнюю границы с помощью вектора [x_min , x_max]. Приведем пример построения графика гармонического сигнала (блок 12, рис. 6.1):

и экспоненты

По осям абсцисс и ординат, используя xlabel и ylabel, мы можем нанести требуемый текст и в графическом окне выполнить обработку изображенных зависимостей. Обычным способом может быть нанесена сетка:

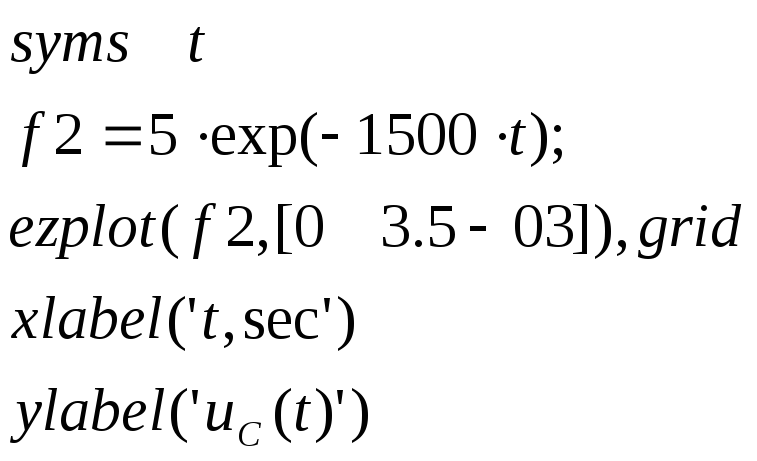
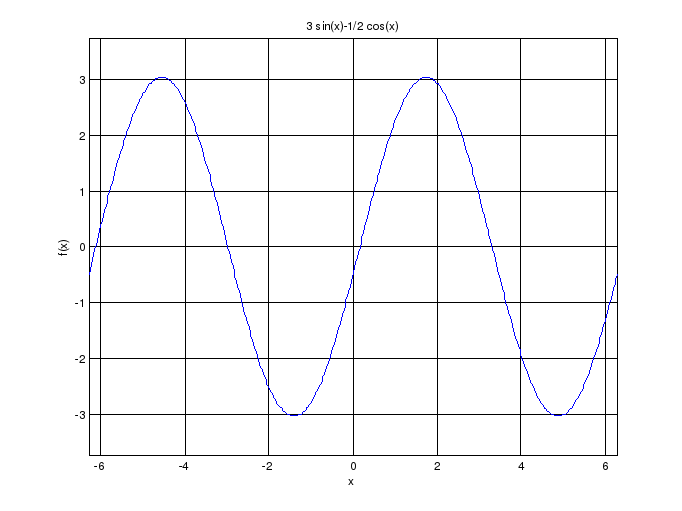
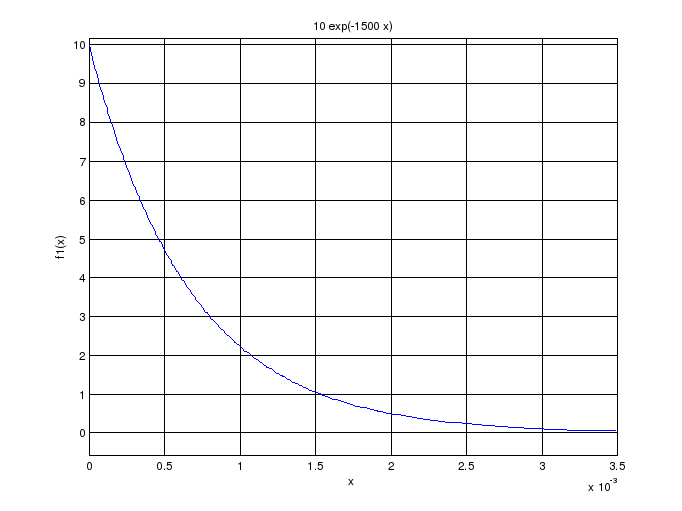
Рис. 6.1. Графики функций f и f1.

Все перечисленные выше операции над символьными выражениями выполняются с помощью файла sah381.m.

% File 'sah381.m'

% File to paragraph 6.1

%=========================

% Block 1.

n=4;

syms x

z=(0:n)'*(0:n);

A=x*z

%--------------------------

n=4;

syms x x1 x2

v=(1:n)'*(1:n);

A1=x*v+x1./(v+ones(4,4))-x2*ones(4,4)

findsym(A1)

findsym(A1,2)

%---------------------------

syms x1 x2

f1=(x1-2)^3+(x2-6)^2

collect(f1)

collect(f1,x2)

%============================

% Block 2.

syms x y

z1=expand(tan(x+y))

z2=expand((x-y)^3)

z3=expand(1+cos(2*x))

%==========================

% Block 3.

f1=(x-4)^3*(y+3)^2

f2=(y+3)^2*(x-4)^2

z4=expand(f1)

z5=expand(f2)

f=z4/z5

v=simplify(f)

%=============================

% Block 4.

z4=x^3*y^2+6*x^3*y+9*x^3-12*x^2*y^2-72*x^2*y-108*x^2+48*x*y^2+...

288*x*y+432*x-64*y^2-384*y-576

z5=x^2*y^2-8*x*y^2+16*y^2+6*x^2*y-48*x*y+96*y+9*x^2-72*x+144

f=z4/z5

v=simplify(f)

%==========================

% Block 5.

f1=x^2+3

f2=2/(x-4)

f=f1+f2

[num,den]=numden(f)

%==========================

% Block 6.

v=sym('sin(pi/4)')

s=4*v

z=double(s)

%==========================

% Block 7.

f=3*x^2+4*x+1

v1=sym2poly(f)

v2=poly2sym(v1)

v3=poly2sym(v1,'y')

%==========================

% Block 8.

f=x^3+4*x^2-3*x+7

f1=subs(f,x,y)

pretty(f1)

%===========================

% Block 9.

syms t

v=sym('v(t+2)')

g=subs(v,t+2,t+1)

r=subs(g,t+1,t)

f=v+3*g-2*r

%============================

% Block 10.

syms m

f=sym('x!')

g=subs(f,x,m)

prod(1:4)

%=============================

% Block 11.

syms x y z t

f=3*x^2-4*x-(y-2)^2

f1=subs(f,{x,y},{t,z})

f2=subs(f1,{t,z},{1,3});

f3=double(f2)

class(f1)

class(f3)

vpa(f3,4)

%===============================

% Block 12.

f=3*sin(x)-0.5*cos(x)

ezplot(f),grid

ylabel('f(x)')

pause

syms x y

f1=10*exp(-1500*x)

ezplot(f1,[0,3.5e-03]),grid

ylabel('f1(x)')

pause

f2=5*exp(-1500*t)

ezplot(f2,[0 3.5e-03]),grid

xlabel(' t,sec')

ylabel(' Uc(t) ')

Как было отмечено выше, операции разделены на блоки. В процессе работы файла предусмотрен вывод графиков. После просмотра очередного графика, фиксируемого на дисплее с помощью оператора ‘pause’, дальнейшие вычисления продолжаются нажатием клавиши ‘Enter’.