2. Динамические системы с тремя накопителями энергии

В качестве динамической системы, содержащей три элемента, способных накапливать энергию, рассмотрим электрическую цепь, изображенную на рис. 5.15.

Цепь содержит два тиристора, на управляющие электроды 1 и 2 которых поочередно подаются сигналы управления.

Можно отметить два состояния. В первом состоянии открыт, а закрыт. Пренебрегая сопротивлениями переходов «анод-катод» тиристоров в открытом состоянии, для построения динамической модели мы можем использовать цепь, представленную на рис. 5.16а. Во втором состоянии закрыт. Структура цепи изменилась. Поэтому для составления модели во втором состоянии необходимо воспользоваться цепью, изображенной на рис. 5.16б.

Будем считать, что основными переменными состояния цепи являются , и (см. обозначения на рис. 5.15).

Вектор переменных состояния , вектор начальных условий: .

Уравнения для цепи в первом состоянии (рис. 5.16 а):

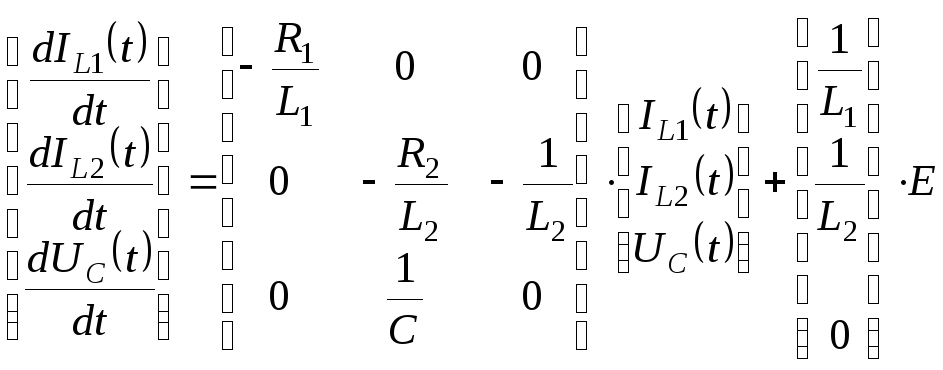
(5.0)

Уравнения для цепи во втором состоянии (рис. 5.16 б):

(5.0)

Поскольку переход цепи из состояния в состояние происходит практически мгновенно (время переключения тиристоров существенно меньше периода следования управляющих импульсов), а основные переменные состояния не изменяются скачком, решения уравнений (5.73) и (5.74) необходимо «сшивать» на границах по правилу: правая граница предшествующего режима является левой границей последующего режима.

В общем виде уравнения (5.73) и (5.74) могут быть решены в терминах собственных значений матрицы динамических систем с тремя накопителями энергии, которые в MatLAB определяются с помощью функции .

Рассмотрим два режима, встречающихся наиболее часто на практике.

Первый режим. Соответствует трем различным действительным собственным значениям

(5.0)

матрицы .

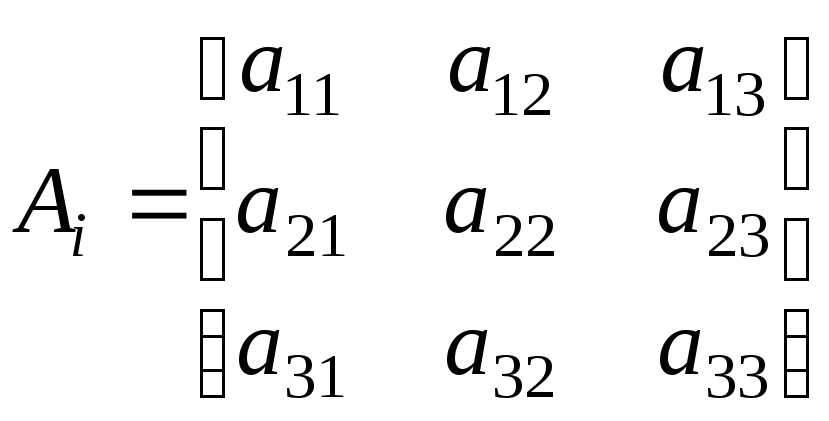Матричный экспонециал:

(5.0)

Обозначим . Вектор функций может быть вычислен с помощью матрицы Вандермонда:

(5.0)

Полученные аналитические зависимости из (5.77) имеют вид:

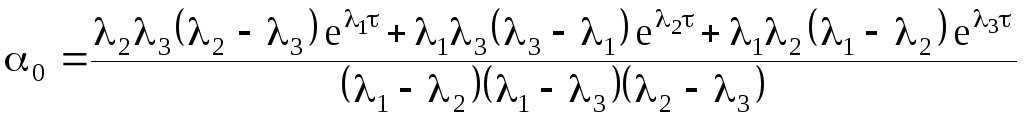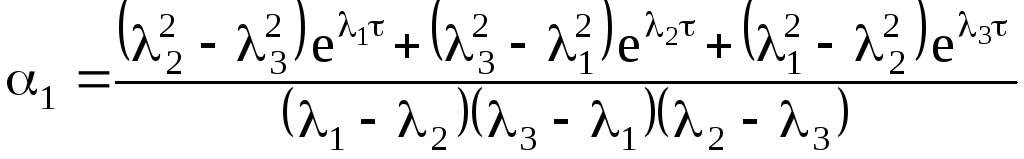(5.0) 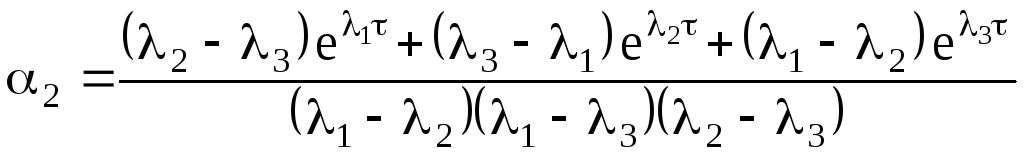(5.0) (5.0)

Вычислив , и по приведенным формулам, мы должны сначала определить с помощью (5.76), а затем решить уравнение:

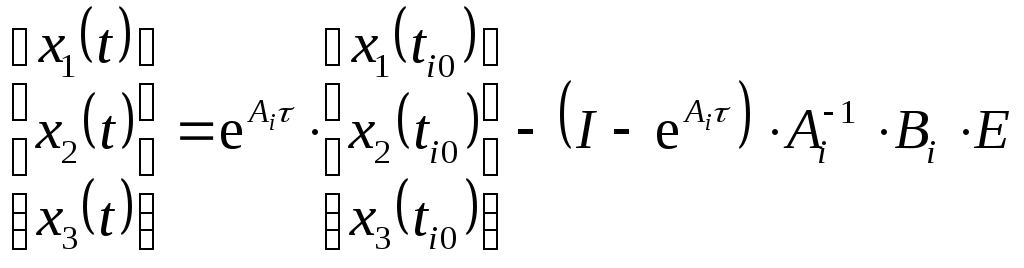(5.0)

Инверсную матрицу можно представить в терминах элементов : 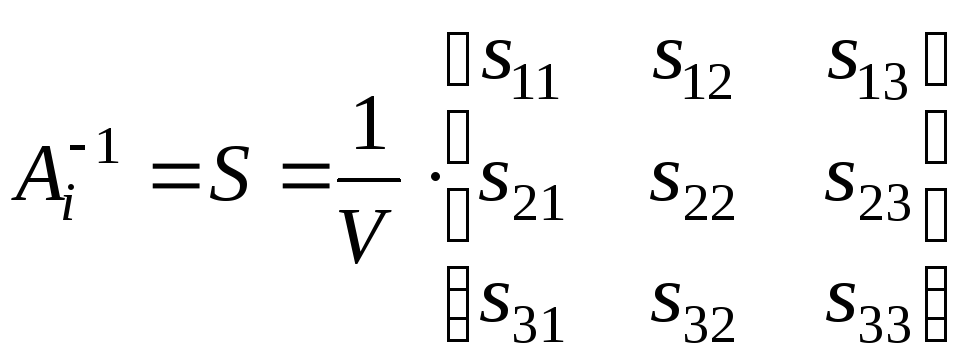, где ,

Второй режим. соответствует одному действительному собственному значению и двум комплексно-сопряженным корням: и . В этом случае расчет переходного процесса выполняется также по формуле (5.81), однако , и , входящие в выражение матричного экспоненциала, необходимо рассчитывать по формулам:

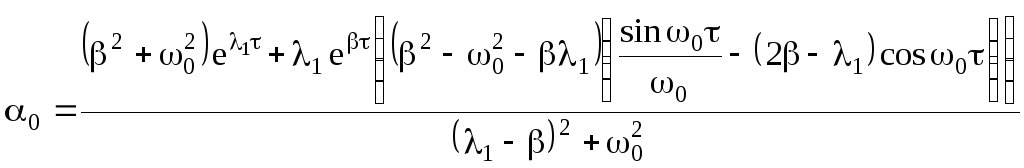(5.0) (5.0) (5.0)

Аналитические зависимости для случая кратных корней не приводятся, так как эти режимы на практике не являются определяющими. Однако они могут быть получены как частный случай решения задачи, соответствующей первому режиму.