Введем векторы

s = [s₁ s₂ ... s_m]^T, х = [a, а₂ ... a_n]^T, v = [v₁ v₂ … v_m]^T.

Из входных данных образуем прямоугольную матрицу H размерно­сти

(т x n)

Тогда (1.10) можно записать в векторно-матричной форме:

(1.11)

Если т > n, то система (1.11), представляющая собой модель изме­рителя, является переопределенной. Тогда можно найти такие значения элементов вектора x =, при которых разность

(1.12)

точнее — скалярное произведение будет принимать минималь­ное значение. Задачу минимизации скалярного произведения сформулиру­ем следующим образом: определим вектор , при котором минимизи­руется критерий качества

(1.13)

Постоянное число 1/2, содержащееся в(1.13) на вектор x* не влия­ет. Оно введено для удобства вычислений.

Если H в критерии качества (1.13) имеет минимальный ранг, равный n, то минимум J(х) можно найти путем дифференцирования J пo x и при­равнивания производной к нулю. Это необходимое условие оптимально­сти. Достаточным условием минимума функции одной переменной следу­ет считать положительное значение второй производной в экстремальной точке, а для функции нескольких переменных должно выполняться усло­вие Лежандра-Клебша.

Рассмотрим произведение двух вектор-функций:

где 'Т" – знак транспонирования.

Согласно правилам векторного дифференцирования, можно записать

Используя это выражение, приравняем и Тогда необходимое условие оптимальности можно пред­ставить следующим образом:

(1.14)

или

Информационная матрица имеет размерность (n x n) и явля­ется неособенной, поскольку H имеет максимальный ранг. Тогда, умножая левую и правую части (1.14) слева на инверсную матрицу , по­лучим наилучшую оценку вектора x

(1.15)

Получив наилучшую оценку вектора , подставим это значение в уравнение (1.11) и определим вектор у_м как результат моделирования

(1.16)

Качество моделирования можно оценить по вектору разности между исходными данными s и моделью s_м

z = s – s_м

Уравнение (1.15) гарантирует получение минимума суммы квадра­тов элементов вектора z, т.е.

(1.17)

Для оценки эффективности моделирования можно воспользоваться эвклидовой нормой. B среде MatLAB существует функция "norm(z,'fro')", предназначенная для ее определения. Напомним, что эвклидова норма вектора z представляет собой равенство evc = = . Следовательно, критерий качества (1.17) можно записать

Другой подход к получению (1.15) может состоять в следующем. Рассмотрим вновь переопределенную систему, представленную уравнением (1.11). Предположим, что v имеет нормальное распределение, а вектор s состоит из постоянных значений. Тогда Hdx = dv и, следова­тельно, dv^T = dx^T = Н^T.

Для переопределенной системы уравнений справедливо условие т > n . Умножим dv^T справа на вектор v и подставим его значение из уравнения (1.11)

(1.18)

Если теперь ввести критерий оценки вектора x, при котором требу­ется минимизировать

при отсутствии ограничений, то можно получить

(1.19)

Запишем (1.19) в векторно-матричной форме

(1.20)

Поскольку (1.20) совпадает с (1.18), то равенство указанного ска­лярного произведения векторов нулю возможно только в том случае, если . Данное условие может быть выполнено, если оценка х, которую ранее мы обозначили как ,будет

Мы получили уравнение, точно совпадающее с (1.16). Сумма квад­ратов погрешностей — скалярное произведение

Теперь умножим левую и правую части (1.11) слева на матрицу размерности (nЧm). Заметим, что и поэтому

где - вектор погрешности, представляющий разность между оценочным

истинным значениями вектора параметров.

Предполагая, что H и v независимы, мы получим среднее значение, равное нулю

(1.21)

Уравнение (1.21) подтверждает несмещенность оценки.

Уравнение (1.15) может быть использовано для оценки коэффици­ентов нелинейных функций, которые путем замены переменных приводят­ся к выражениям, линейным относительно неизвестных параметров. Све­дем некоторые из них в таблицу 1.1, которая может быть полезна при выполнении практических преобразований.

Заметим, что использование функций, расположенных во втором столбце таблицы, для оценки параметров исходных зависимостей позволя­ет

Таблица 1.1.

№	Исходная нелинейная функция	К какому виду приводится	Замена переменных
1.	y =Aekx	Z = a0 + a1x	Z = ln y
2.	y =Bxb	Z = a0 + a1u	Z = ln y, u = ln x, a0 = lnB, a1 = b
3.		Z = a0 + a1u	u =1/x
4.		Z = a0 + a1u	u =1/xb
5.		Z = a0 + a1x + а2х2	Z = ln y, , ,

получить минимум суммы квадратов для преобразованных функций. Для исходных уравнений, являющихся нелинейными, применение нели­нейных методов оценивания позволяет получить меньшее (в сравнении с MНK) значение эвклидовой нормы. Оценка же параметров функции Z по­зволяет лишь приблизиться к наилучшей оценке y.
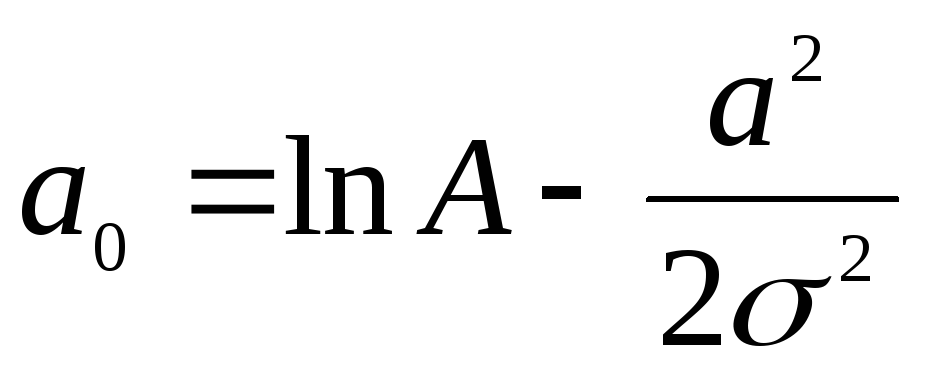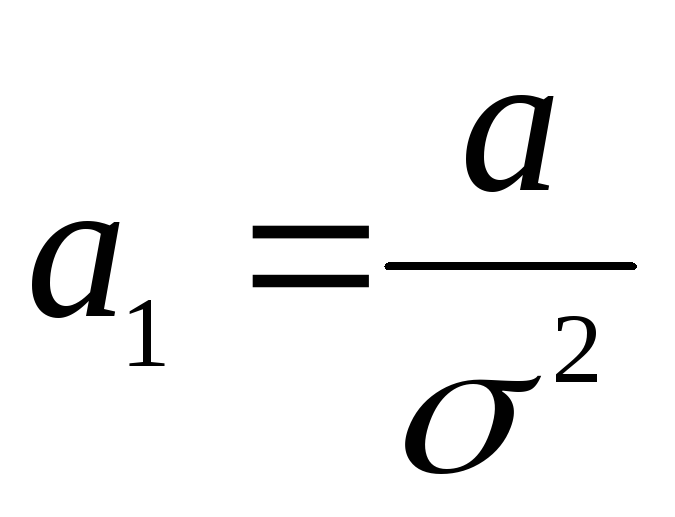