1.7. Оценивание параметров по критерию минимума среднего абсолютного значения остатков

Выбрав р = 1, мы имеем оценку среднего абсолютного значения ос­татков. B отличие от метода наименьших квадратов, где для минимума критерия качества получено математическое выражение путем взятия про­изводной и приравнивания ее нулю, минимизация средней абсолютной оценки таким способом невозможна, так как J₁(x) не может быть диффе­ренцирована для всех значений x. Поэтому для поиска минимума J₁(x) мoгyт быть использованы определенные формы решения задач ли­нейного программирования, базирующиеся на интерполяционном процес­се по группе точек, в которых произведены измерения.

Обобщенная линейная задача аппроксимации по критерию минимума среднего абсолютного значения остатков может быть сформулирована следующим образом. По заданным измерениям y_i, i = 1,..., m, требуется оценить n-мерный вектор x, при котором выполняются условия

(1.53)

и x доставляет минимум критерию качества

(1.54)

Запишем H размерности (m x n ), состоящую из т строк, отвечающих уравнениям (1.53)

где ..…………………………

Известно, что если столбцовый ранг матрицы H равен k  n , то наилуч­шая оценка J₁ (x) определяется на множестве из k измерений, выбранных из у₁, y₂,…, y_m . Следовательно, если имеются т измерений и n известных векто­ров H_j, j= 1,..., n, то при ранге матрицы Н, равном k,функция

являющаяся наилучшей оценкой по критерию , точно интерполирует, по крайней мере, k измерений. Напомним, что оценка по критерию не обязательно должна удовлетворять этому условию. Гиперпло­скость вообще может не проходить через какую-либо экспериментальную точку, в то время как минимум суммы наименьших квадратов будет обеспечен.

Решение линейной задачи по минимизации (1.54) может быть полу­чено с помощью одного из известных алгоритмов, описанных в литерату­ре. Однако, можно предложить очень эффективный вычислительный алго­ритм, базирующийся по структуре на двухступенчатом решении. C этой целью запишем (1.54) в следующем виде:

(1.55)

Очевидно, мы вправе полагать, что минимуму (1.55) соответствуют значения

(1.56)

………..

Применяя это же условие к критерию (1.54), будем иметь

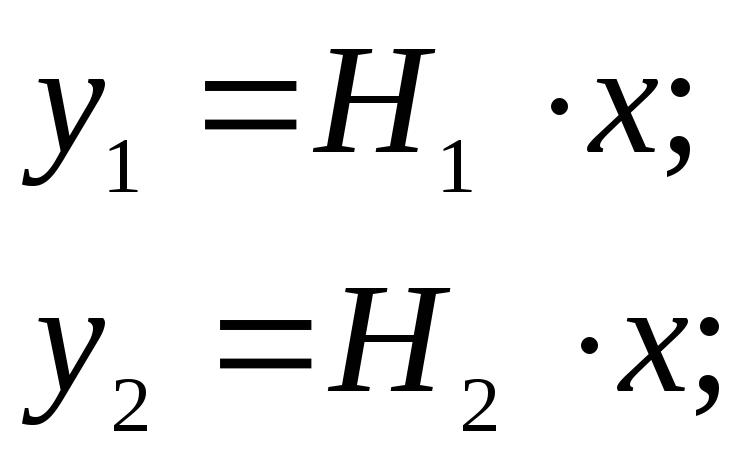(1.57)

……………..

Система (1.56) содержит т уравнений с n неизвестными. Для пере­определенной системы мы не можем обеспечить условие (1.56). Поэтому на первой ступени решения (1.57) ограничимся приближением, соответст­вующим минимуму критерия J₂ , т.е. получим оценку методом наимень­ших квадратов (см. формулу 1.15)

Определим остатки для каждого измерения и получим систему уравнений

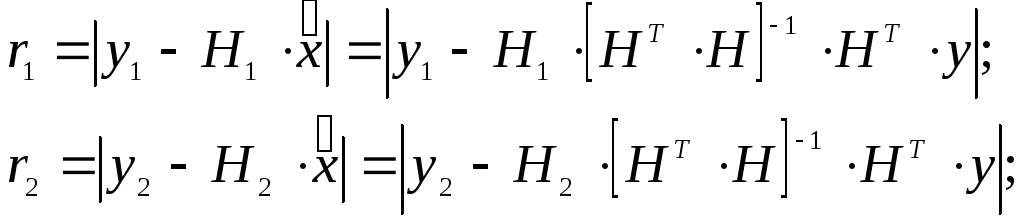(1.58)

……. ……. ……. ……. ……. ……. ……. …..

.

Если ранг H равен k, причем k  n, то для наилучшей оценки x по критерию J₁ оцениватель должен обеспечить точное прохождение гиперп­лоскости через k точек из всех измерений, входящих в вектор у. При этом выбранные точки должны иметь наименьшие остатки.

Ha второй ступени решения, сформировав вектор из уравнений (1.58), мы можем выполнить сортировку r в порядке возрастания его элементов. C этой целью в среде MatLAB восполь­зуемся оператором и получим матрицу, содержащую строку rl и строку I, содержащую индексы, использованные при сортировке.

Для определенности положим, что k = n, т.е. матрица H имеет пол­ный ранг. Тогда вектор rl можно представить в виде блоков :

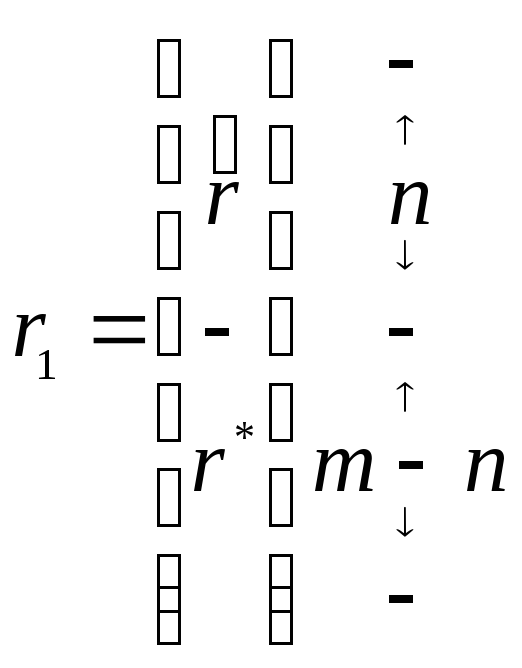(1.59)

где - (n Ч 1)- вектор, содержащий наименьшие остатки,

- вектор, в который вошли все оставшиеся r_i , определен­ные системой (1.58).

Аналогично разделим матрицу H на два блока размерности (nЧn) и - матрицу

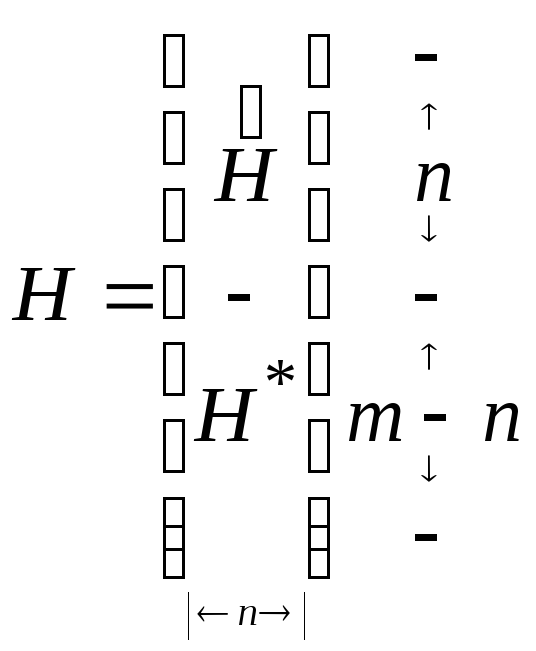(1.60)

Уравнения, входящие в первый блок, можно представить как

(1.61)

где - вектор; - квадратная матрица х - (nЧ1) - вектор. Решение (1.7-9) определим путем инверсии :

(1.62)

Мы получим наилучшую оценку по критерию J₁. Далее нетрудно определить вектор остатков

(1.63)

Для иллюстрации "работы" алгоритма, представленного системой уравнений (1.551.63), возвратимся вновь к примеру построения моде­ли наблюдателя, параметры которого оцениваются по экспериментальным данным в точках (1, 2), (2, 2), (3, 3), (4, 4), (5, 3):

Необходимо оценить коэффициенты а₁ и а₂ по критерию минимума эвклидовой нормы при условии, что должно точно выполняться ограничение , где С = [1,б], d= = [5].

Согласно (1.60) матрица Н будет иметь вид

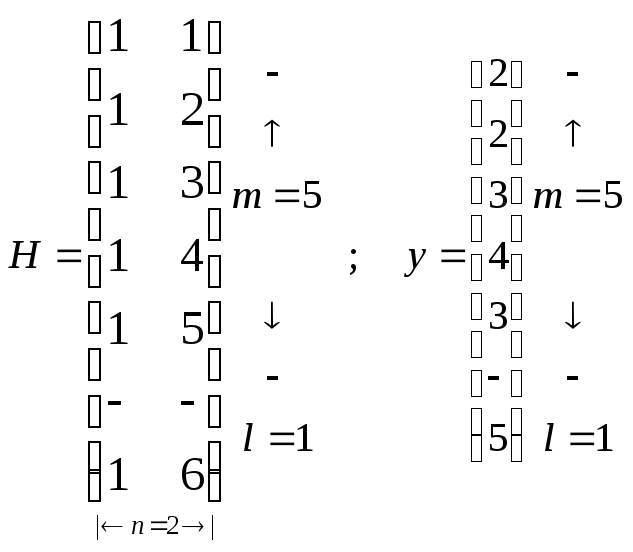
Для оценки методом наименьших квадратов воспользуемся формулой

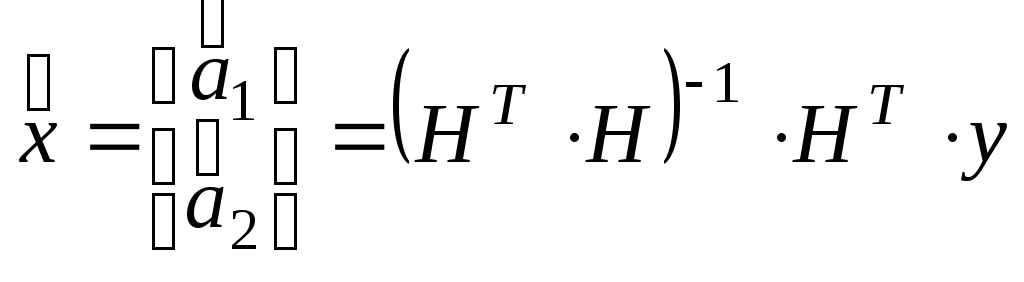
B результате для матрицы H размерности (5Ч2) будем иметь

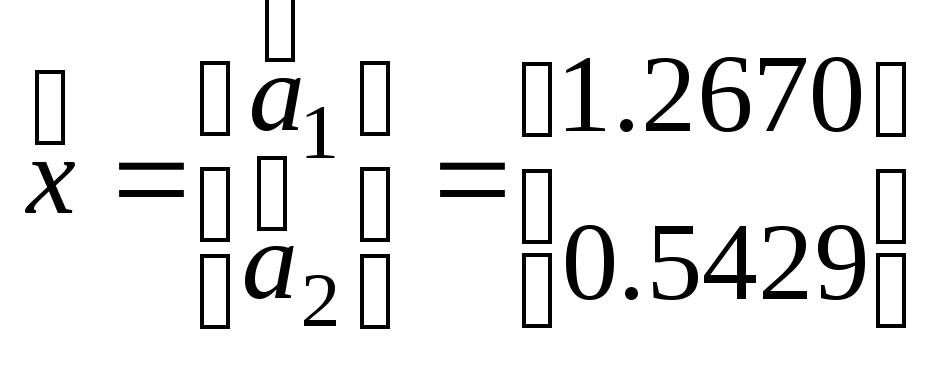
и, следовательно, в соответствии с (1.58), вектор остатков

Так как ранг матрицы H равен 2, процедура оценивания должна со­стоять в "пригонке" лишь двух точек, через которые должна проходить прямая . Эти точки должны соответствовать первому и треть­ему элементам вектора r. Однако по условиям ограничений эта же прямая должна проходить через точку с координатами (6, 5). Следовательно, вме­сто точки (1, 2), для которой справедливо , необходимо ввести координаты (6, 5). Тогда, согласно (1.60), матрица

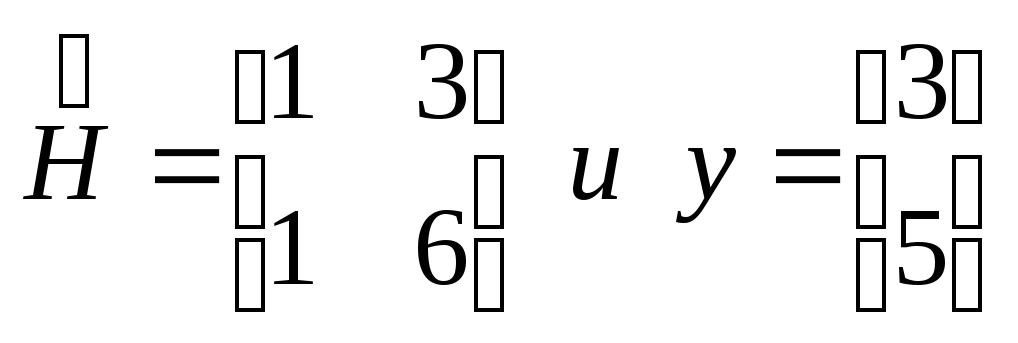
Оптимальная оценка по критерию J₁