6.2. Алгебраические и трансцендентные уравнения. Расчет цепи постоянного тока

Инструментарий символьной математики может эффективно использоваться для решения систем алгебраических и трансцендентных уравнений. Напомним, что трансцендентные уравнения содержат одну или несколько функций вида или . Решателем уравнений является solve. Запись solve(f) позволяет получить решение f в символьной форме. Для системы функциональных уравнений f₁, f₂,…, f_n, содержащих символьные аргументы, необходимо использовать синтаксис:

solve(f₁, f₂,…, f_n).

Остановимся кратко на трех способах записи и решения уравнений с помощью функции solve.

Первый способ предполагает использование формы:

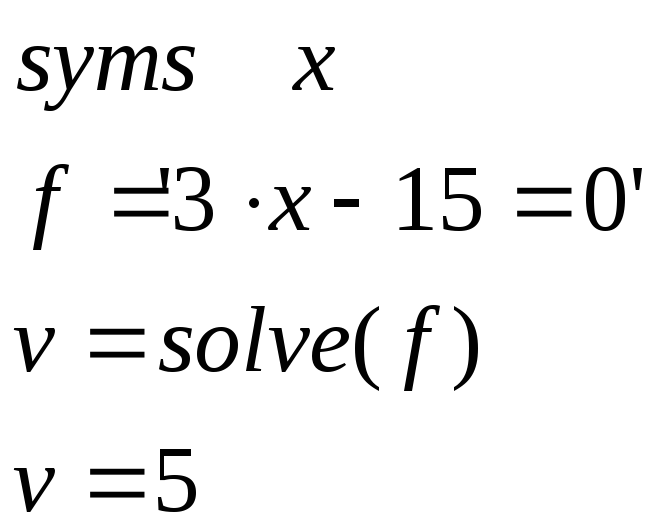
Второй способ допускает запись уравнения непосредственно в круглых скобках:

Третий способ позволяет определить нули уравнения. Он не требует выделения функции в апострофах, как в предыдущем случае

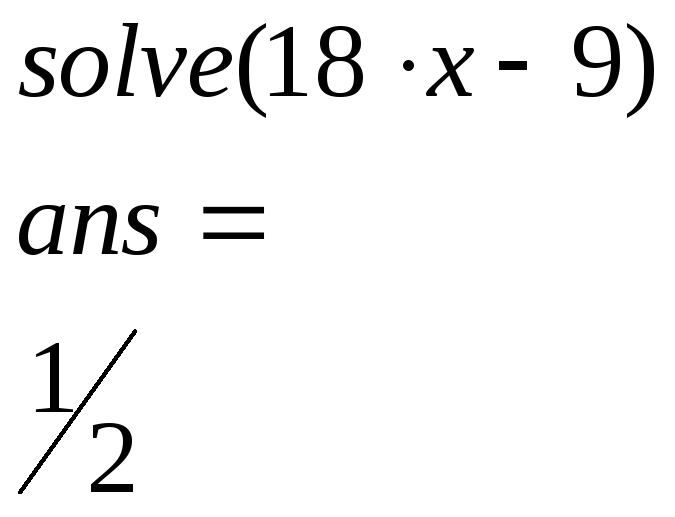
Кроме алгебраических уравнений, с помощью функции solve возможно решать трансцендентные уравнения. Предположим, что переходный процесс в электрической цепи описывается уравнениями (см. [4], с.348, формула 13):

(6.1)

Требуется найти время , при котором и . Мы предварительно нашли эти значения, подставив в формулы (6.1) время с. Теперь с помощью solve попытаемся решить обратную задачу. С этой целью объявим символьной переменной и запишем систему уравнений в привычной для нас форме:

syms t real

Uc=150+79.61*exp(-61*t)-29.61*exp(-164*t)

i2=1.5+1.146*exp(-61*t)-1.646*exp(-164*t)

t1=solve(150+79.61*exp(-61*t)-29.61*exp(-164*t)-177.2740);

t2=solve(1.5+1.146*exp(-61*t)-1.646*exp(-164*t)-1.8097)

Сразу отметим, что решение этой задачи не является тривиальным. В процессе определения будет получено несколько десятков решений в логарифмической форме, содержащих мнимые составляющие. Они, безусловно, должны быть отброшены. Однако среди всех решений два заслуживают внимания. Скопируем их с дисплея.

Аналогично поступим, анализируя решение для .

Эти четыре решения и приведены ниже:

-log(.98374022559907422805633257503713)

ans =

0.0164

-log(1.0072014641657529993853150505161)

ans =

-0.0072

-log(.98374115476077051948459419838182)

ans =

0.0164

-log(.98956541557254351733207873595075)

ans =

0.0105

Первые два решения – оценки , из которых видно, что время не может быть отрицательным, и должно быть принято

, т.е. 1/61 c.

Третье и четвертое решения получены для . Обратим внимание на то, что мы имеем два положительных числа:

Следовательно, ток принимает значение, равное 1.8097 А, в двух точках. Действительно, подставляя в формулу (4.2-1), мы получим . Однако, по условию задачи требовалось определить время, когда вышеприведенные значения и наблюдаются в один и тот же момент времени. Поэтому

.

Далее остановимся на решении уравнений, содержащих более одной переменной. Одно уравнение с двумя аргументами с помощью функции solve решается относительно той переменной, которая указана после записи уравнения. Если же аргумент не указан, решение по умолчанию выполняется относительно переменной, расположенной в порядке алфавита ближе к . Рассмотрим пример. Предположим, что требуется получить решение уравнения

.

Не объявляя символьных переменных, мы воспользуемся простой записью:

>> solve('a^2+2*a+4-b=0')

ans =

a^2+2*a+4

>> solve('a^2+2*a+4-b=0','b')

ans =

a^2+2*a+4

>> solve('a^2+2*a+4-b=0','a')

ans =

[ -1+(-3+b)^(1/2)]

[ -1-(-3+b)^(1/2)]

>>

Как следует из приведенного решения, сначала получено значение ‘b’ в терминах ‘a’ (‘b’ по последовательности в алфавите ближе к ). Затем, указав ‘b’ после функции, мы получили тот же результат. Когда же использовали ссылку на аргумент ‘a’, то для него в терминах ‘b’ были выведены два решения, соответствующие корням квадратного уравнения: .

Перейдем к решению системы алгебраических уравнений, записанных в символьной форме.

Рассмотрим электрическую цепь постоянного тока, представленную на рис. 6.2( см. также раздел 2.1, рис.2.1):

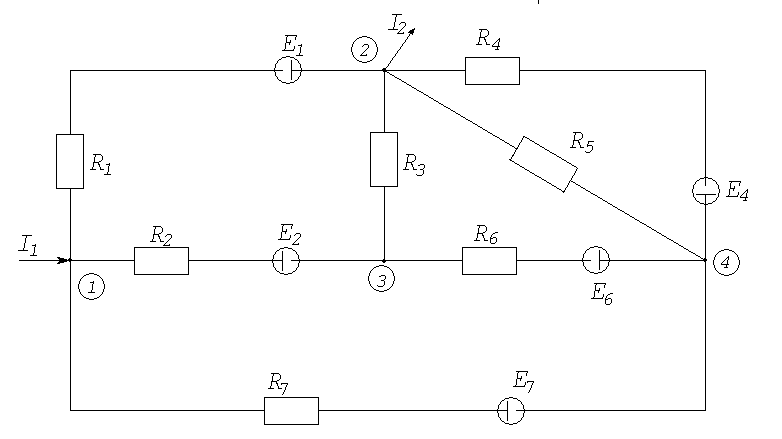
Рис. 6.2. Расчет цепи постоянного тока с помощью пакета