
- •В.И. Королев, в.В. Сахаров, о.В. Шергина оценка параметров, моделирование динамических систем и электрических цепей в среде matlab
- •Санкт-Петербург
- •Рецензенты:
- •Isbn 5-88964-073-X © Королев в. И.,
- •Содержание
- •1. Идентификация параметров моделей систем на основе квадратичных методов оценивания………..……………………………………………………………........................... 11
- •Модели установившихся режимов в электрических цепях и
- •4. Модели пространства состояний в электрических цепях и
- •5. Системы и цепи под воздействием параметрических возмущений: численные и
- •6. Моделирование динамических систем и электрических цепей средствами
- •8. Моделирование технологических процессов в системах с помощью
- •Введение
- •Идентификация параметров моделей систем на основе квадратичных методов оценивания
- •Линейные модели систем Рассмотрим систему линейных уравнений
- •Рассмотрим линейное уравнение
- •Для существования точного решения уравнения (1.1) должно выполняться условие
- •1.2. Переопределенные системы уравнений. Метод наименьших квадратов
- •Введем векторы
- •1.3. Оценивание параметров периодических сигналов по экспериментальным данным
- •Таким образом, требуется оценить амплитуды и фазы
- •Разделив период t на 24 равных интервала, мы получим . Так как , то каждому будет соответствовать угол (в градусах).
- •1.4. Рекуррентный метод оценивания параметров моделей
- •1.5.Алгоритм оценивания параметров моделей в условиях ограничений
- •Минимальное значение (1.43) соответствует условию
- •1.6. Нормы оценивания параметров в теории инверсных систем
- •1.7. Оценивание параметров по критерию минимума среднего абсолютного значения остатков
- •Уравнение измерителя
- •1.8. Нелинейное оценивание параметров моделей в режиме прямых вычислений
- •1.9. Алгоритм ортогонализации в оценке параметров динамических систем
- •Рассмотрим нелинейную дискретную модель системы
- •2. Модели установившихся режимов в электрических цепях и системах
- •2.1. Пример модели цепи постоянного тока
- •Пример модели цепи переменного тока
- •2.3.Несимметричные режимы в трехфазных электрических цепях: метод симметричных составляющих
- •2.4. Модель многоузлового разветвления русла в стационарном режиме. Аналогии с электрической цепью
- •2.5. Модель твердого тела с двумя неподвижными точками
- •2.6. Многопродуктовая модель экономики: межотраслевой баланс
- •2.7. Модель оценки элементов матрицы преобразования
- •3. Динамические звенья и системы под воздействием гармонических сигналов
- •3.1.Построение частотных характеристик простых динамических звеньев
- •3.2.Резонанс в динамических системах
- •3.4. Резонанс в электрических цепях
- •3.4. Режим биений
- •4. Модели пространства состояний в электрических цепях и системах
- •4.1. Понятие состояния
- •4.2. Уравнения состояния для электрических цепей
- •4.3. Приведение к резистивной форме моделей электрических цепей с одним накопителем энергии
- •4.4. Определение коэффициентов дифференциальных уравнений моделей электрических цепей с двумя накопителями энергии
- •4.5. Электрическая цепь с четырьмя накопителями энергии
- •4.6. Примеры составления уравнений состояния rlc -цепей в матричной форме
- •Исходная цепь
- •Краткие сведения о решателях дифференциальных уравнений
- •5.2. Об аналитическом решении дифференциальных уравнений
- •5.3.Матричная форма решения уравнений состояния динамических систем
- •Моделирование динамических систем с двумя накопителями энергии при параметрических возмущениях Для определенности рассмотрим модель динамической системы с двумя накопителями энергии:
- •Моделирование –цепей. Аналитические решения
- •Сопротивления ,
- •Переходный процесс в -цепи под воздействием синусоидального входного сигнала
- •Системы, находящиеся под воздействием периодических сигналов прямоугольной формы
- •Динамические системы с двумя накопителями энергии
- •Корни комплексно-сопряженные.
- •Кратные корни.
- •Вещественные неравные корни
- •Динамические системы с тремя накопителями энергии
- •6. Моделирование динамических систем и электрических цепей средствами символьной математики
- •6.1. Символьные выражения и алгебра
- •6.2. Алгебраические и трансцендентные уравнения. Расчет цепи постоянного тока
- •Символьной алгебры
- •6.3. Символьное дифференцирование и интегрирование
- •6.4. Решение дифференциальных уравнений в символьной форме
- •6.5. Моделирование переходных процессов в электрических цепях средствами пакета символьной математики
- •6.6. Операторный метод расчета переходных процессов с использованием пакета символьной математики
- •7. Модели детерминированного хаоса и их применение
- •7.1. Дискретные динамические модели первого порядка со сложной динамикой
- •7.2. Программное обеспечение и моделирование нелинейных дискретных систем. Хаос
- •7.3. О применении нелинейных моделей систем для получения псевдослучайных хаотических последовательностей
- •Моделирование технологических процессов в системах с помощью нейронных сетей
- •8.1.Общие положения
- •8.2. Последовательность операций при создании нейронной сети в среде matlab ( Neural Networks Toolbox)
- •3. Оценка погрешности нейронной модели. Для оценки используется функция моделирования, где в скобках, согласно синтаксису, приводятся сеть и входной сигнал:
- •Моделирование уровней воды в водной коммуникации на основе нейронных сетей
- •В водной коммуникации
- •8.4. Применение нейронной сети для определения химического состава песчано – гравийной смеси
- •Моделирование технологического процесса оценки и прогноза рыночных факторов, воздействующих на работу предприятия и бизнес в классе нейронных сетей
- •Библиографический список
- •Оценка параметров, моделирование динамических систем и электрических цепей в среде MatLab
- •165300, Г. Котлас, ул. Невского, 20.
-
Динамические системы с двумя накопителями энергии
Для динамических
систем, содержащих одну массу и одну
пружину (аналогично – в электрических
цепях – индуктивность и емкость) и
находящихся под действием постоянной
силы (постоянной ЭДС источника
электроэнергии), можно предложить
решения в аналитическом виде. Действительно,
при наличии двух накопителей электроэнергии
матрицы в уравнении (5.48) можно записать:
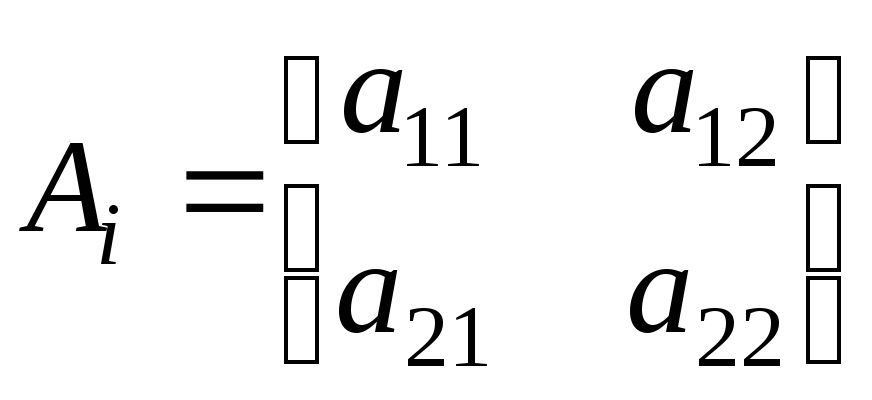 ,
,
![]() .
.
Сила, воздействующая
на систему,
![]() на интервале
на интервале
![]() приводит к изменению переменных состояния
– перемещения и скорости тела. Если
приводит к изменению переменных состояния
– перемещения и скорости тела. Если
![]() и вектор начальных условий (на левой
границе) равен
и вектор начальных условий (на левой
границе) равен
![]() ,
то поведение динамической системы будет
зависеть от корней характеристического
уравнения (собственных значений матрицы
,
то поведение динамической системы будет
зависеть от корней характеристического
уравнения (собственных значений матрицы
![]() ).
).
Корни комплексно-сопряженные.
Это условие выполняется при таких численных значениях элементов матрицы, которые отвечают неравенству:
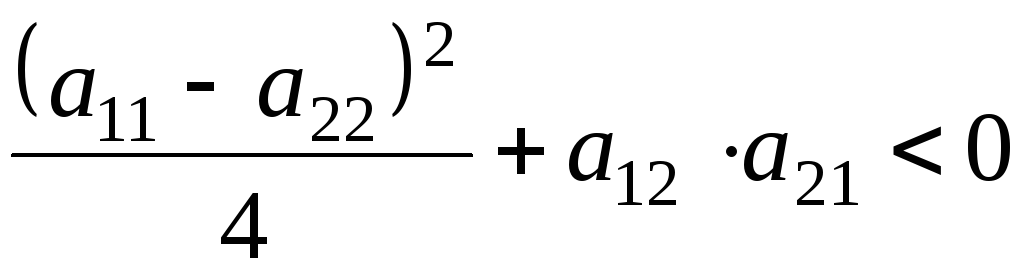 , (5.0)
, (5.0)
поскольку собственные значения
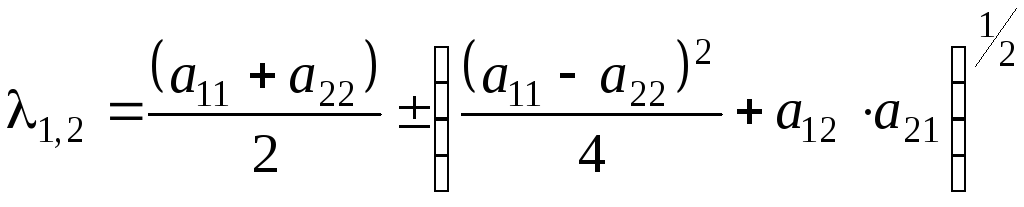 (5.0)
(5.0)
Неравенство (5.51) характеризует малый уровень диссипации (рассеяния) энергии, что приводит к появлению колебательных режимов в электрических цепях и динамических системах.
Искомые переменные состояния определим с помощью следующих зависимостей:
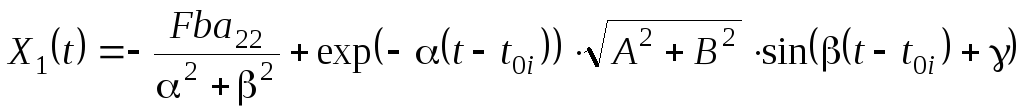 (5.0)
(5.0)
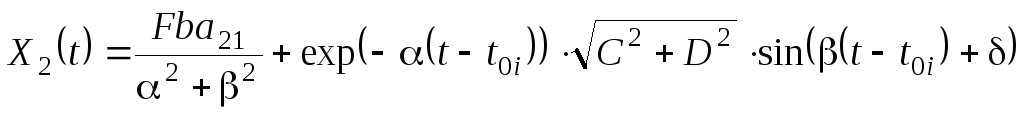 (5.0)
(5.0)
В уравнениях (5.535.54) расчетные коэффициенты находятся с помощью следующих соотношений:
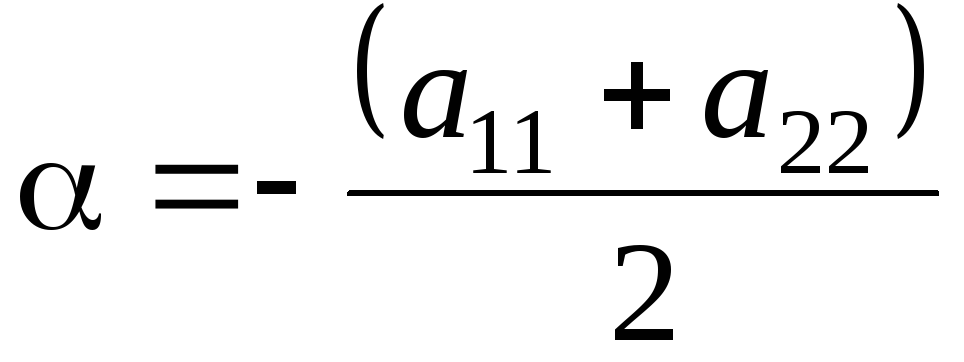 ;
;
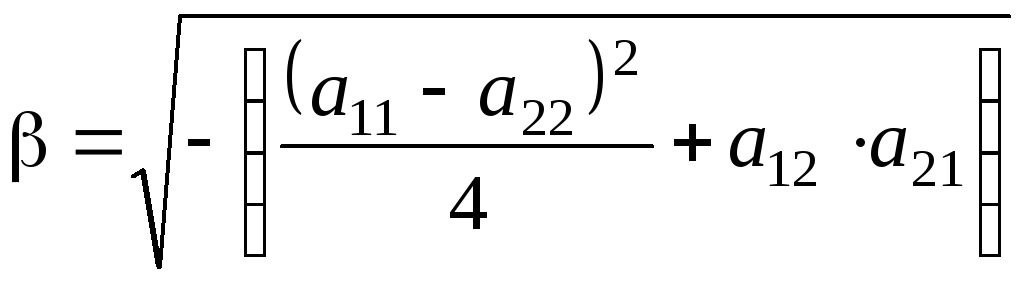 , (5.0)
, (5.0)
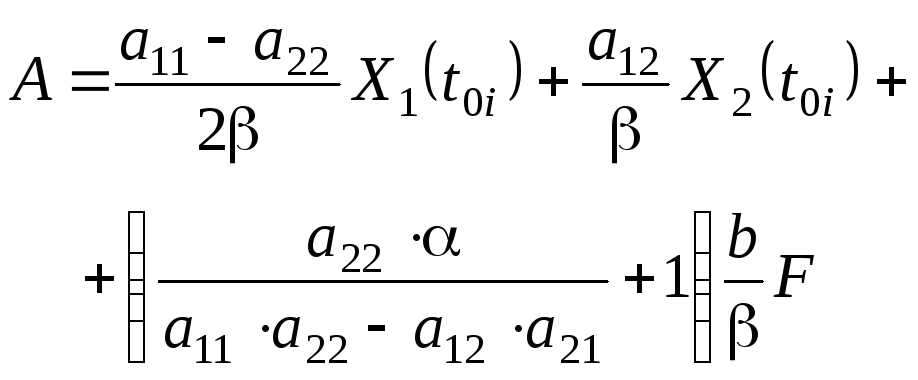 , (5.0)
, (5.0)
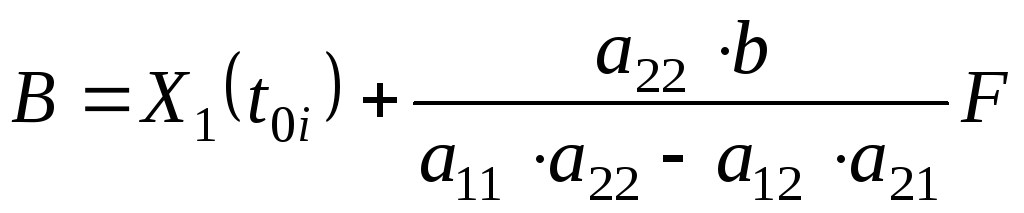 , (5.0)
, (5.0)
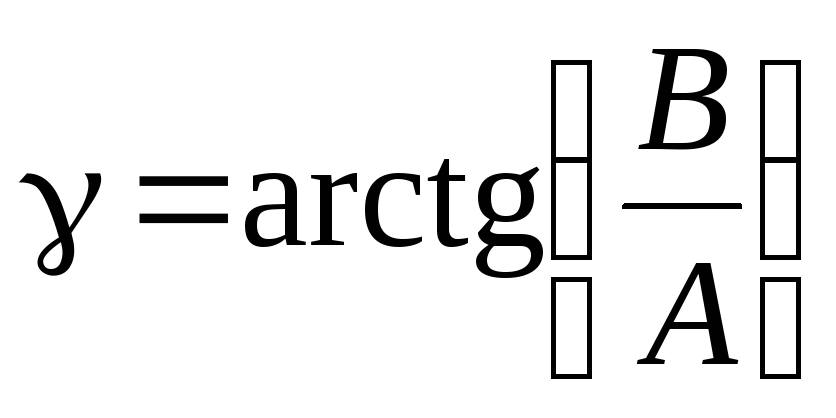 (5.0)
(5.0)
Нетрудно видеть,
что при
![]() аргумент
аргумент
![]() .
.
Коэффициенты, входящие в уравнение (5.54), вычисляются по формулам:
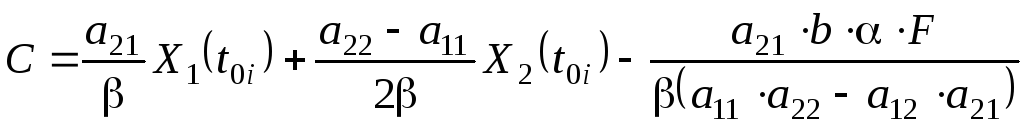 , (5.0)
, (5.0)
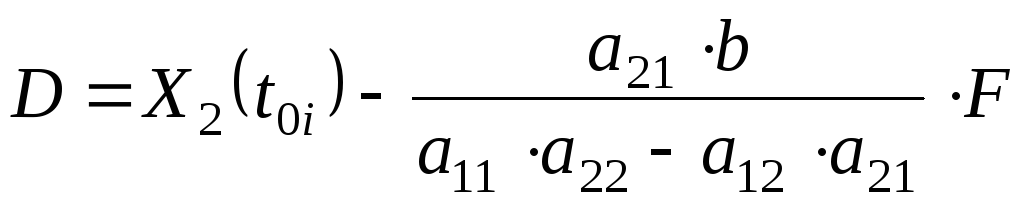 , (5.0)
, (5.0)
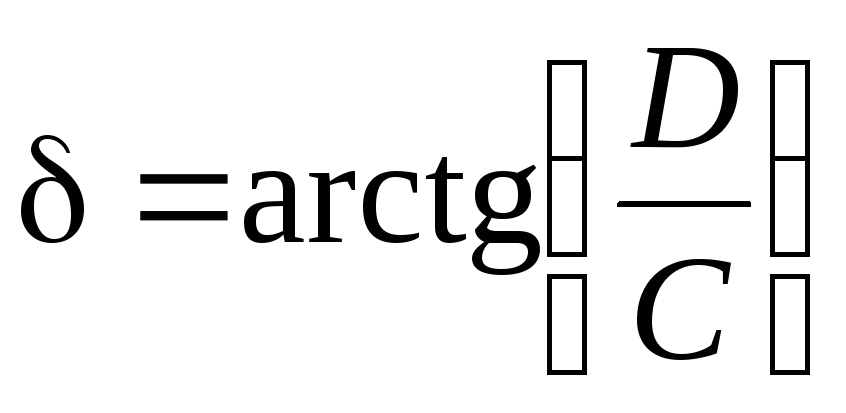 , (5.0)
, (5.0)
причем
![]() ,
если
,
если
![]() .
.
Кратные корни.
Из (5.52) следует,
что
![]() ,
если выражение под корнем равно нулю:
,
если выражение под корнем равно нулю:
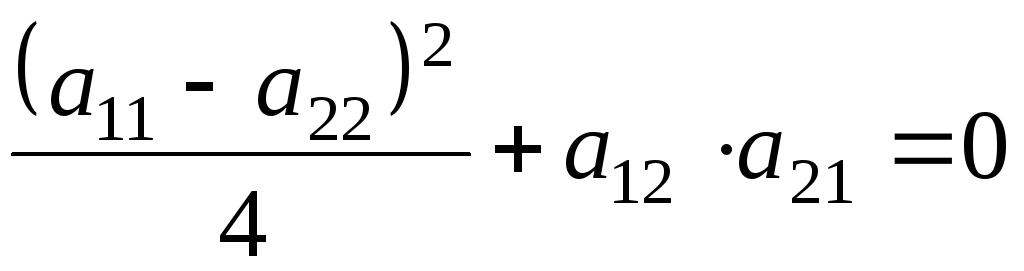 (5.0)
(5.0)
Режим, характеризуемый
равенством (5.62), может быть получен путем
изменения коэффициентов
![]() и
и
![]() (увеличение активного сопротивления в
электрической цепи, либо коэффициента
при первой производной в дифференциальном
уравнении динамической системы второго
порядка). На практике этот режим
встречается достаточно редко. Однако,
решения уравнений для этого режима
также полезно привести:
(увеличение активного сопротивления в
электрической цепи, либо коэффициента
при первой производной в дифференциальном
уравнении динамической системы второго
порядка). На практике этот режим
встречается достаточно редко. Однако,
решения уравнений для этого режима
также полезно привести:
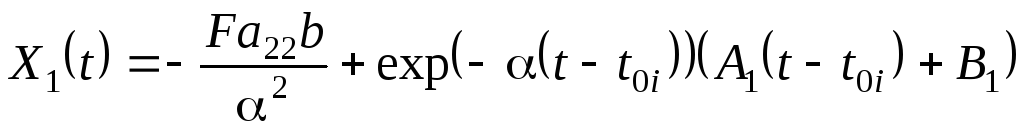 (5.0)
(5.0)
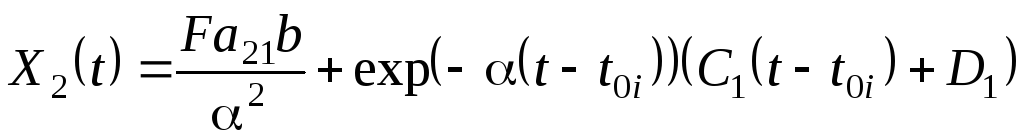 (5.0)
(5.0)
В уравнениях (5.63)
и (5.64) коэффициенты
![]() ,
,
![]() ,
,
![]() и
и
![]() вычисляются по следующим формулам:
вычисляются по следующим формулам:
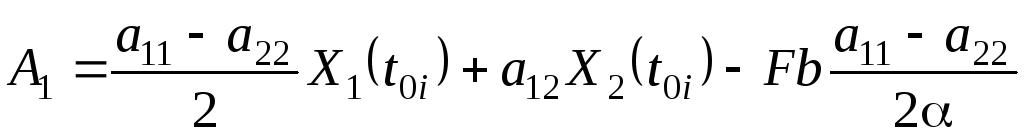 (5.0)
(5.0)
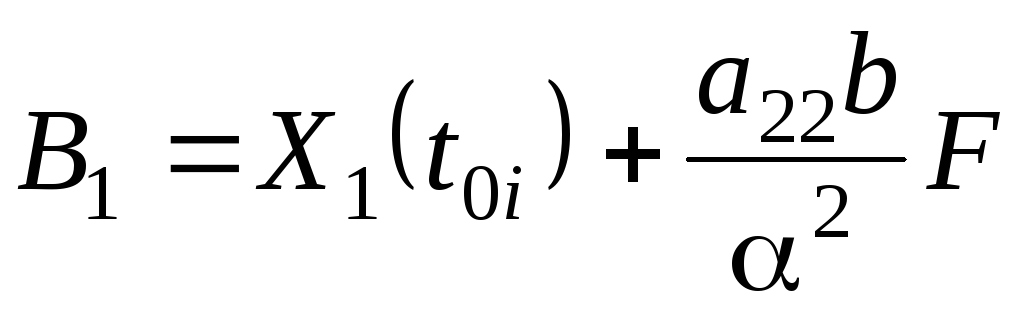 (5.0)
(5.0)
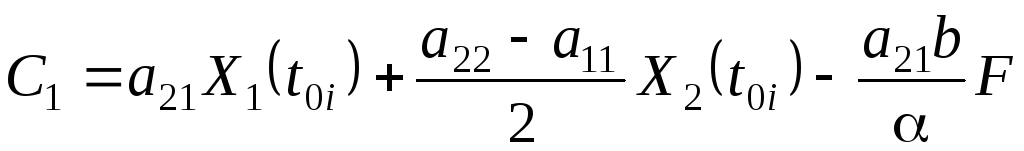 (5.0)
(5.0)
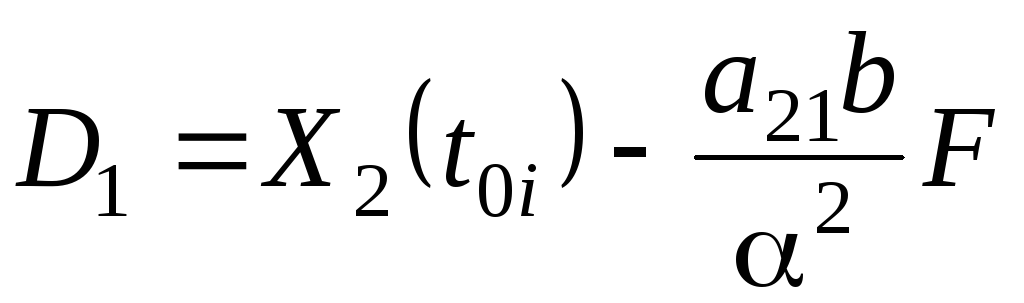 (5.0)
(5.0)
Параметр
![]() определяется, как и ранее, с помощью
уравнения (5.55).
определяется, как и ранее, с помощью
уравнения (5.55).
Вещественные неравные корни
Дальнейшее увеличение рассеяния энергии в системе ведет к тому, что:
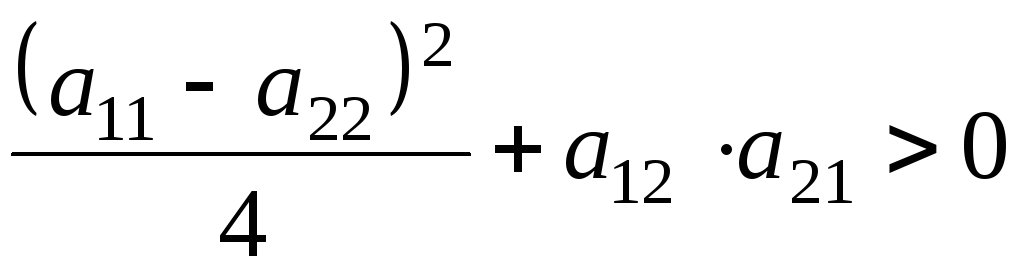 , (5.0)
, (5.0)
собственные
значения матрицы
![]() становятся вещественными и различными,
а переходный процесс – апериодическим.
Для расчета переменных состояния можно
использовать следующие зависимости:
становятся вещественными и различными,
а переходный процесс – апериодическим.
Для расчета переменных состояния можно
использовать следующие зависимости:
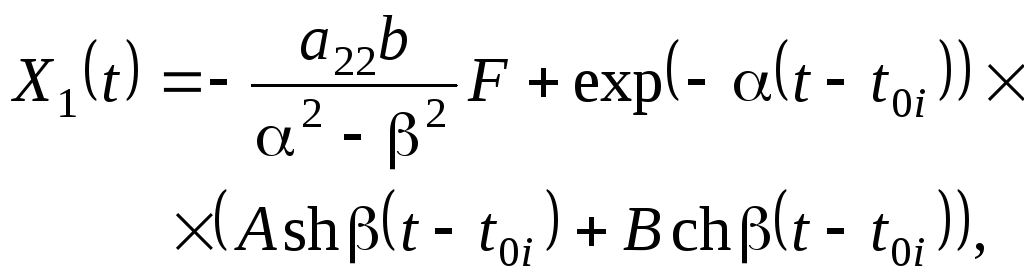 (5.0)
(5.0)
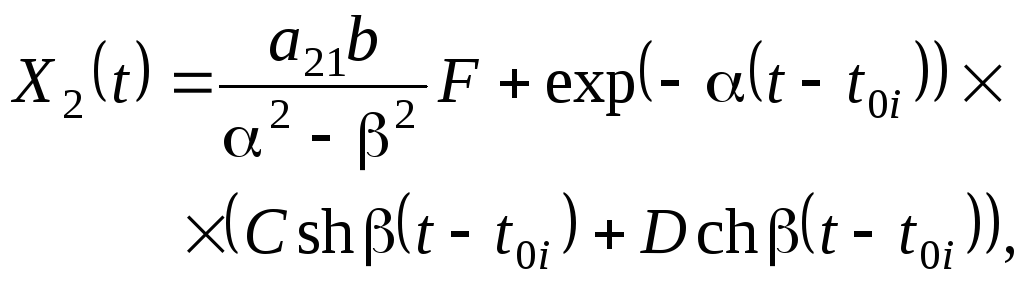 (5.0)
(5.0)
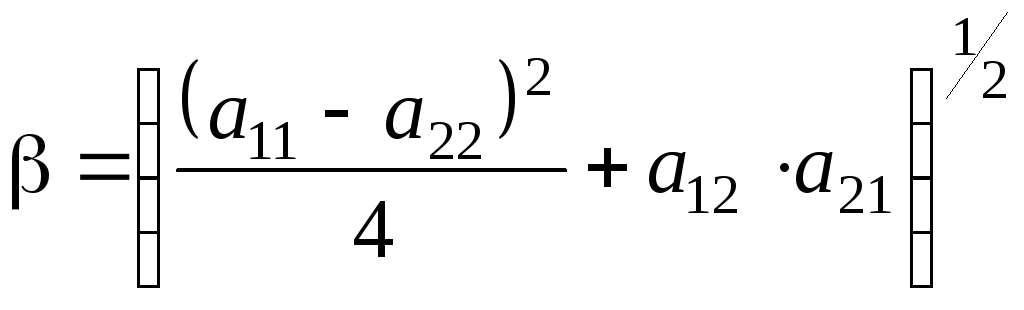 (5.0)
(5.0)
Коэффициенты
![]() ,
,
![]() ,
,
![]() ,
,
![]() и
и
![]() определяются с помощью ранее приведенных
уравнений (5.555.60).
Для справки напомним, что гиперболический
синус и косинус вычисляются с помощью
экспонент:
определяются с помощью ранее приведенных
уравнений (5.555.60).
Для справки напомним, что гиперболический
синус и косинус вычисляются с помощью
экспонент:
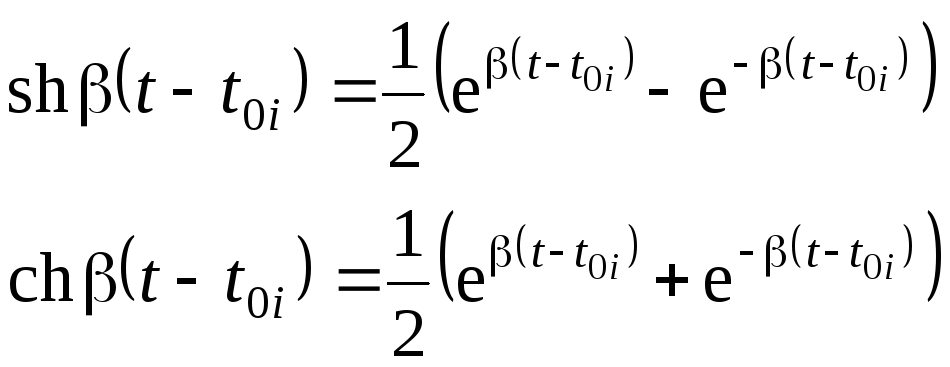 .
.
Полученные
зависимости (5.515.72)
приведены для расчета переходного
процесса на
![]() -ом
участке (временном интервале). Исходными
данными для расчета на
-ом
участке (временном интервале). Исходными
данными для расчета на
![]() -ом
интервале должны быть, естественно,
соответствующие
-ом
интервале должны быть, естественно,
соответствующие
![]() ,
,
![]() и сила
и сила
![]() ,
а также
,
а также
![]() .
.
При
этом начальные условия должны быть
равны конечным условиям на
![]() -ом
интервале:
-ом
интервале:
![]() и
и
![]() .
.
Отметим также, что полученные формулы могут быть легко запрограммированы, а выбор одной из трех групп формул для расчета может быть произведен по результатам оценки, выполненной с помощью соотношений (5.51), (5.62) и (5.69).
