4. Моделирование –цепей. Аналитические решения

В четвертой главе была рассмотрена процедура составления дифференциальных уравнений путем приведения исходной -цепи к резистивной форме. Возвратимся теперь к электрической цепи, изображенной на рис. 5.11 а) и остановимся на решении дифференциальных уравнений, используя матричный метод анализа переходных процессов.

В ектор состояния содержит две составляющие: ток и напряжение , то есть: .

Уравнения динамики цепи имеют вид:

, (5.0)

где – ЭДС источника электроэнергии,

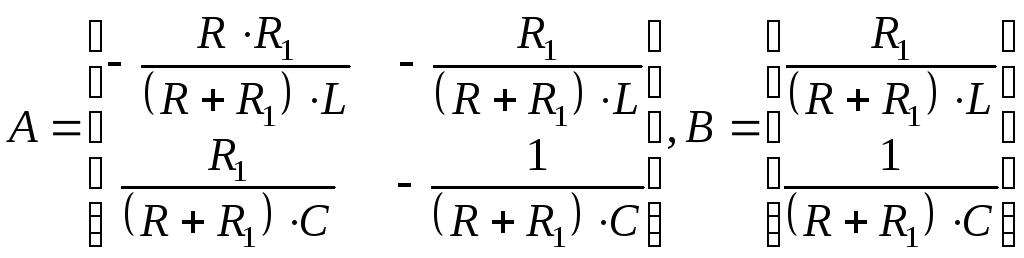(5.0)

Поведение -цепи зависит от собственных чисел матрицы , которые мы можем изменять путем вариации значений активных сопротивлений, индуктивности и емкости.

Рассмотрим несколько частных случаев.

1. Сопротивления ,

Элементы матриц уравнения (5.23) принимают следующие значения:

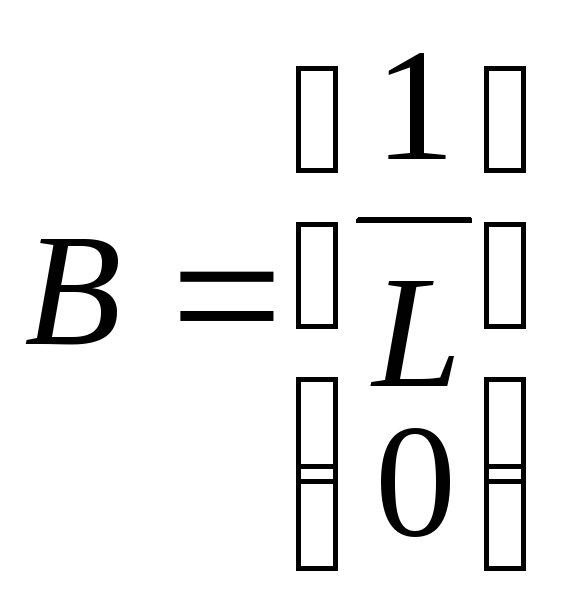, (5.0)

Электрическая цепь становится неразветвленной, состоящей из последовательно соединенных и (рис. 5.11 б)).

Поскольку активные сопротивления в цепи отсутствуют, динамическая система становится консервативной, и теоретически переходный процесс должен протекать без рассеяния (потерь) энергии.

До замыкания ключа ток через индуктивность и напряжение на емкости равны нулю. Следовательно, вектор начальных условий .

Для определения характеристического уравнения системы (5.22) составим определитель (детерминант) матрицы:

(5.0)

Поскольку собственные значения матрицы численно совпадают с корнями характеристического уравнения (5.25), то они равны: 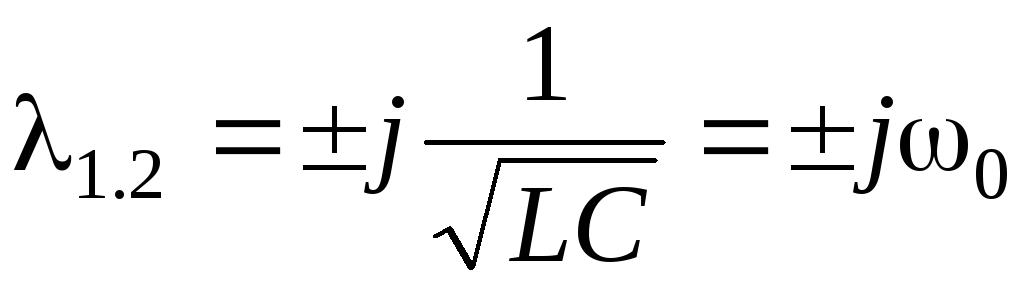, где – собственная частота цепи (рис. 5.11 б)).

Для удобства проведения математических преобразований воспользуемся операторным методом. Применение операторного метода позволяет в области изображений (частотной области) обращаться с матричным дифференциальным уравнением как с алгебраическим.

Процедура решения состоит в следующем. Сначала с помощью таблиц преобразований Лапласа осуществляется операция перевода дифференциального уравнения из области оригиналов (временная область) в область изображений (частотная область). Затем выполняются решения алгебраического уравнения в частотной области относительно вектора состояния, записанного в операторной форме. На последнем этапе также с помощью таблиц преобразований Лапласа производится переход от алгебраического уравнения в частотной области к уравнению во временной области (переход из области изображений в область оригиналов). Все данные таблиц преобразований Лапласа в среде MatLAB можно найти в приложении Symbolic Toolbox - пакете символьной математики [20].

При нулевых начальных условиях переход в область изображений для слагаемых уравнения (5.22) будет заключаться в использовании следующих данных:

, , , (5.0)

где – оператор Лапласа, есть знак соответствия между выражениями во временной области (слева от знака) и частотной области (справа от знака).

С учетом (5.26) получим операторную форму записи матричного дифференциального уравнения (5.22):

(5.0)

Обращаясь с формулой (5.27) как с алгебраическим матричным уравнением, мы вправе записать: .

Его решение относительно вектора переменных состояния в операторной форме:

(5.0)

С учетом (5.24) уравнение (5.28) примет вид:

(5.0)

Обратная матрица в уравнении (5.29) определится с помощью стандартной процедуры инверсии: , где – присоединенная для матрица, – определитель матрицы . В рассматриваемом случае инверсная матрица для :

.

Таким образом, в операторной форме ток через индуктивность:

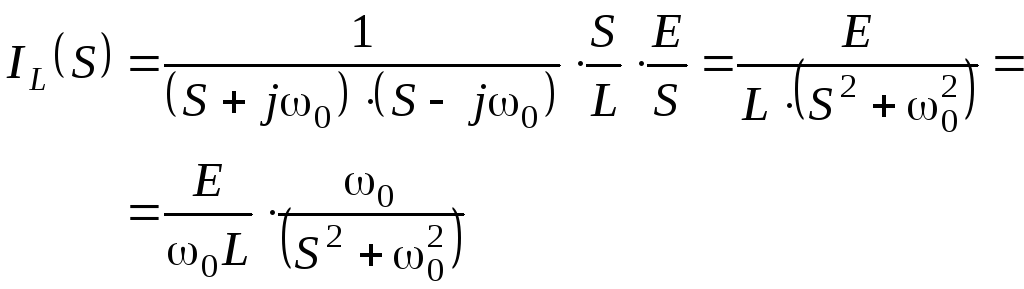(5.0)

Напомним, что согласно таблицам преобразований Лапласа, выполняется условие соответствия:

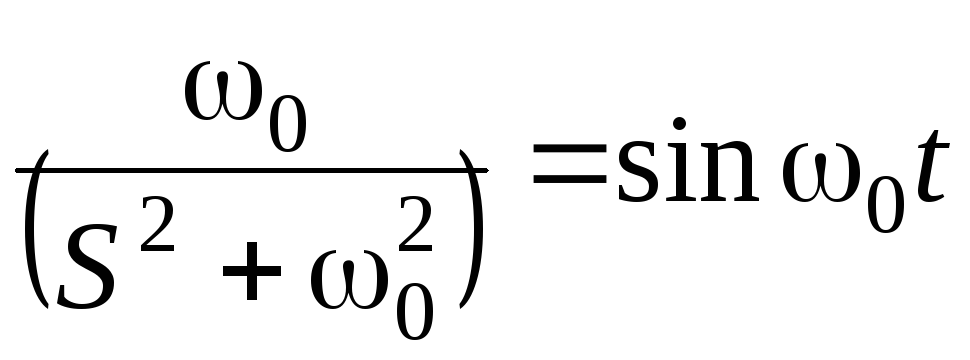
(5.0)

Воспользуемся этим соответствием для перехода из области изображений в область оригиналов. Току через индуктивность, определенному формулой (5.30), во временной области соответствует выражение:

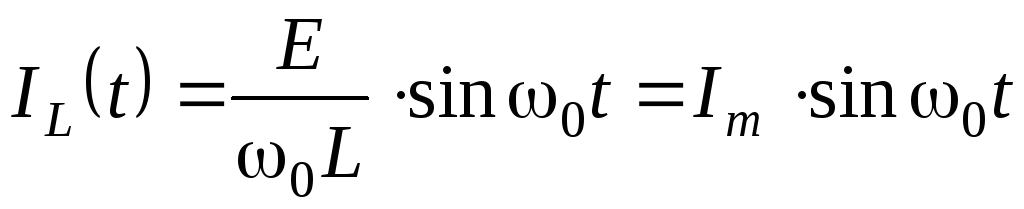, (5.0)

где 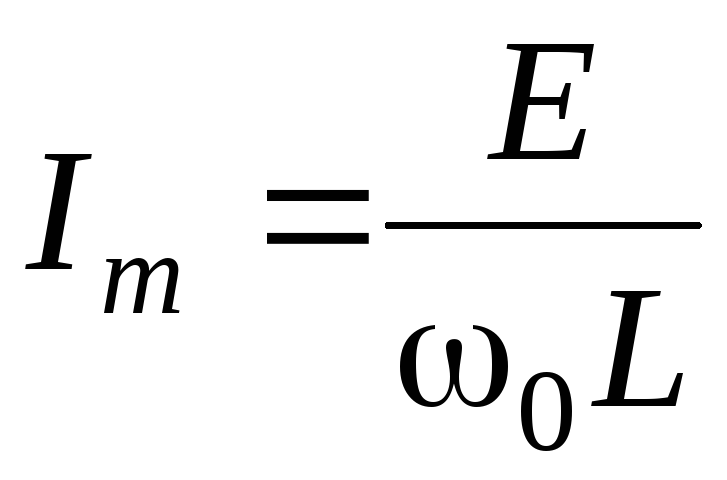– амплитуда тока. Таким образом, ток в электрической цепи изменяется по закону синуса.

Напряжение на емкости в операторной форме, согласно (5.29), равно:

. (5.0)

Из правил выполнения преобразований Лапласа известно, что интегрирование функции в области оригиналов (при нулевых начальных условиях) соответствует делению на оператор этой функции в области изображений. Обращаясь вновь к уравнению (5.33) и соответствию (5.31), мы видим, что в знаменателе (5.33) содержится оператор . Следовательно, выражение в частотной области соответствует интегралу правой части (5.31) во временной области.

Поэтому для напряжения на емкости как функции времени имеем: , где – постоянная интегрирования, определяемая из начальных условий. Действительно, напряжение . Тогда постоянная интегрирования .

Подставляя это выражение в записанное выше выражение для , мы получим:

. (5.0)

Напряжение на индуктивности определим по формуле:

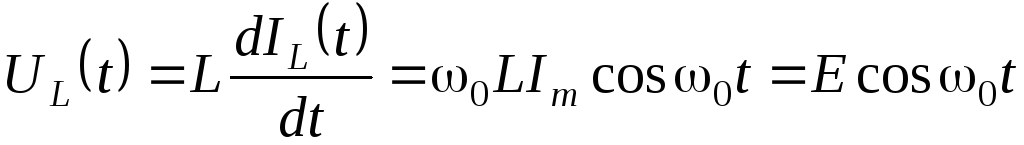. (5.0)

Для наглядного представления кривых, определяемых формулами (5.32), (5.34) и (5.35), построим графики с помощью MatLAB и выведем их на печать. Составим программу, представленную файлом .

Программа содержит текстовые комментарии, которые начинаются со знака «%». Затем задается вектор времени , изменяющийся от 0 до 6 (при шаге дискретности ). Принятые расчетные значения: ; . Построение графиков выполняется оператором . По окончании построения графиков оператором задается пауза. Обратите внимание на то, что все вычисления производятся в процессе выполнения оператора .

Файл

%File “sah36.m”.

%Plots for electrical system.

%LC-circuit with DC source

Im=0.5; E=2;

x=0:0.02*pi:6.0*pi;

subplot(221);

plot(x, Im*sin(x), x, E*(1-cos(x)), x, E*cos(x)), grid

pause

Графические построения приведены на рис.5.12.

Из приведенных графиков следует, что кривая напряжения на емкости располагается выше оси абсцисс (то есть не принимает отрицательных значений). Напряжение имеет постоянную составляющую и составляющую , изменяющуюся с собственной частотой . В любой момент времени сумма напряжений на емкости и индуктивности равна постоянному значению, равному , что отвечает закону Кирхгофа: