1. Краткие сведения о решателях дифференциальных уравнений

Для решения обыкновенных дифференциальных уравнений с заданными начальными условиями (задачи Коши) в системе MatLAB используются функции-решатели. Они позволяют пользователю выбирать метод решения, вводить начальные условия и назначать специальные опции для повышения информативности выполняемых вычислительных операций .

Решение дифференциальных уравнений обычно производится с помощью функций класса ОDE, номера которых выбираются в зависимости от назначения [34]:

функция ОDE45 – наиболее употребляемая, порядок метода – переменный;

функция ОDE23 – используется при низких требованиях к точности;

функция ОDE23S –применяется при низких требованиях к точности и необходимости решения систем уравнений в неявной форме Коши (например, в виде M*dx/dt=F(x,t); явная форма имеет структуру dx/dt=f(x,t) );

функция ОDE23t – если допустима умеренная точность и если решаются осцилляционные задачи без демпфирования;

функция ОDE23tb – при низких требованиях к точности решения уравнений в неявной форме Коши с нестационарной матрицей при производных;

функция ОDE113 – при высоких требованиях к точности и решении уравнений со сложными правыми частями.

Синтаксис функции:

[t,x,s]=ode45(‘файл-функция’,[t0 tf],x0)

Здесь [t0 tf] –временной интервал интегрирования,

x0 – вектор- столбец начальных условий,

t – текущее время ( выводимое на каждом шаге интегрирования);

x – вектор переменных состояний;

s – сведения о ходе вычислений (при выводе расчетных данных может не использоваться).

В средах MatLAB последних версий содержатся операторы, предназначенные для решения двухточечных граничных задач.

В каждом файле содержится программа, предназначенная для численного интегрирования дифференциальных уравнений методом Рунге-Кутта. Программой предусматривается автоматический выбор шага интегрирования. Для решения задач с использованием решателя необходимо знать начальное время интегрирования, конечное время интегрирования, вектор начальных условий, а в строке, выполняющей процедуру интегрирования, – в скобках указать файл- функцию, где содержатся дифференциальные уравнения модели динамики системы. Если требуется вывести на дисплей решение в графической форме, необходимо заполнить правильно строки с оператором .

Поясним описанную процедуру на примере интегрирования линейного дифференциального уравнения с двумя накопителями энергии.

Предположим, что необходимо определить переходный процесс в динамической системе, описываемой матричным уравнением:

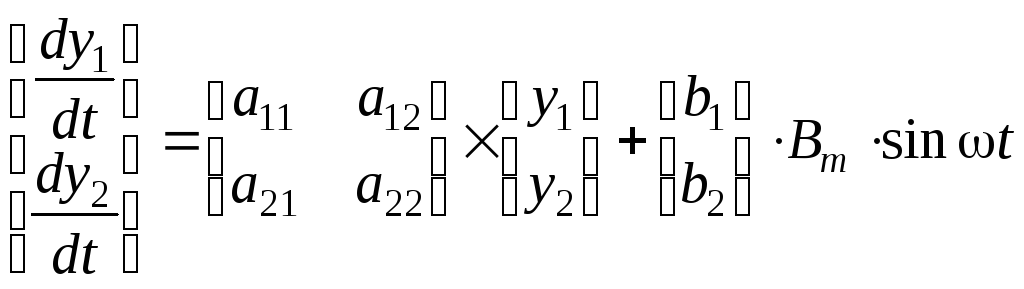, (5.0)

где для определенности примем следующие значения постоянных коэффициентов и элементов матриц:

(5.0)

Вектор начальных условий , время интегрирования . Заданная погрешность интегрирования не указана (по умолчанию ).

Собственные значения матрицы являются комплексно-сопряжен­ными числами с отрицательной вещественной частью: .

Решение задачи выполняется с помощью двух программ, представленных файлами и . Первая программа является основной, а вторая – вспомогательной (файл-функцией), служащей для записи правой части уравнения (5.1) со значениями коэффициентов, соответствующими данным (5.2).

Файл «MMM.M»

%Investigation of the second-order dynamical systems.

%The main file ‘mmm.m’ and the complementary file ‘sah2.m’.

echo off

clc

%To simulate a system, we create a function M-file that returns

%state derivatives. Given state and time values. For this example,

%we’ve created a file called SAH2.M. Here’s what it looks like:

R=[0 1; -1 0]

eig(R)

pause %Strike any key to continue.

сlc

%To simulate the differential equation defined in SAH2 over the

%interval 0<t<20, we invoke ODE23:

t0=0;

tfinal=40;

y0=[2.5 12.5]’; %Define initial conditions.

%[t, y]=ode23(‘sah2’, t0, tfinal, y0):

pause %Strike any key to start ODE23 solution.

tol=1.e-3; %Accuracy

trace=-2.2;

[t, y]=ode23(‘sah2’, t0, tfinal, y0, tol, trace);

plot(t, y), title (‘Second-order equation time history’), grid,

pause

plot(y(:,1),y(:,2)), title(‘Second-order equation - phase plane plot’),

grid,

pause

Файл «SAH2.M»

%File ‘sah2.m’.

%The behavior of dynamical system (electrical circuits model).

%Two energy capacitance.

function yprime=sah2(t, y);

%This program is auxiliary and implemented with the

%main program (file ‘mmm.m’).

%Matrix coefficients: a11=0, a12=-1, a21=1, a22=-0.2

yprime=[0 –1; 1 –0.2]*[y(1) y(2)]’+[1 0]’*4*sin(3*t);

Остановимся кратко сначала на описании . Комментарии к программе содержатся в строках, начинающихся со знака «%». Рабочая часть файла представляется лишь двумя строками – четвертой и восьмой. Четвертая строка содержит оператор (функция) и синтаксическое определение этой функции. Функция с именем является функцией времени и вектора .

Уравнение (5.1) в векторной форме записано в последней (восьмой) строке. После знака равенства, стоящего за функцией , записана матрица , которая умножена на вектор-столбец (обратите внимание на знак транспонирования). К этой части уравнения добавляется (в виде суммы) второе слагаемое матричного уравнения, представляющее собой воздействие внешнего синусоидального сигнала на динамическую систему. Вспомогательная программа должна быть обязательно записана в файл , к которому в процессе решения периодически будет обращаться основной файл .

Основной файл , также содержит комментарии, следующие за каждым знаком «%» в соответствующих строках, и операторы, обеспечивающие выполнение следующих операций:

– оператор, отключающий режим отображения листинга на дисплей;

– очищает экран от записей, содержащихся на нем.

В программе используется также операция , позволяющая определить собственные значения матрицы . После вывода результата вычислений на экран устанавливается пауза . Далее следуют строки с заданным начальным временем интегрирования , конечным временем и вектором начальных условий . Обратите также внимание на то, что представляет собой вектор-столбец.

Интегрирование выполняется решателем , при записи которого в круглых скобках указываются данные, используемые в процессе расчета. Здесь содержится файл (расширение не указывается), а также численные значения других параметров, определяющих режим работы внешнего файла. По завершении расчетов на дисплей с помощью оператора выводятся зависимости и как функции времени, а оператор служит для нанесения координатной сетки из пунктирных линий. Чтобы изображение не исчезло с экрана, мы используем оператор . Наконец, после нажатия клавиши <Enter> получим изображение процесса на фазовой плоскости, где по оси отложена переменная , а по оси – переменная .

Решение дифференциального уравнения во временной области представлено на рис. 5.1, а на фазовой плоскости – на рис. 5.2. В процессе анализа кривых, приведенных на рис. 5.1, рекомендуется обратить внимание на выполнение начальных условий в момент , а также на то, что с течением времени переходный процесс затухает, и колебания стремятся к вынужденным составляющим, определяемым синусоидальным сигналом от внешнего источника.

В изображении фазового портрета особый интерес представляет область, характеризуемая наложением собственных затухающих колебаний на вынужденные колебания системы.

Чтобы внести новые коррективы в модель системы, необходимо войти в редактор, вызвать файл , в последней строке программы записать требуемые значения элементов матриц состояния и управления, а также параметры сигнала внешнего источника (частоту, амплитуду, фазу). Затем надо произвести запись откорректированной программы в тот же файл, либо в другой (если необходимо сохранить исходный). Затем следует с помощью редактора открыть файл и также внести коррективы, изменив время интегрирования (в зависимости от собственных значений матрицы ), ошибку интегрирования, начальные условия и др. Необходимо, в случае изменения наименования вспомогательного файла, указать его в строке содержащей . Затем записать откорректированную программу в файл под исходным, либо новым именем (обязательно с расширением ). Выход из редактора и вход в систему MatLAB может осуществляться любым из способов, принятых пользователем для работы. Для расчетов по программе необходимо набрать на экране монитора наименование файла (без расширения), либо вызвать иной основной файл с принятым именем.

Следует иметь ввиду, что по завершении вычислений все расчетные результаты сохраняются. Можно в режиме прямых вычислений вывести их на экран в той форме, которая необходима. Сначала можно определить размерность вектора или матрицы с помощью функции . При нажатии клавиши <Enter> на экране появятся два числа. Теперь можно вывести на экран любой вектор, либо его часть. Например, с помощью оператора на экране отображаются строки с 21 по 40-ю в виде двух столбцов. В первом столбце будут содержаться расчетные данные вектора , а во втором .

В процессе вычислений по программе можно образовать матрицу, содержащую в первом столбце время, а во втором и третьем – переменные состояния, а затем вывести данные вычислений на экран и на печать. Все эти операции выполняются в системе MatLAB исключительно просто, а главное – в режиме прямых вычислений.

Если возникает необходимость определения данных по графикам, можно изменить масштабы по осям , и вывести только ту часть графических изображений, которая представляет интерес в данном конкретном случае.

Программа предназначена также для интегрирования дифференциальных уравнений. Она обеспечивает меньшую погрешность вычислений (в сравнении с ) за счет использования улучшенной процедуры Рунге-Кутта.

В процессе моделирования переходных режимов мы предполагаем возвращение к программам типа и . Поэтому описание некоторых деталей работы с программами будет дано в последующих параграфах.