4.4. Определение коэффициентов дифференциальных уравнений моделей электрических цепей с двумя накопителями энергии

Предположим, что электрическая цепь содержит одну емкость, одну индуктивность, любое число активных сопротивлений и один источник постоянной ЭДС, к которому подключается цепь. Возвращаясь к общей модели (4.10), мы можем утверждать, что уравнения динамики цепи есть два линейных дифференциальных уравнения:

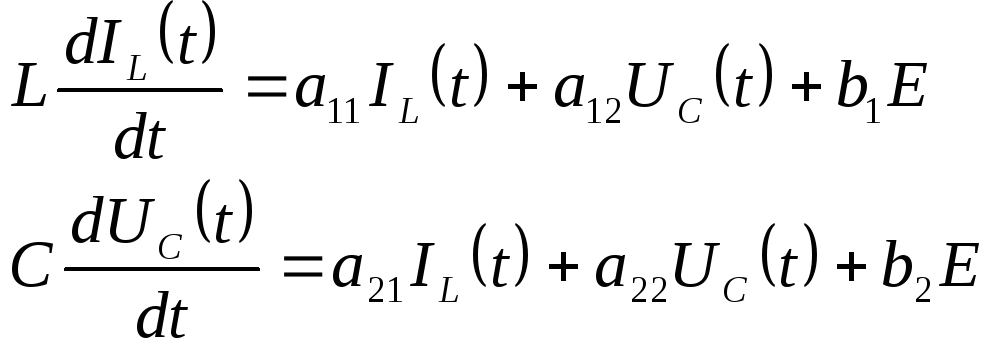(4.25)

Постоянные коэффициенты этих уравнений также могут быть опре­делены непосредственно из резистивной формы цепи.

Рассмотрим процедуру вычисления коэффициентов на примере раз­ветвленной цепи, приведенной на рис. (4.5 а). Переменными состояния це­пи являются ток через индуктивность I_L(t) и напряжение на емкости U_С (t). В момент t = 0₊, когда ключ k замкнут, согласно ранее изложен­ным правилам, можно составить резистивную цепь (рис.4.5 б), где емкость заменена источником ЭДС, а индуктивность - источником тока. Связи ме­жду переменными в этой цепи определяются двумя алгебраическими уравнениями, которые можно записать в приращениях на основании (4.25):

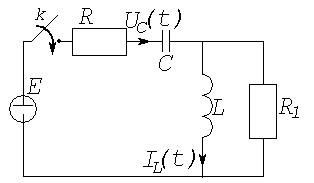
а) б)

Рис. 4.5. RLC – цепь и ее резистивная форма

(4.26)

Рассмотрев примеры, приведенные в параграфе 4.3, мы можем не со­ставлять отдельно цепи для определения каждого коэффициента. Необхо­димо лишь условно учесть внутренние сопротивления «замороженных» источников тока и ЭДС. Чтобы найти a₁₁, мы полагаем, что под действием источника тока , который протекает по двум параллельно соеди­ненным сопротивлениям R и R₁ (входное cсопротивление резистивной цепи по клеммам 12), напряжение источника тока уменьшится на величину , то есть на величину падения напряжения на этих сопротивлениях. Уменьшение означает необходимость использовать коэффициент пропорциональности со знаком «-». Поэтому .

Под действием в цепи должен протекать ток по двум по­следовательно соединенным резисторам R и R₁. Внутреннее сопротивле­ние источника тока, расположенного между клеммами 1 и 2, равно беско­нечности. При этом, с учетом принятого направления тока, напряжение на индуктивности уменьшится на величину падения напряжения на сопротивлении R₁: .

В результате получим

Источник ЭДС , воздействуя на резистивную цепь, вызовет увеличение напряжения на клеммах 1 и 2: .

Следовательно, коэффициент b₁ равен:

Чтобы найти a₂₁ мы должны определить ток в левой ветви цепи, ес­ли он генерируется источником . Так как распределяется по ветвям обратно пропорционально их сопротивлениям, то получим:

.

Этот ток совпадает по направлению с I_C . Следовательно, коэффици­ент пропорциональности должен записываться со знаком «+»

.

Коэффициент а₂₂, характеризующий влияние напряжения (0₊) на ток через этот источник, равный (0₊), определим следующим обра­зом. Ток в цепи направлен встречно I_C, поэтому знак коэффициента отри­цательный. Величина тока: .

Наконец, под действием (0₊) в цепи появляется ток, направлен­ный согласно с током I_C , а его величина находится по закону Ома: .

Поэтому

Подставим найденные коэффициенты в уравнения (4.25) и приведем их к виду, определенному моделью пространства состояний. В векторно-матричной форме модель имеет вид:

(4.27)

Конечно, уравнение (4.27) можно получить с помощью законов Кирхгофа, либо любым иным методом, применимым для расчета электри­ческих цепей. Однако в целом ряде случаев метод приведения цепей к резистивной форме может обеспечить экономию времени, необходимого для выполнения математических преобразований. Эффективность метода особенно заметна при работе с цепями, содержащими большое число реактив­ных элементов и источников питания. По крайней мере, его можно применять параллельно с другими методами для проверки правильности выполненных преобразований.