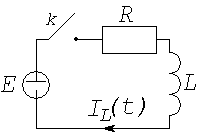
4.3. Приведение к резистивной форме моделей электрических цепей с одним накопителем энергии

Рассмотрим электрическую цепь, изображенную на (рис. 4.2).

В момент коммутации (при замыкании ключа «k»), согласно первому закону коммутации, ток в цепи мгновенно изменяться не может. Поэтому в момент t=0₊ ток в цепи , и напряжение источника уравновешивается напряжением на индуктивности.

Согласно правилам, изложенным в предыдущем параграфе, заменим индуктивность источником тока.

а) б)

в) г)

Рис. 4.2. RL – цепь и ее резистивная форма

Обозначим этот ток (рис. 4.2 б). Цепь содержит один накопитель энергии (индуктивность) и один источник ЭДС (внутреннее сопротивление источника ЭДС равно нулю). Поэтому, согласно (4.10), динамическая модель цепи может быть представлена уравнением [23]:

(4.13)

Заметим, что эта модель справедлива также для любой разветвлен­ной цепи, содержащей только одну индуктивность и один источник элек­троэнергии (например, источник тока). Однако выражения для коэффициентов а и b бу­дут отличаться, поскольку они определяются топологией конкретной цепи.

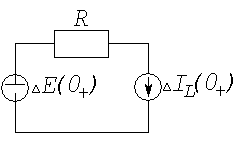
Цепь, изображенная на (рис. 4.2 б), приемлема только для момента t = 0₊ при условии, что изменяется скачком. Она не содержит инерционных элементов. Поэтому (1.3-1) можно заменить алгебраическим уравнением:

(4.14)

Постоянный коэффициент а в уравнении (4.14) определяет приращение напря­жения на индуктивности при изменении (скачком) тока , а коэф­фициент b - приращение напряжения на индуктивности при изменении ЭДС источника на величину.

Используя принцип суперпозиции (наложения), мы можем искусст­венно вводить лишь приращение одной переменной, а вторую при этом «замораживать». Например,

, (4.15)

. (4.16)

Для удобства определения неизвестных коэффициентов приращения переменных можно принять равными единице. Если увеличение тока на одну единицу (например, на 1 Ампер) будет приводить к уменьшению напряжения на индуктивности на величину , то ко­эффициент а должен приниматься со знаком «минус», а если к увеличе­нию - со знаком «плюс». Аналогично определяется знак коэффициента b.

Согласно (4.15), «заморожено». Поэтому в резистивной форме цепи (рис.4.2 в) источник ЭДС отсутствует, однако сохранено его внутреннее сопротивление, равное нулю. Если в момент t = 0₊ с помощью источника тока генерировать скачком ток, это вызовет па­дение напряжения на сопротивлении R, равное . С учетом принятых на схеме знаков, напряжение на источнике тока уменьшится на величину . Следовательно, коэффициент а по модулю равен , а с учетом знака приращения напряжения, он должен быть принят со знаком «-», то есть а = - R.

Теперь остановимся на уравнении (4.16). В момент времени t = 0₊ ему соответствует резистивная цепь, приведенная на рис.4.2 г). Источник тока из цепи исключен, а его внутреннее сопротивление, равное бесконеч­ности, оставлено.

Заметим, что при изменении скачком (на 1 вольт) напряжения , оно будет полностью приложено к источнику тока (ток в цепи от­сутствует). С учетом знаков сигналов, напряжение на источнике тока возрастет до значения . Следовательно, коэффициент b = 1.

Дифференциальное уравнение (4.13), в отличие от алгебраического, позволяет описать процесс в любой момент времени 0₊  t < , в том чис­ле - в момент t = 0₊. Поэтому полученные коэффициенты могут быть пе­ренесены в (4.13). Тогда будем иметь:

(4.17)

Запись (4.17) в форме Коши:

(4.18)

показывает, что матрицы А и В модели (4.4) вырождаются в элементы

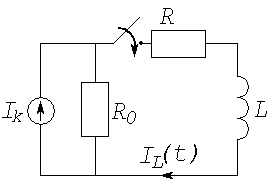
Рассмотрим цепь, содержащую одну индуктивность и источник тока (рис.4.3 а). Ее резистивная схема представлена на (рис. 4.3 б).

Модель цепи (рис.4.2) сохраняется, с учетом того, что источником элек­троэнергии является источник тока

(4.19)

а) б)

Рис.4.3. RL – цепь с источником тока и ее резистивная форма.

Для резистивной цепи (рис. 4.3 б) справедливо алгебраическое уравнение

(4.20)

Генерируя при , мы получим: и аналогично будем иметь .

Таким образом, динамическая модель цепи, определяемая (4.19), представляется дифференциальным уравнением

или в форме Коши:

(4.21)

На рис. (4.4 а) приведена RC-цепь, подключаемая к источнику по­стоянной ЭДС. Возвращаясь к (4.10), мы видим, что при наличии одного накопителя энергии (емкости) и одного источника, независимо от числа и схемы соединений активных сопротивлений, модель цепи должна иметь вид:

(4.22)

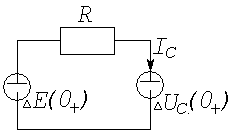
а) б)

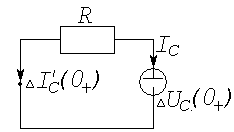
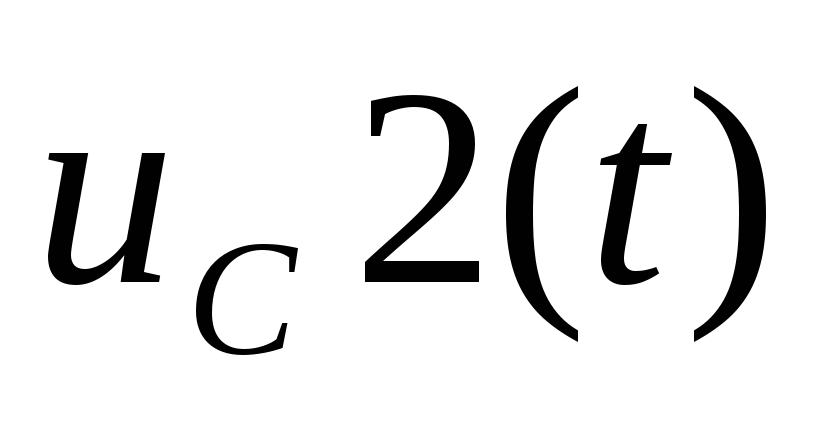
в) г)

Рис. 4.4. RC – цепь и ее резистивная форма.

Для получения значений а и b необходимо, согласно правилам, оп­ределить резистивную форму цепи. С этой целью выберем направление тока I_{C ,} генерируемого источником, и заменим емкость источником ЭДС. Направление ЭДС этого источника должно быть встречным току I_С. Ис­пользование источника ЭДС вместо емкости в момент замыкания ключа t =0₊ обосновывается тем, что напряжение на емкости, согласно второму закону коммутации, не может изменяться скачком. В момент замыкания ключа k в цепи устанавливается максимальный ток (при условии, если ).

Резистивная форма RС-цепи приведена на рис. (4.4 б). Левая часть (4.22) имеет размерность тока. Поэтому, переходя от дифференциального уравнения к алгебраическому, для резистивной цепи (рис. 4.4 б) мы получим:

(4.23)

Для определения коэффициентов а и b будем поочередно варьиро­вать одну из двух переменных, оставляя другую без изменения. Предпо­ложим, что

.

Коэффициент а определяет, во сколько раз изменится ток через емкость, если напряжение на емкости изменится на одну единицу (например, 1 Вольт). Знак коэффициента будем принимать отрицательным, если под действием напряжения будет генерироваться ток, направленный встречно току I_С .

При совпадении направлений генерируемого тока через емкость и тока I_C соответствующий коэффициент будем записывать со знаком «+».

Согласно обозначениям, используемым на рис. (4.4 в), приращение тока по модулю равно:

Так как направление тока является встречным относительно I_С , знак коэффициента должен быть «-», то есть .

Рассмотрим цепь, представленную на рис. (4.4 г), где источник ЭДС исключен, но в цепи содержится его внутреннее сопротивление, равное нулю. Под действием в цепи возникает ток .

Поскольку этот ток совпадает по направлению с током I_С , знак ко­эффициента b, устанавливающего соотношение между и , должен быть «+», то есть:

.

Коэффициент .

Динамическая модель цепи (1.3-10) принимает вид:

,

и для переменной состояния U_С (t) мы получаем стандартную форму запи­си:

(4.24)