3.4. Режим биений
Сложение гармонических колебаний одинаковой частоты и одинакового направления дает гармоническое колебание той же частоты. Амплитуда результирующего колебания равна векторной сумме амплитуд составляющих колебаний.
При сложении двух
гармонических колебаний одного
направления, но различных частот
и
,
векторная сумма амплитуд колебаний
изменяется в функции времени, так как
векторы первого и второго колебаний
вращаются с разными угловыми скоростями.
Если частоты
и
мало различаются между собой, то вектора
относительно друг друга расходятся
весьма медленно, и результирующее
движение рассматривается как синусоидальное
колебание с периодически изменяющейся
амплитудой – биение.
При сложении нескольких гармонических колебаний различных частот получается периодическое движение, период которого является наименьшим кратным периодов составляющих гармонических колебаний.
Режимы биений часто встречаются на практике при включении судовых синхронных генераторов на параллельную работу. Эти режимы подробно рассмотрены в трудах профессора, д.т.н. Константинова В.Н. В его работах, в частности, анализируются энергетические процессы в судовых электроэнергетических установках при отступлениях от идеальных условий синхронизации генераторных агрегатов [10].
Известно, что уравнительный ток синхронизации генераторов (в момент включения) определяется геометрической разностью напряжений или ЭДС генераторов и сопротивлениями цепи. Эта разность изменяется во времени в зависимости от разности угловых скоростей генераторов.
Предположим, что судовая электростанция состоит из двух синхронных генераторов, которые могут включаться на параллельную работу. Напряжение первого генератора изменяется по закону:
,
а второго –
,
где
,
– амплитуды сигналов,
и
– частоты,
– время.
Тогда мгновенные значения разностей напряжений будут равны:
(3.0)
При равенстве
амплитуд напряжений
уравнение (3.30) можно записать:
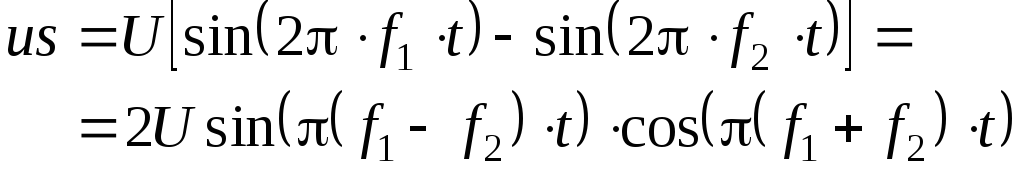(3.0)
Напряжение
называется напряжением биений. Для
выполнения расчетов воспользуемся
простой программой (файл
).
Предположим, что частота первого
генератора
(Гц), а второго
(Гц).
Амплитуды напряжений
(В).
Для построения
графиков определим
и
во временном диапазоне
(с) с шагом дискретности
(с). Затем по формуле (3.30) рассчитаем
напряжение биений
и огибающую напряжения биений, которая
равна:
(3.0)
При построении
графиков воспользуемся оператором
и разместим два синусоидальных сигнала
и
в верхней половине экрана дисплея, а
напряжение биений – в нижней половине.
Напряжение огибающей
и симметричной ей (относительно оси
абсцисс) кривой –
нанесем в виде точек. Этот тип линии
задан с помощью точки, помещенной в
апострофах в последней строке программы.
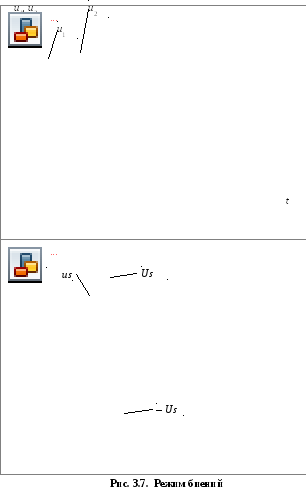
Скопированные с экрана дисплея графики представлены на рис. 3.7.
На графиках четко
видны моменты совпадения синхронизируемых
напряжений по фазе, соответствующие
.
Если
,
форма огибающей существенно изменяется.
В этом можно убедиться, если внести
соответствующие изменения в исходные
данные (девятая строка программы), либо
выполнить расчеты в режиме прямых
вычислений. В качестве упражнения
рекомендуем также убедиться в эффективности
формулы (3.31)
Файл
% Файл "Sah126.m".
% Напряжение биений при синхронизации судовых генераторов.
% u1=U1*sin(w1*t); u2=U2*sin(w2*t)
% Напряжение биений: us=u1-u2;
% Расчет и построение характеристик:
f1 = 50; f2 = 40;
w1 = 2*pi*f1; w2 = 2*pi*f2;
U1 = 230*sqrt (2); U2 = 230*sqrt (2);
% +++++++++++++++++++++++++++++++++++++++++++++++
t = 0:1.0E-003:0.2;
u1 = U1*sin(w1*t); u2 = U2*sin(w2*t);
us = u1-u2;
% Уравнение огибающей:
Us = 2*U1*sin ((w1-w2)*t/2);
Subplot (211)
plot(t, u1, t, u2), grid
pause,
Subplot (212)
plot(t, us, t, Us, '.', t, -Us, '.'), grid
t
