0. 3.4. Резонанс в электрических цепях

Рассмотрим пассивный двухполюсник, подключенный к источнику переменной ЭДС. Двухполюсник содержит одну или несколько индуктивностей и емкостей, а также активные сопротивления. Резонансный режим двухполюсника есть режим, при котором входное сопротивление на резонансной частоте является чисто активным.

П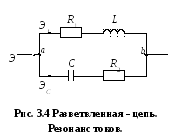ри параллельном соединении ветвей, содержащих и , на резонансной частоте в цепи наблюдается резонанс токов, а при последовательном соединении – резонанс напряжений.

Рассмотрим двухполюсник, изображенный на рис. 3.4. Комплекс тока первой ветви равен току через индуктивность , а второй – равен току через емкость . В неразветвленной части цепи ток равен:

, (3.0)

где , , ,

,

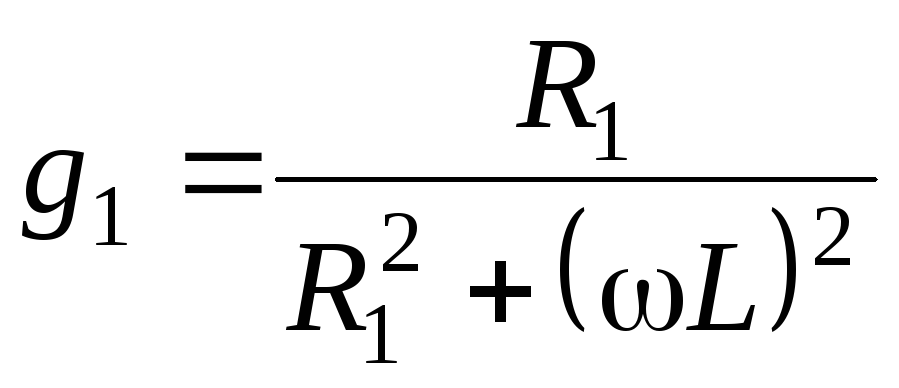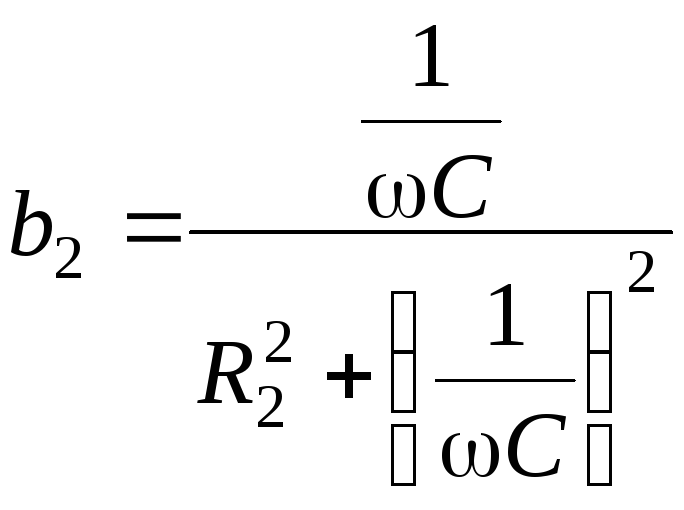– комплексное напряжение между узлами и (рис. 3.4).

Символом обозначено число .

Резонанс токов в цепи (рис. 3.4) может быть достигнут путем изменения , , или и , то есть изменения частоты, индуктивности, емкости, либо активных сопротивлений. Из (3.20) следует, что ток является геометрической суммой токов ветвей и . Вектор тока отстает по фазе от вектора напряжения , а вектор – опережает . В режиме, отличающемся от резонансного, вектора и не совпадают по фазе. В резонансном режиме мнимая часть комплексной проводимости в формуле (3.20) равна нулю: . Следовательно, резонанс токов в цепи (рис. 3.4) наступает при выполнении условия:

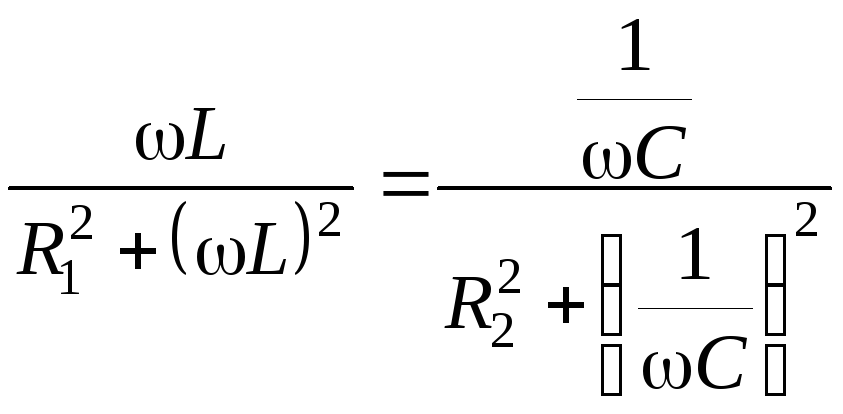(3.0)

В резонансном режиме вектора и совпадают по фазе.

При нахождении или по формуле (3.21) можно для искомой величины получить одно или два действительных значения, либо одно мнимое. В первом случае в цепи могут наблюдаться два резонансных режима. Во втором, характеризуемом мнимыми расчетными значениями или , резонанс невозможен.

В простейшем случае, когда , резонанс наступит при условии:

(3.0)

Если и можно допустить , то резонансная частота:

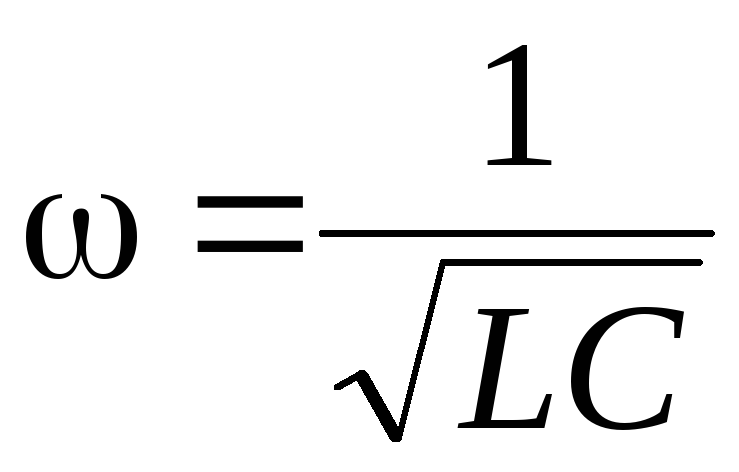(3.0)

В резонансном режиме ток , потребляемый от источника электроэнергии, является минимальным. Он может быть значительно меньше, чем ток в ветвях электрической цепи. Если допустить и (условие практически невыполнимое), то для резонанса будет характерно то, что проводимость цепи должна быть близка к нулю. Это означает возрастание (почти до бесконечности) входного сопротивления на клеммах и уменьшение до ничтожно малой величины по сравнению с и .

П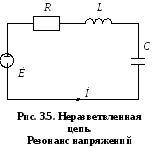ри последовательном соединении , и в электрической цепи, приведенной на рис. 3.5, может наблюдаться резонанс напряжений.

Комплексное сопротивление цепи (рис. 3.5):

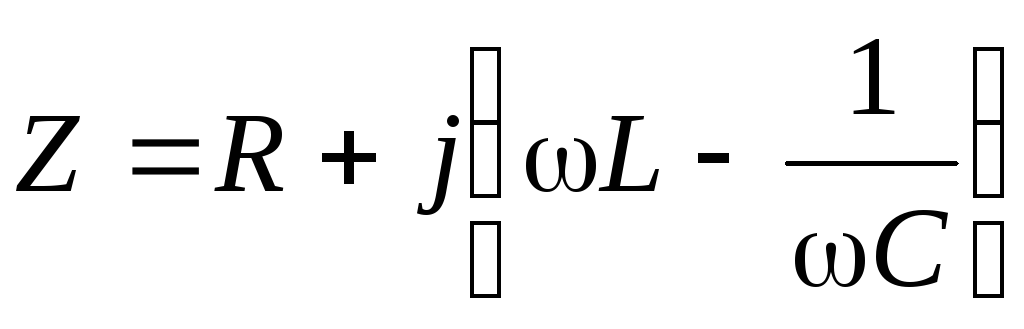
В зависимости от значения мнимой составляющей сопротивления цепи, вектор тока будет либо отставать по фазе от вектора напряжения (индуктивный характер нагрузки), либо опережать его (емкостной характер нагрузки).

В резонансном режиме и совпадают по фазе, так как:

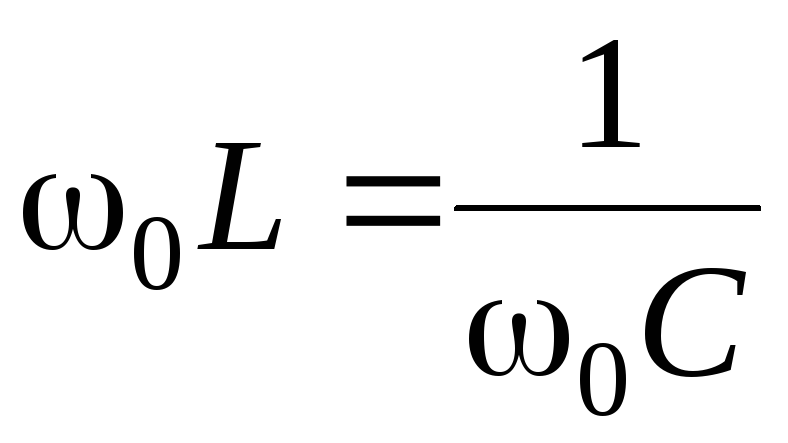(3.0)

Поскольку на частоте входное сопротивление цепи , действующее значение тока в цепи стремится к максимуму:

(3.0)

При выполнении условий (3.24) и (3.25), согласно второму закону Кирхгофа, напряжение на емкости должно быть равно напряжению на индуктивности:

(3.0)

Величину

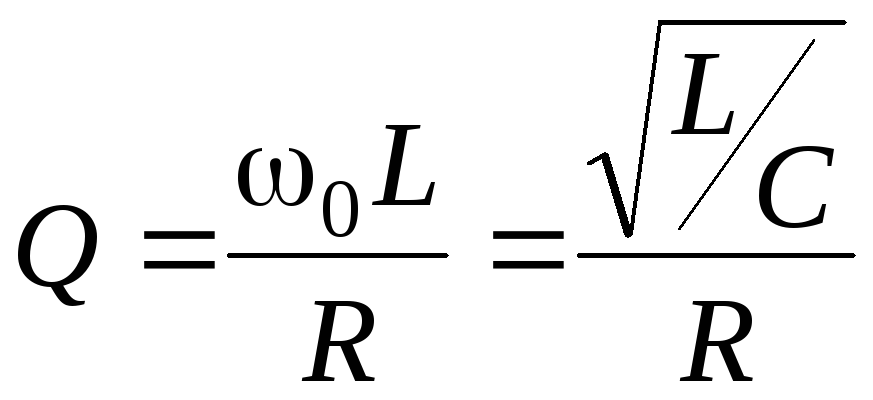(3.0)

называют добротностью резонансного контура. Добротность показывает, во сколько раз (в резонансном режиме) напряжение на индуктивности (емкости) превышает напряжение источника питания цепи . Например, добротность резонансных контуров различных радиотехнических устройств может превосходить 300-350.

Для моделирования резонансного режима в среде MatLAB используем электрическую цепь (рис. 3.5). Предположим, что параметры , , – постоянны. ЭДС источника имеет неизменную амплитуду. Частоту же этой ЭДС будем изменять, и исследуем установившиеся режимы.

Ток в цепи:

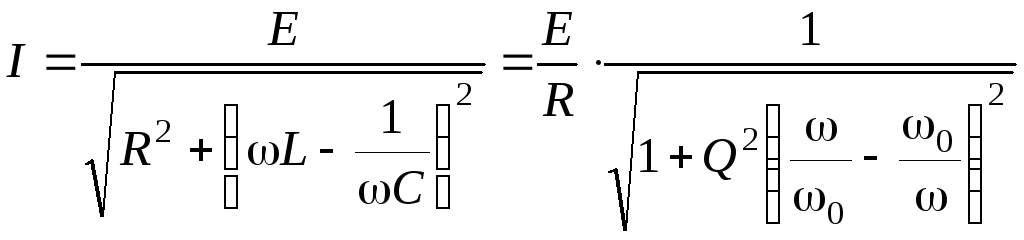, (3.0)

где – резонансная частота.

Для выполнения расчетов и графических построений по формуле (3.28) выразим ток в относительных единицах, приняв за базовое значение ток в резонансном режиме. В результате (3.28) преобразуется к виду:

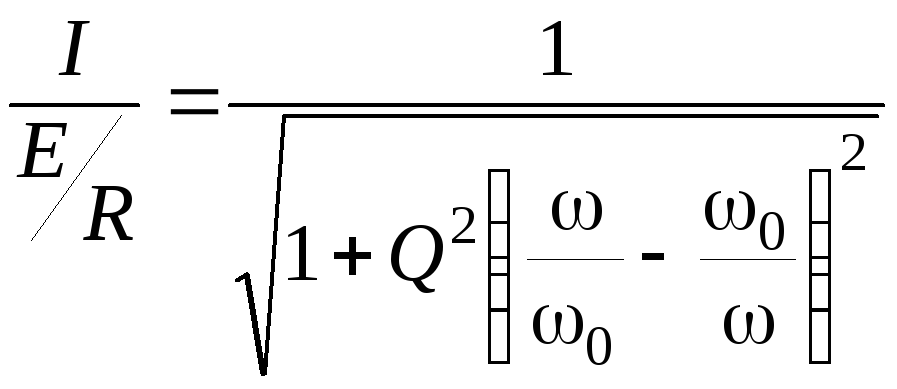(3.0)

Вычисления по формуле (3.29) и построение резонансных кривых выполнены во второй части программы, помещенной в файле после комментария «%Electrical circuits». Вторая часть программы аналогична первой и содержит фактически те же операторы. Формула (3.29) отличается от (3.18). Она содержит в знаменателе как относительную частоту , так и переменную , обратную ей. Поэтому, чтобы исключить в процессе вычислений деления на нуль, диапазон изменения относительной частоты выбран . Введен также новый масштаб переменных по оси абсцисс и ординат (вектор ). Для записи тока цепи

в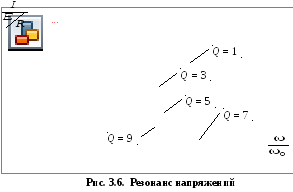 относительных единицах использован идентификатор , а формирование вектора данных во внутреннем цикле из элементов осуществлено путем наполнения . Расчеты во внутреннем цикле выпо4лнены с шагом дискретности , а во внешнем варьируется добротность в диапазоне с шагом дискретности . Таким образом, в результате вычислений получены пять кривых, которые приведены на рис. 3.6. По окончании вычислений отменен режим наложения графиков и осуществлен возврат к автомасштабированию.