3.2.Резонанс в динамических системах

Расчет колебаний в динамических системах и сложных механических конструкциях часто выполняется с целью определения опасных для прочности деталей машин и узлов колебаний (вибраций) и установления способов их ослабления, либо устранения.

Опасным колебательным режимом является резонанс, характеризуемый резким увеличением амплитуды колебаний при совпадении частот собственных колебаний с частотой изменения внешних сил.

Простейшая колебательная система изображена на рис 3.2. Предположим, что движение массы совершается только по вертикальной оси. Масса прикреплена к пружине (упругому элементу), обладающей жесткостью . Геометрическое положение системы определяется только одной координатой , то есть является системой с одной степенью свободы.

При отклонении массы на расстояние от положения равновесия упругий элемент создает восстанавливающую силу: .

Движение массы при отсутствии рассеяния энергии представляет гармоническое колебание:

(3.0)

где – время, – частота собственных колебаний, которая при отсутствии рассеяния энергии равна:

(3.0)

Амплитуда свободных колебаний определяется по формуле:

(3.0)

где – начальное перемещение тела, – начальная скорость.

Фазовый угол

(3.0)

Полный запас энергии в системе равен сумме потенциальной и кинетической энергии: , где и . Свободные колебания совершаются без рассеяния энергии, а также при отсутствии ее пополнения от внешнего источника:

(3.0)

Предположим теперь, что при движении тела сила сопротивления не равна нулю (пропорциональна скорости). Тогда перемещение тела во времени можно вычислить по формуле:

(3.0)

В системе с затуханием колебаний (3.15) частота собственных колебаний равна:

, (3.0)

где 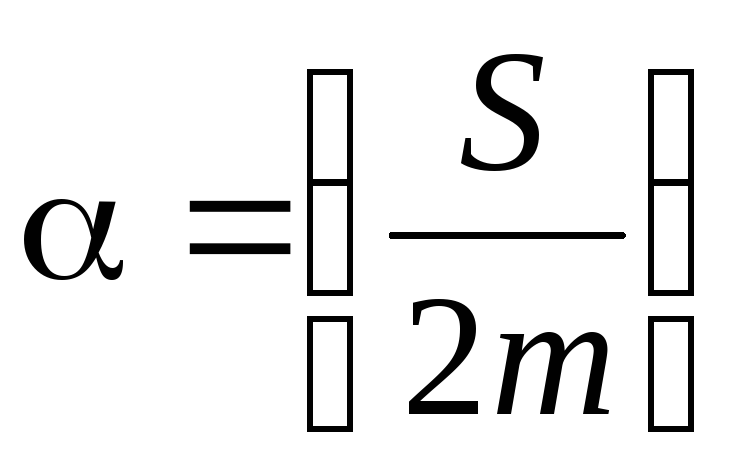. Здесь – сила сопротивления, отнесенная к единице скорости. При очень большом затухании движение становится апериодическим, то есть теряет колебательный характер.

Если на массу воздействовать внешней силой , то движение тела определится по формуле:

(3.0)

Правая часть уравнения (3.17) состоит из двух слагаемых. Первое слагаемое представляет затухающие свободные колебания, где амплитуда и фаза определяются из начальных условий. Второе слагаемое определяет вынужденные колебания, имеющие частоту внешней силы. С увеличением времени первое слагаемое, содержащее экспоненциальный член, уменьшается и через несколько периодов становится практически равным нулю. Вынужденные колебания продолжаются в течение всего времени действия внешней силы. Поэтому при изучении вынужденных колебаний можно принимать лишь второе слагаемое.

Амплитуда вынужденных колебаний определяется по формуле:

(3.0)

Отношение называется коэффициентом динамичности системы или коэффициентом динамического усиления. Величина есть перемещение от статической силы, равной амплитуде гармонической силы :

(3.0)

Коэффициент есть коэффициент демпфирования. Из формулы (3.18) следует, что является функцией двух переменных: и . Поэтому для исследования зависимости коэффициента динамического усиления от указанных переменных произведем необходимые вычисления и построим соответствующие графики.

Остановимся кратко на описании программы, составленной для этих целей в среде MatLAB и содержащейся в файле . Программа состоит из двух частей, позволяющих исследовать резонансные явления в механической системе и электрической цепи. Если подходить к резонансному режиму с позиций динамических аналогий, существующих между элементами электрической цепи и механической системы, то следовало бы иметь одну часть программы. Однако вторая часть, следующая после комментария «Electrical circuits», введена для удобства анализа, поскольку при описании резонансных явлений в электрических цепях использованы обозначения и формулы, определяемые спецификой изложения материала в соответствующих учебных курсах.

Файл

%File 'sah33.m'

%Resonance.

%Mechanical system.

clg;

MV=[0, 2.5, 0, 5.0];

axis(MV)

plot(2.5, 5.0)

hold on;

for gam=0:0.1:0.5;

clear w;

lam1=[];

for w=0:0.01:2.5;

lam=1/(sqrt((1-w^2)^2+(gam^2)*(w^2)));

lam1=[lam1;lam];

end;

w=0:0.01:2.5;

plot(w, lam1), grid,

end;

pause,

hold off;

axis('normal');

%Electrical circuits.

clg;

M1V1=[0, 2.5, 0, 1.0];

plot(2.5, 1.0), axis(M1V1)

hold on;

for q=1.0:2:9;

clear w1;

lam2=[];

for w1=0.01:0.01:2.5;

lam3=1/(sqrt(1+(q^2)*((w1-1/w1)^2)));

lam2=[lam2; lam3];

end;

w1=0.01:0.01:2.5;

plot(w1, lam2), grid,

end;

pause

hold off

axis('normal');

Первые три строки программы содержат комментарии. С помощью оператора очищается графический экран. Затем вводится вектор , с помощью которого путем использования оператора задается масштаб по оси абсцисс и ординат. Первый элемент вектора – минимальное значение , второй – максимальное значение , третий – минимальное значение , четвертый – его максимальное значение. Оператор обеспечивает нанесение числовых данных на оси абсцисс и ординат.

Р езультаты вычислений по формуле (3.18) изобразим в виде графиков на плоскости. Каждый график представляет собой зависимость от переменной при заданном (фиксированном значении ). С помощью оператора в девятой строке мы зададим построение шести графиков с фиксированным от 0 до 0,5 с шагом дискретности 0,1. Цикл начинается с девятой строки и завершается восемнадцатой строкой (оператором ). Назовем этот цикл внешним. Во внешнем цикле содержится внутренний цикл (начало- оператор в двенадцатой строке, завершение – оператор в строке 15). Во внутреннем цикле для каждого фиксированного , определяемого внешним циклом, производятся вычисления по формуле (3.18) (формула набрана в строке 13) при изменении от 0 до 2,5 с шагом дискретности 0,01. Чтобы построить график, нам необходимо образовать вектор-строку из расчетных данных. С этой целью в строке 11 программы введем «пустой» вектор , который будет увеличиваться на один элемент после выполнения одного внутреннего цикла вычислений. Формирование вектора обеспечивается оператором в строке 14. По завершении расчетов во внутреннем цикле и окончании формирования вектора нам необходимо построить график по вычисленным значениям элементов вектора. Построение графика и нанесение масштабной сетки производится операторами и в 17 строке (внешний цикл).

Чтобы построить графики шести кривых на одной и той же плоскости, необходимо в графическом окне сохранить предшествующие построения, исключить возможность их стирания. Режим наложения графиков друг на друга задается командой (восьмая строка программы), а отменяется по окончании построений командой (двадцатая строка). Наконец, программа завершается выполнением оператора , осуществляющего возврат к автоматическому масштабированию.

Результаты вычислений зависимости от отношения частоты возбуждения к собственной частоте для постоянных , выполненные по программе , представлены на рис. 3.3.