2.5. Модель твердого тела с двумя неподвижными точками
Классические модели статики твердых тел и механических конструкций при воздействии на них произвольной системы сил хорошо известны из курса теоретической механики. Их построение базируется на пяти аксиомах статики и системе правил, определяющих необходимые и достоверные условия равновесия сил в пространстве относительно выбранной системы координат.
В общем случае для равновесия системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы сумма проекций всех этих сил на каждую из трех произвольно выбранных координатных осей равнялась нулю и чтобы сумма их моментов относительно каждой из этих осей также равнялась нулю.
Получив систему уравнений, отвечающую условиям равновесия, мы можем представить ее в векторно-матричной форме и решить в среде MatLAB.
Рассмотрим следующую задачу.
На горизонтальном
валу трансмиссии (рис. 2.11) находятся два
жестко соединенных с ним шкива. Радиусы
большого и малого шкивов, соответственно,
равны
и
.
Известны силы натяжения ветвей ремня,
охватывающего передний шкив,
и
.
Сила
вертикальна, а сила
,
как следует из рис. 2.11 б), образует с
вертикалью угол
.
Натяжения ветвей ремня, охватывающего
второй шкив, равны
и
,
причем силы
и
параллельны и образуют с вертикалью
угол
.
Необходимо
определить реакции подшипников
и
,
перпендикулярные к оси вращения вала,
и модули сил
и
,
при условии, что
.
Реакции подшипников и силы
,
,
,
уравновешиваются (вал вращается
равномерно). Расстояние между шкивами
и расстояния шкивов от подшипников
приведены на рис. 2.3 а). Весом вала и
шкивов пренебрегаем.
Решение задачи
начнем с выбора начала координат (точки
)
и направления осей
,
,
.
Силы
,
,
,
перпендикулярны оси
.
Cоставляющие по осям
и
реакций подшипников в точках
и
обозначим, соответственно, через
,
и
,
.
Таким образом, определению подлежат
шесть неизвестных:
,
,
,
,
,
.
Для их нахождения необходимо составить
шесть уравнений: пять уравнений равновесия
и шестое уравнение – соотношение
,
данное в условии задачи. Заметим, что
все силы перпендикулярны к оси
;
их проекции на эту ось равны нулю. Поэтому
уравнение проекций на ось
не составляется. Проекции сил на оси
и
представим в виде уравнений:
Рис. 2.11. Схема трансмиссии
(0.0)
(0.0)
Составим уравнения
моментов всех сил относительно каждой
из координатных осей. Моменты сил,
приложенных в точках
и
,
относительно оси
равны нулю, так как линии действия этих
сил пересекают ось. Рассмотрим рис. 2.3
б). Чтобы получить моменты сил
,
,
,
относительно оси
,
достаточно модуль каждой из этих сил
умножить на радиус соответствующего
шкива и взять их произведения с
соответствующим знаком:
(2.0)
Моменты сил
относительно оси
определим по формуле:
(2.0)
Моменты сил
относительно оси
:
(2.0)
|
Исходные данные: |
|
|
|
|
|
|
|
|
Введем вектор
искомых переменных:
После подстановки
исходных данных в формулы (2.492.53),
с учетом равенства
,
получим систему уравнений:
.
Модель трансмиссии в векторно-матричной форме имеет вид:
, (2.0)
где
,
.
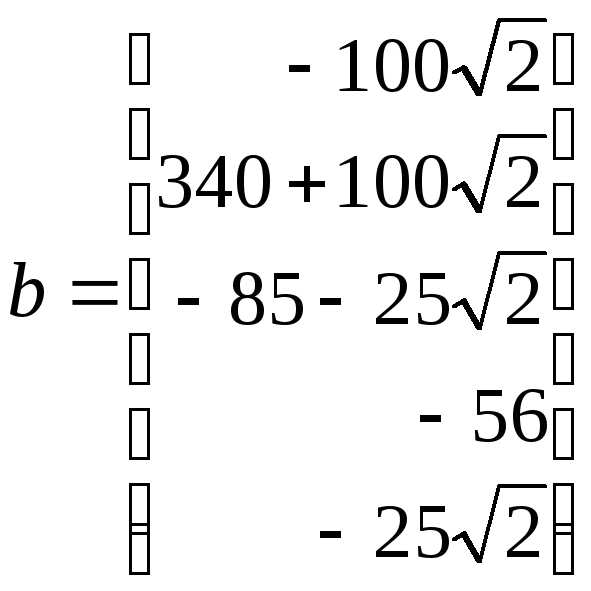Для решения системы (2.54) составим простую программу, приведенную ниже.
Файл
%File ‘sah21.m’. example from theoretical mechanics.
A= [1 1 0 0 1.5
0 0 1 1 –1.5*sqrt(3)
0 0 0 –1.5 1.5* sqrt(3)
0 0 0 0 –0.2
0 1.5 0 0 1.5]
pause,
B=[–100*sqrt(2); 340+100*sqrt(2); –85–25*sqrt(2); –56; –25*sqrt(2)]
pause
C=inv(A)
pause
X=C*B
Решение задачи, выполненное на компьютере в среде MatLAB, выведено на печать с экрана дисплея путем нажатия клавиши <Print Screen>.
Здесь вектор
,
матрица
,
в чем легко убедиться, если умножить
на
.
Рассмотренная задача может быть решена в режиме прямых вычислений. С этой целью, в порядке упражнения, выполните операции, предусмотренные приведенной программой.
п sah21
A =
1.0000 1.0000 0 0 1.5000
0 0 1.0000 1.0000 –2.5981
0 0 0 –1.5000 2.5981
0 0 0 0 –0.2000
0 1.5000 0 0 1.5000
B =
–141.4214
481.4214
–120.3553
–56.0000
–35.3553
C =
1.0000 0 0 2.5000 –0.6667
0 0 0 5.0000 0.6667
0 1.0000 0.6667 –4.3301 0
0 0 –0.6667 –8.6603 0
0 0 0 –5.0000 0
X =
–257.8511
–303.5702
643.6716
565.2111
280.0000
п